Materi tutorialuts kaled3warna

3 Turunan
3.1 De nisi Turunan
1. Rumus de nisi turunan:
Turunan di suatu bilangan/titik tertentu
f0
(a)=lim
x!a
f (x) f (a)
x a
atau
f0
(a)=lim
h!0
f (a + h) f (a)
h
;
dengan a suatu bilangan tertentu dan asalkan limitnya ada.
Turunan sebagai fungsi
f0
(x)=lim
p!x
f (p) f (x)
p x
; atau
f0
(x)=lim
h!0
f (x + h) f (x)
h
;
asalkan limitnya ada.
2. Persamaan garis singgung
Persamaan garis singgung dari kurva y = f (x) di x = a adalah
y f (a) = f0
(a) (x a).
3. Kaitan Turunan dengan kekontinuan
"Jika f0
(a) ada, maka f kontinu di a"
yang ekuivalen dengan
"Jika f tidak kontinu di a, maka f0
(a) tidak ada".
3.1.1 Contoh
1. Diketahui fungsi f dengan f(x) = x x2
. Dengan menggunakan de nisi
turunan, tentukan f0
(1).
Jawab:

3.1 De nisi Turunan 3 TURUNAN
Cara 1:
f0
(1) = lim
x!1
f (x) f (1)
x 1
= lim
x!1
(x x2
) 0
x 1
= lim
x!1
x (x 1)
x 1
= lim
x!1
( x) = 1
Cara 2: (pilih salah satu)
f0
(1) = lim
h!0
f (1 + h) f (1)
h
= lim
h!0
[(1 + h) (1 + h)2
] 0
h
= lim
h!0
1 + h (1 + 2h + h2
)
h
= lim
h!0
1 + h 1 2h h2
h
= lim
h!0
h h2
h
= lim
h!0
h ( 1 h)
h
= lim
h!0
( 1 h) = 1 0 = 1:
2. Dengan menggunakan de nisi turunan tentukan f0
(x) bila f (x) =
5x + 3:
Jawab: Misalkan f (x) = 5x + 3; maka
f0
(x) = lim
p!x
f (p) f (x)
p x
= lim
p!x
(5p + 3) (5x + 3)
p x
= lim
p!x
5p + 3 5x 3
p x
= lim
p!x
5 (p x)
p x
= lim
p!x
5
= 5:
Tutorial Kalkulus (UTS) Edisi 3 2 Farida Hanum 2009

Dengan rumus satunya (pilih salah satu)
f0
(x) = lim
h!0
f (x + h) f (x)
h
= lim
h!0
[5 (x + h) + 3] (5x + 3)
h
= lim
h!0
5x + 5h + 3 5x 3
h
= lim
h!0
5h
h
= lim
h!0
5
= 5:
3. Misalkan diberikan fungsi
f (x) =
x + 1; x 1
x 1; x < 1
Dengan menggunakan de nisi turunan, periksa apakah f0
( 1) ada.
Jawab:
Misalkan diberikan fungsi
f (x) =
x + 1; x 1
x 1; x < 1
Turunan dari arah kiri (turunan kiri)
f
0
( 1) = lim
x! 1
f (x) f ( 1)
x ( 1)
= lim
x! 1
x 1 0
x + 1
= lim
x! 1
(x + 1)
x + 1
= 1:
Turunan dari arah kanan (turunan kanan)
f
0
+ ( 1) = lim
x! 1+
f (x) f ( 1)
x ( 1)
= lim
x! 1+
x + 1 0
x + 1
= 1:
Karena lim
x! 1
f (x) f ( 1)
x ( 1)
6= lim
x! 1+
f (x) f ( 1)
x ( 1)
; maka f0
( 1)
tidak ada.
4. Tentukan konstanta a dan b agar f terdiferensialkan di x = 5; dengan
f (x) =
2x + a; x 5
x2
bx; x > 5
:

Jawab:
f (x) =
2x + a; x 5
x2
bx; x > 5
:
Jika f tidak kontinu di x = 5; maka f0
(5) tidak ada. Jadi haruslah f
kontinu di x = 5: Berarti
lim
x!5
f (x) = lim
x!5+
f (x) = f (5)
lim
x!5
(2x + a) = lim
x!5+
x2
bx = 10 + a
10 + a = 25 5b = 10 + a
10 + a = 25 5b (1)
Turunan dari arah kiri
lim
x!5
f (x) f (5)
x 5
= lim
x!5
(2x + a) (10 + a)
x 5
= lim
x!5
2 (x 5)
x 5
= 2:
Turunan dari arah kanan
lim
x!5+
f (x) f (5)
x 5
= lim
x!5+
(x2
bx) (10 + a)
x 5
= lim
x!5+
(x2
bx) (25 5b)
x 5
(dari Pers. (1))
= lim
x!5+
x2
25 bx + 5b
x 5
= lim
x!5+
(x 5) (x + 5) b (x 5)
x 5
= lim
x!5+
(x 5) (x + 5 b)
x 5
= lim
x!5+
(x + 5 b)
= 10 b:
Agar f0
(5) ada, maka haruslah
2 = 10 b ) b = 8
Dari Persamaan (1) diperoleh
10 + a = 25 5 (8)
a = 15 10 = 25:
3.1.2 Soal Latihan
1. Dengan menggunakan de nisi turunan, tentukan f0
(1) untuk
(a) f (x) = 5x 4
(b) f (x) = x2
+ 2x

(c) f (x) = 5
(d) f (x) =
p
x + 3
2. Tentukan pers. garis singgung kurva y = f (x) pada soal nomor 1 di
x = 1:
3. Tentukan f0
(x) untuk
(a) f (x) = x2
+ 2x 4
(b) f (x) = 2
+ 1
(c) f (x) =
1
x 2
4. Periksa apakah g0
( 1) ; g0
(2) ; dan g0
(4) ada untuk
g (x) =
8
<
:
4; 3 x < 1
5 x2
; 1 x 2
3x2
2; x > 2
5. UTS Kalkulus 1 1995 no. 6
Diketahui fungsi f dengan aturan
f (x) = x jx + 2j :
Gunakan de nisi turunan untuk mencari f0
(x), kemudian tentukan
daerahnya (Df0 ):
6. UTS Kalkulus/Kalkulus 1 tahun 2003 no. 2.
Diberikan fungsi f dengan f (x) = x
2
3 :
(a) Dengan menggunakan de nisi turunan, periksa apakah f mem-
punyai turunan di x = 0:
(b) Tentukan persamaan garis singgung gra k fungsi f di titik (8; 4) :
7. UTS th. 2000 no. 2. Diketahui fungsi
f(x) =
p
x ; 0 < x 1
ax2
+ bx ; x > 1
Tentukan konstanta a dan b agar f0
(1) ada.
Periksa kekontinuan dulu, baru turunan dari arah kiri dan kanan.
8. Tentukan (jika ada) nilai konstanta a dan b agar fungsi
f(x) =
a(x + 3) ; 0 < x 2
x2
bx ; x > 2
mempunyai turunan di x = 2.

3.2 Rumus-rumus Turunan dan Aturan Rantai 3 TURUNAN
9. Misalkan f suatu fungsi yang terde nisi pada < dan xo 2 <. Jika
f0
(xo) ada, periksa apakah fungsi g dengan
g(x) =
f(x) ; x xo
f0
(xo)(x xo) + f(xo) ; x > xo
mempunyai turunan di xo ? Jika g mempunyai turunan di xo, tentukan
g0
(xo).
10. Dengan menggunakan de nisi turunan, tunjukkan bahwa:
(a) Turunan fungsi ganjil adalah fungsi genap.
(b) Turunan fungsi genap adalah fungsi ganjil.
3.2 Rumus-rumus Turunan dan Aturan Rantai
1. Periksa lagi Aturan Pencarian Turunan (termasuk (uv)0
; dan
u
v
0
)
2. Aturan Rantai
Jika y fungsi dari u; dan u fungsi dari x; maka
dy
dx
=
dy
du
du
dx
(notasi Leibniz), atau
dengan notasi fungsi komposisi
(f g)0
(x) = f0
(g (x)) g0
(x)
Soal Latihan:
1. Hitung
dy
dx
untuk
(a) y = 5x7
+ x
1
3 +
4
x
2:
(b) y =
p
x tan x
(c) y = x3=2
4x x4 3
x2
(d) y =
x2
2
x2 + 1
(e) y =
4x2
+ 5
cos x

3.2 Rumus-rumus Turunan dan Aturan Rantai 3 TURUNAN
2. Tentukan f0
(x) untuk fungsi f dengan
f (x) =
x2
+ x ; 1 x 0
x 2 ; 0 < x 4
3. Tentukan turunan fungsi berikut
f (x) = (2x + 1)4
+ sin2
x3
+ 1 :
4. Tentukan
(a)
dy
dx
untuk y = [sin (2x 1)]2
:
(b)
dy
dx
jika y = cos3
( x2
) (UTS 2001 no. 1b.)
(c)
dy
dx
jika y =
p
x sin x
(d)
dy
dx
jika y = sin
2x
x + 1
5. Misalkan f (x) = x2
5x; g (x) =
p
x: Tentukan
(a) (f + g)0
(1)
(b) (fg)0
(1)
(c)
f
g
0
(1)
(d) (f g)0
(1) ;
(e) (g f)0
(1) :
6. Carilah f0
dalam bentuk g0
:
(a) f (x) = x2
g (x)
(b) f (x) = [g (x)]2
(c) f (x) = g (x2
)
(d) f (x) = g (g (x))
7. Misalkan f (x) = x2
2x; g (2) = 1; dan g0
(x) = 3: Tentukan
(a) (f g)0
(2) ;
(b) (g f)0
(2) :
8. Carilah f0
(x) jika diketahui bahwa
d
dx
[f (2x)] = x2
:

3.3 Turunan Implisit dan Turunan Tingkat Tinggi 3 TURUNAN
9. UTS 2002 no. 1: Tentukan persamaan garis singgung dari kurva
f (x) =
2
x2 + 1
di titik (1; 1) :
10. UTS 1997 no. 1.
Diberikan fungsi f(x) =
6
p
x + 6
. Jawablah pertanyaan di bawah ini.
(a) Perlihatkan bahwa titik (3,2) terletak pada gra k f.
(b) Tentukan kemiringan garis singgung kurva pada fungsi f di titik
(3,2).
(c) Tentukan persamaan garis singgung tersebut.
11. UTS 1997 no. 2b. Tentukan turunan pertama dari fungsi di bawah
ini
g(x) =
p
sin(x2)
x
12. UTS 1997 no. 2c: Misalkan g adalah suatu fungsi yang dapat
didiferensialkan, dan g0
(x) =
5
3
p
x2
. Lebih lanjut diketahui bahwa
f(x) = g(x2
+ 1). Tentukanlah f0
(x).
13. UTS 2001 no. 5.
Diketahui f dan g adalah fungsi dari R ke R yang memenuhi
f 0
(x) =
1
x
; dan (f g) (x) = f (g(x)) = x:
Tunjukkan bahwa g0
(x) = g (x) :
14. UTS 2004 no. 6
Diberikan f(x) = jxj dan g(x) = sin(x + ). Jika ada, tentukan
(a) f0
(x).
(b)
d
dx
(f(x) + g(x)).
3.3 Turunan Implisit dan Turunan Tingkat Tinggi
3.3.1 Contoh
1. Tentukan
dy
dx
dari fungsi implisit berikut
x2
y + xy2
= sin x:

Jawab:
d
dx
x2
y + xy2
=
d
dx
(sin x)
2xy + x2 dy
dx
+ 1 y2
+ x 2y
dy
dx
= cos x
x2
+ 2xy
dy
dx
= cos x 2xy y2
dy
dx
=
cos x 2xy y2
x2 + 2xy
2. Tentukan turunan ke n dari fungsi f dengan
f (x) =
1
(2x 5)2 .
Jawab:
f (x) =
1
(2x 5)2 = (2x 5) 2
:
f0
(x) = ( 2) (2x 5) 3
(2)
f00
(x) = ( 2) ( 3) (2x 5) 4
22
f
000
(x) = ( 2) ( 3) ( 4) (2x 5) 5
23
...
f(n)
(x) = ( 1)n
(n + 1)! (2x 5) (n+2)
2n
:
3.3.2 Soal Latihan
1. Tentukan
dy
dx
dari persamaan implisit
(a) 3x2
+ y2
3y = 3:
(b) sin (xy) + x2
= x y
(c)
y
x + 1
3y = tan x
2. Tentukan
dy
dt
dari persamaan implisit:
(a) y2
+ t2
2yt = 3:
(b) ty2
2y = 2:
3. Tentukan
dy
dx
pada titik (1; 1) dari persamaan
sin xy y2
x2
+ 1 = 0:

4. UTS th. 2000 no. 5 Tentukan persamaan garis singgung pada
kurva cos y = 5x2
+ xy2
di titik (0;
2
).
5. UTS tahun 2003 no. 3 Jika sin (y) = x x3
; tentukan
dy
dx
+ 2
dx
dy
6. Misalkan 4x + y2
= 25 dan
dx
dt
= 5: Gunakan aturan rantai dan pen-
diferensialan implisit untuk menentukan
dy
dt
bila y = 3:
7. Misalkan 2 sin x + 4 cos y = 3; dan
dy
dt
= 3: Tentukan
dx
dt
di titik
6
;
3
:
8. Tentukan
dy
dt
jika 8x3
+ 27y3
4xy = 0 dan t3
+ t2
x x3
= 4:
9. Tentukan
dy
dx
dan
d2
y
dx2
dari persamaan implisit
x2
+ xy + y2
= 1:
10. Tentukan
d2
y
dx2
di titik (2; 1) jika 2x2
y 4y3
= 4:
11. Tentukan turunan ke-n atau
dn
y
dxn
atau f(n)
(x) dari
y = f (x) =
4
2x + 1
:
12. Tentukan turunan ke-n dari fungsi f berikut
f(x) = 1 +
b a
x + a
dengan a; b konstanta real.
13. Tentukan turunan ke-n dari fungsi f berikut
f (x) =
p
2x + 1:
14. Tentukan f(2008)
(x) jika
(a) f (x) = sin 3x
(b) f (x) = x3
+ 4x2
1

3.4 Laju yang Terkait 3 TURUNAN
3.4 Laju yang Terkait
Strategi:
1. Baca masalah dengan seksama.
2. gambarkan diagram jika mungkin.
3. Perkenalkan notasi. Berikan lambang kepada semua besaran yang
merupakan fungsi dari waktu.
4. Nyatakan informasi yang diketahui dan laju yang diperlukan dalam
bentuk turunan.
5. Tuliskan persamaan yang mengaitkan beragam besaran dari masalah
tersebut. Jika perlu, gunakan geometri untuk menghilangkan satu
peubah melalui substitusi.
6. Gunakan Aturan Rantai untuk menurunkan kedua ruas persamaan se-
cara implisit terhadap t:
7. Substitusi informasi yang diketahui ke dalam persamaan yang dihasilkan
dan pecahkan untuk laju yang tidak diketahui tersebut.
[Stewart, 1998]
3.4.1 Contoh:
1. Jika bola salju mencair sehingga luas permukaannya menyusut pada
laju 1 cm2
=menit, maka carilah laju berkurangnya garis tengah pada
waktu garis tengah adalah sebesar 10 cm. (Petunjuk: Luas per-
mukaan bola berjari-jari r adalah 4 r2
)
Jawab:
Misalkan
L = luas permukaan bola,
r = jari-jari bola,
p = 2r = garis tengah bola ) r = 1
2
p
Diketahui:
dL
dt
= 1 cm2
=menit (nilai negatif karena luas permukaan-
nya menyusut)
Ditanyakan:
dp
dt
pada saat p = 10 cm.
Persamaan:
L = 4 r2
= 4
p
2
2
= p2

Dengan menurunkan persamaan ini secara implisit terhadap t; diper-
oleh
dL
dt
= 2 p
dp
dt
:
Pada saat p = 10;
1 = 2 (10)
dp
dt
dp
dt
=
1
20
Jadi, garis tengah bola berkurang dengan kecepatan
1
20
cm/menit
(berarti dengan laju
1
20
cm/menit).
Catatan: laju = jkecepatanj
2. Suatu tabung lingkaran tegak (silinder) dipanaskan sehingga tinggi
tabung dan jari-jari lingkaran berubah dengan laju masing-masing sebe-
sar 2 cm/detik. Hitunglah laju perubahan volume tabung tersebut
pada saat tinggi tabung 10 cm dan jari-jari lingkaran 5 cm.
Jawab:
Misalkan
h adalah tinggi tabung pada saat t;
r adalah jari-jari tabung pada saat t;
V adalah volume tabung pada saat t:
Diketahui:
dr
dt
=
dh
dt
= 2 cm/detik
Ditanyakan
dV
dt
pada saat h = 10 cm dan r = 5 cm.
Persamaan yang menghubungkan laju yang ditanyakan dengan laju
yang diketahui:
V = r2
h:
Jika kedua ruas persamaan ini diturunkan secara implisit terhadap t;
diperoleh
dV
dt
= 2r
dr
dt
h + r2 dh
dt
:
Pada saat h = 10 dan r = 5 :
dV
dt
= [2 (5) (2) (10) + 52
(2)]
= 250
Jai laju perubahan volume pada saat tinggi tabung 10 cm dan jari-jari
tabung 5 cm adalah 250 cm/detik.

3.4.2 Soal Latihan
1. Volume kubus bertambah pada laju 10 cm3
/menit. Berapa cepat luas
permukaan bertambah pada waktu panjang sisi 30 cm?
2. Air bocor keluar dari tangki kerucut terbalik pada laju 10.000 cm3
=menit.
Pada saat yang sama air dipompakan ke tangki pada laju konstan.
Tangki mempunyai tinggi 6 m dan garis tengah di bagian atas adalah
4 m. Jika permukaan air naik pada laju 20 cm/menit pada saat tinggi
air 2 m, carilah laju pemompaan air ke tangki.
3. Sebuah tangga yang panjangnya 18 m bersandar pada dinding vertikal
yang tingginya 12 m sehingga ujung atas tangga melewati dinding.
Apabila ujung bawah tangga ditarik mendatar menjauhi dinding den-
gan laju 2 m per detik, tentukan laju berubahnya sudut pada saat
tangga tersebut membentuk sudut 60 terhadap tanah:(Petunjuk:
tan 60 =
p
3; cos 60 = 1
2
; sin 60 = 1
2
p
3:)
4. UTS tahun 2004 no. 4. Beberapa buldoser milik PT TSLB
(Tukang Sulap Lahan Bersejarah) meraung-raung untuk mengeruk dan
meratakan sebuah lapangan olahraga menjadi lahan parkir bus wisata.
Tanah yang dihasilkan kemudian diangkut untuk ditimbun di suatu
lokasi tak jauh dari lapangan tersebut. Timbunan tersebut memben-
tuk kerucut dengan tinggi (h) yang sama dengan jari-jari (r). Vol-
ume timbunan (V ) bertambah dengan laju 4 m3
/menit. Tentukan
berapa laju pertambahan tinggi timbunan ketika jari-jarinya 2 meter.
(V = 1
3
r2
h).
5. Ujian 1 Kalkulus(1) Semester Pendek 2004 no. 6. Tinggi se-
buah segitiga bertambah pada laju 1 cm/menit sedangkan luas segitiga
bertambah dengan laju 2 cm2
/menit. Pada laju berapakah alas segit-
iga berubah pada waktu tinggi segitiga 10 cm dan luas segitiga 100
cm?
6. UTS Kalkulus/Kalkulus1 2005 no. 7. Seorang pria dengan
tinggi 2 meter berjalan dengan laju 1 m/det mendekati sebuah tiang
lampu setinggi 3 meter. Dengan kecepatan berapa panjang bayangan-
nya berubah pada saat dia berjarak 2 meter dari tiang lampu?
7. UTS Kalkulus 1 th. 2001 no. 7. Sebuah tangki berbentuk kotak
dengan alas bujursangkar dengan sisi 60 cm dan tinggi tangki 100 cm
diletakkan di atas drum berbentuk silinder dengan jari-jari 30 cm dan
tinggi 100 cm. Mula-mula tangki tersebut penuh dengan air sedangkan
drum dalam keadaan kosong. Kemudian air di tangki dialirkan ke
dalam drum dengan laju tertentu sehingga laju turunnya tinggi air di
tangki adalah 10 cm/menit. Tentukan laju naiknya tinggi air di dalam
drum pada saat tinggi air di drum 40 cm.

8. (UTS 2007 no. 10) Ketika sedang menyaksikan suatu pameran
kedirgantaraan, Mr. Rate melihat sebuah pesawat tempur (P) melintas
lurus di depannya dengan laju 500 km/jam. Jarak terdekat lintasan
pesawat tersebut terhadap penonton (Mr. Rate, R) adalah 0,5 km
(lihat gambar).
(a) Tentukan laju sudut pandang penonton-pesawat dan garis lurus
yang tegak lurus terhadap lintasan pesawat ( ) terhadap waktu t,
yaitu
d
dt
; sebagai fungsi dari :
(b) Tentukan nilai maksimum dari
d
dt
:

4 Penggunaan Diferensiasi
4.1 Maksimum-minimum Mutlak
1. "Jika f kontinu pada selang tutup [a; b] ; maka f mencapai nilai maksi-
mum mutlak/global f (c) dan nilai minimum mutlak/global f (d) pada
suatu bilangan c dan d dalam [a; b]".
2. Metode selang tutup
(a) Tentukan bilangan kritis dari f; yaitu c dengan f0
(c) = 0 atau
f0
(c) tidak ada.
(b) Tentukan nilai fungsi f di bilangan kritis dan titik-titik ujung
selang.
(c) Tentukan nilai fungsi terbesar dan nilai terkecil.
4.1.1 Contoh
1. Diketahui fungsi f dengan
f (x) =
1
3
x3
2x2
+ 3x:
Tentukan nilai maksimum dan nilai minimum global fungsi f pada
selang [0; 2] :
Jawab:
f (x) =
1
3
x3
2x2
+3x: Karena f fungsi polinom, maka f kontinu pada
selang tutup [0; 2] :
f0
(x) = x2
4x + 3 = (x 1) (x 3) :
f0
(x) = 0 untuk x = 1; x = 3: Karena 3 =2 [0; 2] maka x = 3 bukan
bilangan/titik kritis fungsi f: Dan karena f0
(x) selalu ada pada selang
[0; 2] maka satu-satunya bilangan kritis fungsi f adalah x = 1:
Titik ujung selang: x = 0; x = 2:
x f (x) Keterangan
0 0 nilai minimum global: 0
1
1
3
2 + 3 =
4
3
nilai maksimum global:
4
3
2
8
3
8 + 6 =
2
3

4.2 Maksimum-minimum Lokal 4 PENGGUNAAN DIFERENSIASI
4.1.2 Soal Latihan
1. Tentukan nilai maksimum dan nilai minimum mutlak/global fungsi f
dengan
(a) f (x) = 3x5
5x3
1 pada selang [ 2; 2]
(b) f (x) = x2
+
2
x
pada selang
1
2
; 2
(c) f (x) =
p
9 x2 pada selang [ 1; 2]
(d) f (x) =
x
x2 + 1
pada selang [0; 2] :
(e) f (x) = 6
p
x 3x pada selang [0; 9] (UTS 2002 no. 2)
(f) f(x) = x3
+ 4x pada selang [ 2; 2] (UTS th. 1999 no. 2)
(g) f (x) = sin x + cos x pada selang
h
0;
3
i
:
(h) f (x) = 1
3
x3
2x2
+ 3x pada selang [0; 2] (UTS 2005 no. 3).
2. UTS Kalkulus/Kalk1 Semester Pendek 2004 no. 5.
Periksa apakah fungsi f dengan
f(x) =
1
3
x3 1
2
x2
2x + 1
pada [ 2; 2] mempunyai nilai ekstrim global? Jika ada, tentukan nilai
ekstrim globalnya.
3. UTS 2004 no. 9a Diketahui fungsi f dengan
f (x) =
x2
+ x ; 1 x 0p
x x ; 0 < x 4
Tentukan : nilai maksimum global dan nilai minimum global fungsi f
pada [ 1; 4].
4.2 Maksimum-minimum Lokal
1. Uji Turunan Pertama
Andaikan c bilangan kritis dari fungsi kontinu f:
(a) Jika f0
berubah dari positif ke negatif pada c; maka f mempunyai
maksimum lokal pada c:
(b) Jika f0
berubah dari negatif ke positif pada c; maka f mempunyai
minimum lokal pada c:
(c) Jika f0
tidak berubah tanda pada c, maka f tidak mempunyai
maksimum atau minimum lokal di c:

4.2 Maksimum-minimum Lokal 4 PENGGUNAAN DIFERENSIASI
2. Uji Turunan Kedua (lebih lemah)
Andaikan f00
kontinu dekat c:
(a) Jika f0
(c) = 0 dan f00
(c) > 0; maka f mempunyai minimum lokal
pada c:
(b) Jika f0
(c) = 0 dan f00
(c) < 0; maka f mempunyai maksimum
lokal pada c:
Soal Latihan:
1. Tentukan (jika ada) nilai maksimum dan minimum lokal dari f den-
gan menggunakan Uji Turunan Pertama. Bandingkan hasilnya dengan
menggunakan Uji Turunan Kedua.
(a) f (x) = x5
5x + 3
(b) f (x) = 1 + (x + 1)2
(c) f (t) =
1
t
(d) f ( ) = sin
(e) f (x) = x +
p
1 x
(f) f (x) =
x2
; jika 1 x < 0
2 x2
; jika 0 x 1
2. UTS Kalkulus th. 2001 no. 3.
Diketahui fungsi f dengan
f (x) = x4
4x3
di R:
Tentukan nilai ekstrim lokal fungsi f dan jenisnya.
3. UTS 2004 no. 9b Diketahui fungsi f dengan
f (x) =
x2
+ x ; 1 x 0p
x x ; 0 < x 4
Tentukan nilai maksimum lokal dan nilai minimum lokal fungsi f pada
( 1; 4).

4.3 Sketsa Gra k 4 PENGGUNAAN DIFERENSIASI
4.3 Sketsa Gra k
Persamaan Garis Asimtot
1. Asimtot Tegak:
Garis x = a adalah asimtot tegak gra k fungsi f jika salah satu
dari pernyataan berikut berlaku:
lim
x!a+
f (x) = +1; lim
x!a
f (x) = +1;
lim
x!a+
f (x) = 1; lim
x!a
f (x) = 1:
2. Asimtot Datar:
Garis y = b adalah asimtot datar dari kurva fungsi f jika salah
satu dari pernyataan berikut berlaku:
lim
x!1
f (x) = b; lim
x! 1
f (x) = b:
3. Asimtot Miring:
Garis y = mx + b merupakan asimtot miring dari kurva fungsi f
jika salah satu dari pernyataan berikut berlaku:
lim
x!1
[f (x) (mx + b)] = 0;
lim
x! 1
[f (x) (mx + b)] = 0
Soal Latihan:
1. Tentukan, jika ada, persamaan garis asimtot (datar, tegak, miring)
dari:
(a) y =
x
x + 2
(b) y =
x2
+ 4
x2 4
(c) y =
x3
+ 1
x3 + x
(d) y =
x3
x2 + 3x 10
(e) y =
1 x
1 + x
(f) y =
1
x 1
x
(g) y =
x2
2x + 5

2. UTS Kalkulus/Kalkulus1 2005 no. 6.
Tentukan persamaan garis dari asimtot-asimtot yang ada pada kurva
fungsi
f (x) = x + 1 +
2
x2 4
beserta alasannya.
3. Tentukan limit-limit berikut:
(a) lim
x!1
x
p
x2 + 1
(b) lim
x! 1
x
p
x2 + 1
Langkah-langkah Pembuatan Sketsa Gra k:
Tentukan (jika ada)
1. Daerah asal fungsi
2. Titik potong dengan sumbu koordinat.
3. Turunan pertama: titik/bilangan kritis, naik-turun fungsi, nilai ek-
strim lokal.
4. Turunan kedua: kecekungan fungsi, titik belok.
5. Asimtot: tegak, datar, miring
(sangat membantu jika juga dicari dari kedua arah: kiri-kanan, takhing-
ga dan negatif takhingga)
6. Sketsa:
(a) Buat tabel ringkasan naik,turun, dan kecekungan fungsi
(b) Gambarkan garis asimtot pada bidang gambar
(c) Petakan titik-titik potong dengan sumbu, titik belok, titik ekstrim
lokal beserta "ciri lekuk"nya.
(d) Sketsakan gra k

4.3.1 Contoh
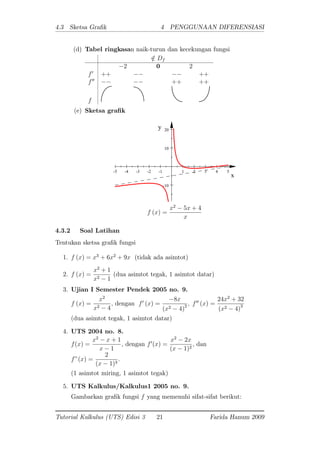
1. Tentukan sketsa gra k fungsi f(x) =
x2
5x + 4
x
:
Df = fxjx 6= 0g
Titik potong dengan sumbu koordinat:
sumbu-x ! y = 0 ! x2
5x + 4 = 0
) (x 4) (x 1) = 0 ) titik pot.: (4; 0) ; (1; 0)
sumbu-y ! x = 0 (tidak ada)
(a) Turunan pertama
f0
(x) =
(x 2) (x + 2)
x2
f0
(x) = 0 untuk x = 2; x = 2; dan f0
(x) tidak ada untuk x = 0:
Tanda f0
(x) + (0) ( ) (0) +
2 0 2
Fungsi f naik pada selang ( 1; 2] dan selang [2; 1); fungsi f
turun pada selang [ 2; 0); dan (0,2]:
Nilai maksimum lokal adalah f ( 2) = ( 2) 5 +
4
2
= 9; nilai
minimum lokal adalah f (2) = 1:
(b) Turunan kedua: f00
(x) =
8
x3
Tanda f00
(x) ( ) + + +
0
Fungsi f cekung ke bawah pada selang ( 1; 0) dan cekung ke
atas pada selang (0; 1) :
(c) Asimtot:
Karena
lim
x!+1
[f (x) (x 5)] = lim
x!+1
4
x
= 0;
maka garis y = x 5 adalah asimtot miring dari fungsi f:
Karena
lim
x!0
f (x) = lim
x!0
x 5 +
4
x
= 1; atau
lim
x!0+
f (x) = +1
maka garis x = 0 merupakan asimtot tegak dari f:
Karena
lim
x!1
f (x) = +1 dan lim
x! 1
f (x) = 1;
maka f tidak mempunyai asimtot datar.

(d) Tabel ringkasan naik-turun dan kecekungan fungsi
=2 Df
2 0 2
f0
++ ++
f00
++ ++
f
(e) Sketsa gra k
-5 -4 -3 -2 -1 1 2 3 4 5
-10
10
20
x
y
f (x) =
x2
5x + 4
x
4.3.2 Soal Latihan
Tentukan sketsa gra k fungsi
1. f (x) = x3
+ 6x2
+ 9x (tidak ada asimtot)
2. f (x) =
x2
+ 1
x2 1
(dua asimtot tegak, 1 asimtot datar)
3. Ujian I Semester Pendek 2005 no. 9.
f (x) =
x2
x2 4
; dengan f0
(x) =
8x
(x2 4)2 ; f00
(x) =
24x2
+ 32
(x2 4)3
(dua asimtot tegak, 1 asimtot datar)
4. UTS 2004 no. 8.
f(x) =
x2
x + 1
x 1
, dengan f0
(x) =
x2
2x
(x 1)2
, dan
f"(x) =
2
(x 1)3
.
(1 asimtot miring, 1 asimtot tegak)
5. UTS Kalkulus/Kalkulus1 2005 no. 9.
Gambarkan gra k fungsi f yang memenuhi sifat-sifat berikut:

4.4 Masalah Pengoptimuman 4 PENGGUNAAN DIFERENSIASI
f kontinu pada ( 1; 0) [ (0; 1) ; f (2) = 3; f ( 2) = 0:
f0
(x) > 0 pada (2; 1) dan f0
(x) < 0 pada ( 1; 0)[(0; 2) ; f0
(2) =
0:
f00
(x) > 0 pada (0; 1) dan f00
(x) < 0 pada ( 1; 0) :
lim
x! 1
f (x) = 2: lim
x!1
[f (x) x] = 0:
lim
x!0
f (x) = 1; lim
x!0+
f (x) = +1:
4.4 Masalah Pengoptimuman
Langkah-langkah Penyelesaian
1. Baca masalah dengan seksama.
2. Gambar diagram, jika memungkinkan.
3. Berikan lambang pada besaran yang harus dimaksimumkan atau di-
minimumkan (misalkan Q): Beri lambang pada besaran takdiketahui
lainnya.
4. Nyatakan Q dalam bentuk beberapa lambang dari Langkah 3.
5. Jika Q merupakan fungsi dari lebih satu peubah, maka nyatakan Q
sebagai fungsi dari satu peubah.
6. Tentukan nilai maksimum atau minimum mutlak/global dari Q:
4.4.1 Contoh
1. Seseorang merencanakan membuat penakar beras dengan bahan lem-
baran logam tipis. Penakar itu berbentuk silinder dengan jari-jari r
dan tinggi h: Misalkan dikehendaki agar volume silinder itu 1 liter
dan ketebalan bahan dapat diabaikan. Bantulah orang tersebut dalam
merancang penakar yang ekonomis dengan cara menjawab pertanyaan-
pertanyaan berikut:
(a) Rumuskan suatu fungsi A (r), dengan A adalah luas bahan yang
digunakan dalam pembuatan silinder yang merupakan fungsi dari
r semata-mata.
(b) Tentukan r dan h yang meminimumkan penggunaan bahan.
(c) Misalkan bahan tersebut terlebih dahulu perlu disemprot kedua
sisinya dengan cairan anti karat. Diketahui biaya penyemprotan
Rp 10/cm2
: Tentukan biaya total minimum untuk penyemprotan
itu.

Jawab:
Misalkan:
r = jari-jari silinder,
h = tinggi silinder,
maka volume silinder adalah
V = r2
h = 1 liter = 1000 cm3
=) h =
1000
r2
:
Misalkan A adalah luas bahan yang digunakan untuk membuat penakar
yang merupakan fungsi dari r; maka
A (r) = 2 rh + r2
= 2 r
1000
r2
+ r2
=
2000
r
+ r2
:
(a) Ukuran silinder (r dan h) yang meminimumkan penggunaan ba-
han dapat diperoleh dari
dA
dr
=
2000
r2
+ 2 r = 0
2 r3
2000
r2
= 0
2 r3
1000 = 0
r3
=
1000
r =
3
r
1000
=
10
1=3
cm.
Jadi
h =
1000
100
2=3
=
10
1=3
cm.
Perhatikan bahwa
d2
A
dr2
=
4000
r3
+ 2 ;
dan
d2
A
dr2
> 0 untuk r =
10
1=3
; sehingga A mencapai minimum lokal
di r =
10
1=3
: Selain itu,
d2
A
dr2
> 0 untuk setiap r > 0; sehingga
A fungsi yang cekung ke atas untuk r > 0: Jadi A mencapai
minimum global/mutlak di r =
10
1=3
:

(b) Biaya penyemprotan Rp 10,00/cm2
; dan bahan harus disemprot
di kedua sisinya. Jadi luas bahan yang disemprot adalah
2
2000
r
+ r2
:
Biaya penyemprotan minimum jika ukuran silinder juga yang mem-
inimumkan biaya pembuatan bahan, yaitu dengan r =
10
1=3
: Jadi
biaya penyemprotan minimum adalah
10 2
2000
10= 1=3
+
100
2=3
= 20 200 1=3
+ 100 1=3
= 6000 1=3
rupiah.
4.4.2 Soal Latihan
1. Carilah dua bilangan positif yang hasil kalinya 100 dan jumlah kedu-
anya bernilai minimum.
2. Carilah dimensi/ukuran persegi panjang dengan keliling 100 m yang
luasnya paling maksimum.
3. Carilah dua bilangan bulat positif sehingga jumlah bilangan pertama
dan empat kali bilangan kedua adalah 1000 dan hasil kali bilangan-
bilangan tersebut sebesar mungkin.
4. Margin atas dan bawah sebuah poster masing-masing 6 cm dan margin
samping masing-masing 4 cm: Jika luas bahan tercetak pada poster
tetap 384 cm2
; carilah dimensi poster dengan luas terkecil.
5. UTS tahun 2003 no. 7 Suatu kotak tertutup berbentuk balok den-
gan volume 400 cm3
mempunyai alas berbentuk persegi (bujur sangkar).
Harga bahan untuk membuat bagian tutup dan bagian alas kotak
adalah 1000,- rupiah per cm2
; sedangkan harga bahan untuk bagian
dinding (samping) adalah 540,- rupiah per cm2
: Tentukan ukuran ko-
tak tersebut agar biaya bahan yang diperlukan minimum.
6. UTS Kalkulus(1) Semester Pendek 2004 no. 9 Sebuah pem-
bangkit tenaga listrik terletak di tepi sebuah "sungai lurus" yang lebarnya
3 km. Sebuah pabrik terletak di seberang sungai 10 km ke arah hilir
dari titik A yang tepat berseberangan langsung dengan pembangkit.
Jalur mana yang paling hemat untuk pemasangan sebuah kabel yang
menghubungkan pembangkit tenaga listrik dengan pabrik jika biaya pe-
masangan kabel di bawah air 2a rupiah per km dan biaya pemasangan
kabel di darat adalah a rupiah per km.
7. UTS Kalkulus/Kalkulus 1 2002 no. 9. Pak Koko memiliki
seekor sapi. Untuk membiayai sekolah anaknya, ia merencanakan un-
tuk menjual sapinya yang saat ini berbobot 100 kilogram. Jika Pak

4.5 Teorema Nilai Rata-rata 4 PENGGUNAAN DIFERENSIASI
Koko menunda penjualan sapinya, maka bobot sapi tersebut bertam-
bah 1 kilogram per hari, tetapi ia harus menanggung biaya pemeli-
haraan Rp 2.000,- per hari. Saat ini harga 1 kilogram sapi adalah
Rp 10.000,- dan harga ini turun Rp 50,- per hari. Berapa harikah Pak
Koko harus menunggu menjual sapinya agar keuntungan yang diperoleh
maksimum. Catatan: yang dimaksud dengan "keuntungan" adalah
pendapatan dikurangi biaya pemeliharaan selama menunda penjualan.
8. UTS tahun 2004 no. 10. Seorang simpatisan partai politik akan
menempel poster partainya pada tembok sebuah gedung tinggi. Pada
jarak 8 meter di depan gedung tersebut terdapat pagar setinggi 1 meter.
Simpatisan tersebut akan membuat tangga yang menghubungkan jalan
di luar pagar dengan tembok tinggi tersebut. Dengan berbekal penge-
tahuan Kalkulus, bantulah simpatisan partai tersebut untuk menen-
tukan panjang minimum tangga tersebut.
9. UTS 1998 no. 10. Pak Hamid adalah seorang nelayan yang tinggal
di sebuah desa yang letaknya di tepi pantai Pulau Batam. Suatu hari
dia diundang oleh seorang temannya yang tinggal di Singapura. Un-
tuk bisa sampai di rumah temannya, dia merencanakan menggunakan
perahu pribadinya sampai di pelabuhan Singapura, kemudian dari sana
perjalanan dilanjutkan dengan menggunakan mobil. Jarak yang ditem-
puh dengan perahu adalah 10 km, sedangkan dengan mobil sejauh 20
km.
Dia akan mengemudikan perahunya dengan kecepatan tetap x km/jam
dengan laju pemakaian bensin
x2
100
liter/jam. Diketahui kecepatan mo-
bil dua kali kecepatan perahu dengan pemakaian bensin satu setengah
kali pemakaian bensin untuk perahu per jamnya. Ongkos sewa mobil
(tanpa bensin) Rp 10000/jam. Jika harga bensin Rp 1000/liter,
(a) rumuskanlah fungsi biaya yang harus dikeluarkan Pak Hamid.
(b) Tentukanlah kecepatan perahu dan taksi yang meminimumkan bi-
aya di atas.
4.5 Teorema Nilai Rata-rata
Teorema Nilai Rata-rata (untuk turunan)
Misalkan f fungsi yang memenuhi hipotesis berikut:
1. f kontinu pada selang tertutup [a; b] ;
2. f terdiferensialkan pada selang terbuka (a; b) ;
maka terdapat bilangan c dalam (a; b) sehingga
f0
(c) =
f (b) f (a)
b a
:

4.5.1 Contoh
1. Diberikan fungsi f dengan f (x) = x2
+ 2x 3 pada selang [0; 2] :
(a) Periksa apakah syarat berlakunya Teorema Nilai Rata-rata (TNR)
terpenuhi.
(b) Gunakan TNR untuk mendapatkan nilai c:
Jawab:
f (x) = x2
+ 2x 3:
(a) Karena f fungsi polinom, maka f kontinu pada selang [0; 2] :
f0
(x) = 2x+2 selalu ada untuk setiap x 2 (0; 2) : Ini berarti f ter-
diferensiabel pada selang (0; 2) : Jadi syarat berlakunya Teorema
Nilai Rata-rata dipenuhi f pada selang [0; 2] :
(b)
f0
(c) =
f (2) f (0)
2 0
2c + 2 =
5 ( 3)
2
= 4
2c = 2
c = 1
4.5.2 Soal Latihan
1. Periksa apakah TNR untuk turunan dapat diterapkan pada fungsi-
fungsi berikut. Jika ya, tentukan nilai c yang dijamin TNR pada selang
yang diberikan
(a) f (x) = x2
7; pada selang [2; 3]
(b) f (x) = x3
x2
x + 1 pada selang [0; 2]
(c) f (x) = sin x pada selang 0; 2
;
(d) f (x) =
1
x
pada selang [1; 3]
(e) f (x) =
1
x
pada selang [ 1; 1] ;
(f) f (x) =
x
x 2
pada selang [ 1; 1]
(g) f (x) =
x
x 2
pada selang [0; 3]
(h) f (x) = x1=3
pada elang [ 1; 1] :
2. Jika f (1) = 10 dan f0
(x) 2 untuk 1 x 4; seberapa kecilkah nilai
f (4) yang mungkin?

3. Jika f (0) = 3 dan f0
(x) 5 untuk semua nilai x; seberapa besarkah
nilai f (2) yang mungkin?
4. Ujian I Kalkulus/Kalkulus 1 Semester Pendek 2005 no. 3.
Diberikan fungsi f dengan f (x) = x2
+ 2x 3 pada selang [0; 2] :
(a) Periksa apakah syarat berlakunya Teorema Nilai Rata-rata (TNR)
terpenuhi.
(b) Gunakan TNR untuk mendapatkan nilai c:
5. UTS th. 1998 no. 3.
Perlihatkan bahwa jika f (x) = x2
+ 2x + 1 pada selang [a; b] ; maka
bilangan c dari Teorema Nilai Rata-rata selalu berupa titik tengah dari
selang tersebut.
6. UTS tahun 2004 no. 5.
Badrun berangkat dari Jakarta ke Cikampek melalui jalan tol berjarak
156 km selama 1.5 jam dengan mengendarai mobil tanpa berhenti.
Sampai di gerbang tol Badrun ditangkap polisi karena kecepatan mo-
bilnya melebihi kecepatan yang diijinkan di jalan tol (maksimum 100
km/jam). Gunakan Teorema Nilai Rata-rata untuk menunjukkan bah-
wa kecepatan mobil Badrun pernah melebihi 100 km/jam.
7. UTS Kalkulus 2001 no. 6.
Periksalah apakah Teorema Nilai Rata-rata dapat diterapkan pada
fungsi dan selang [a; b] yang diberikan berikut ini. Bila dapat, ten-
tukan semua nilai c sehingga f0
(c) =
f (b) f (a)
b a
:
(a) f (x) = x2=3
, pada selang [0; 2] :
(b) g (x) = x +
1
x
, pada selang 1;
1
2
:
8. UTS tahun 2003 no. 10.
Andaikan bahwa fungsi f dan g kontinu pada [a; b] dan terturunkan
pada (a; b) : Andaikan juga f (a) = g (a) dan f0
(x) < g0
(x) untuk
a < x < b: Gunakan Teorema Nilai Rata-rata untuk membuktikan
bahwa f (b) < g (b) :

PUSTAKA PUSTAKA
Pustaka
[1] Stewart, J. 1998. Kalkulus. Jilid 1. Penerjemah: I N. usila & H. Gunawan.
Erlangga, Jakarta. Terjemahan dari Calculus, Fourth Edition.
[2] Hanum, F (ed). 2006. Bank Soal Kalkulus TPB (1995-2005) . Departemen
Matematika FMIPA IPB, Bogor. Tidak dipublikasikan.

Materi tutorialuts kaled3warna

Recommended

Recommended

More Related Content

What's hot

What's hot (20)

Similar to Materi tutorialuts kaled3warna

Similar to Materi tutorialuts kaled3warna (20)

More from IKHTIAR SETIAWAN

More from IKHTIAR SETIAWAN (20)

Recently uploaded

Recently uploaded (20)

Materi tutorialuts kaled3warna