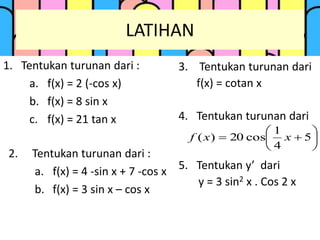
Dokumen tersebut membahas tentang turunan trigonometri, dimulai dengan motivasi dan kompetensi dasar yang dicapai. Berisi penjelasan rumus-rumus dasar turunan fungsi trigonometri dan contoh soal beserta penyelesaiannya. Diakhiri dengan latihan soal untuk mempraktikkan pemahaman tentang turunan trigonometri.

1. Turunan Trigonometri
Rayhan Farisi Ramadhan
Sri Aji Cakraningrum
Stefani Sekar Ananta
KELOMPOK 9
KD 3.3

3. Motivasi

4. Teruslah sebarkan hal positif dan
berkatalah yang baik, karena kita
tidak pernah tau perkataan kita
yang mana yang akan merubah
dunia seseorang

5. Turunan Trigonometri
4.3 Menyelesaikanmasalah
yang berkaitan dengan
turunan fungsi
trigonometri
3.3 Menggunakanprinsip
turunan ke fungsi
trigonometri sederhana
kompetensi dasarKompetensi Dasar

6. Peta konsep
Rumusdasar
Turunan Trigonometridengan
TURUNAN TRIGONOMETRI BERPANGKAT
SUDUT (ax+b)
TURUNAN
TRIGONOMETRI

7. Turunan trigonometri
Turunan dari suatu fungsi pada titik tertentu
menjelaskan sifat-sifat fungsi yang mendekati nilai
input.
Turunan trigonometri adalah persamaan turunan
yang melibatkan fungsi - fungsi trigonometri seperti
sin, cos, tan, cot, sec dan csc

8. Sifat-sifatturunanfungsi trigonometri
Dengan u dan v adalah fungsi yang masing-masing
mempunyai turunan u’ dan v’ serta C adalah skalar
2
'.'.
'.5
'.'.)('..4
'''.3
'''.2
'.'..1
v
vuvu
f
v
u
f
vuvuxfvuf
vufvuf
vufvuf
uCfuCf







9. = lim
ℎ→0
sin 𝑥+ℎ −sin 𝑥
ℎ
= lim
ℎ→0
2 cos
1
2
𝑥+ℎ+𝑥 sin
1
2
(𝑥+ℎ−𝑥)
ℎ
=lim
ℎ→0
2 cos 𝑥+
1
2
ℎ sin
1
2
ℎ
ℎ
=lim
ℎ→0
2 cos 𝑥 +
1
2
ℎ . lim
ℎ→0
𝑠𝑖𝑛
1
2
ℎ
ℎ
=2 cos x .
1
2
= cos x

10. Pembuktian Rumus Turunan Cos X
= lim
ℎ→0
cos 𝑥+ℎ −cos ℎ
ℎ
= lim
ℎ→0
−2 sin
1
2
𝑥+ℎ+𝑥 sin
1
2
(𝑥+ℎ−𝑥)
ℎ
=lim
ℎ→0
−2 sin 𝑥+
1
2
ℎ sin
1
2
ℎ
ℎ
=lim
ℎ→0
[−2 𝑠𝑖𝑛 𝑥 +
1
2
ℎ ] lim
ℎ→0
𝑠𝑖𝑛
1
2
ℎ
ℎ
= - 2 sin x .
1
2
= -sin x

11. y = sin x
y = cos x
y = tan x
y = cot x
y = sec x
y = cosec x
Rumus Dasar
y' = cos x
y' = –sin x
y' = sec2 x
y' = –cosec2 x
y' = sec x . tan x
y' = -cosec x . cot x

12. Contoh
2. Tentukan turunan dari :
f(x) = 4 cos x
Jawab :
f(x) = 4 cos x
f’(x) = 4 (– sin x)
= – 4 sin x
1. Tentukan turunan dari :
f(x) = 7 sin x
Jawab :
f(x) = 7 sin x
f’(x) = 7 cos x

13. Contoh
4. Tentukan turunan dari :
f(x) = 4 sin x – cos x
Jawab :
f(x) = 4 sin x – cos x
f’(x) = 4 cos x – (-sin x)
= 4 cos x + sin x
3. Tentukan turunan dari :
f(x) = 3 sin x + 2 cos x
Jawab :
f(x) = 3 sin x + 2 cos x
f’(x) = 3 cos x + 2 (-sin x)
= 3 cos x – 2 sin x

14. Contoh
6. Tentukan turunan dari :
f(x) = sin x . cos x
Jawab :
misal
u = sin x → u’ = cos x
v = cos x → v’ = - sin x
f(x) = sin x . cos x
f’(x) = u’. v + u. v’
= cos x.cos x + (sin x) (- sin x)
= cos2x – sin2x
5. Tentukan turunan dari :
f(x) = cos x . tan x
Jawab :
xxf
xxf
x
x
xxf
xxxf
cos)('
sin)(
cos
sin
.cos)(
tan.cos)(





15. Turunan TRIGONOMETRI
dengan SUDUT (ax+b)
y = sin (ax+b)
y = cos (ax+b)
y = tan (ax+b)
y = cot (ax+b)
y = sec (ax+b)
y = cosec (ax+b)
y' = a cos (ax+b)
y' = –a sin (ax+b)
y' = a sec2 (ax+b)
y' = –a cosec2 (ax+b)
y' = a sec (ax+b) . tan (ax+b)
y' = -a cosec (ax+b).cot (ax+b)

16. Conto
h1. Tentukan turunan dari :
f(x) = sin (5x – 2)
Jawab :
f(x) = sin (5x – 2)
f’(x) = 5 cos (5x – 2 )
2. Tentukan turunan dari :
Jawab :





















6
5
1
cos)('
6
5
1
cos
5
1
.5)('
6
5
1
sin5)(
xxf
xxf
xxf






 6
5
1
sin5)( xxf

17. Contoh
3. Tentukan turunan dari :
Jawab :
x
x
xf
2
4sin
)( 
2
2
2
2
2
4sin4cos.4
)('
4
4sin24cos.8
)('
)2(
)2(4sin)2.(4cos4
)('
'.'.
)('
2
4sin
)(
x
xxx
xf
x
xxx
xf
x
xxx
xf
v
vuvu
xf
x
x
xf









f(x)
misal
u = sin 4x → u’ = 4 cos 4x
v = 2x → v’ = 2
x
x
2
4sin


18. y = [f(x)]n
y’ = n . [f(x)]n-1 . f’(x)
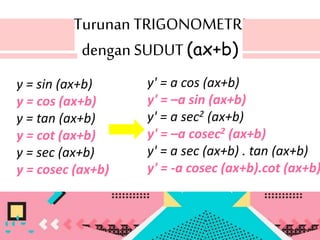
Turunan TRIGONOMETRI
BERPANGKAT

19. Turunan TRIGONOMETRI
BERPANGKAT
y = [f(x)]n
y’ = n . [f(x)]n-1 . f’(x)
Contoh
Tentukan turunan dari :
y = cos3 2x !
Jawab :
y = cos3 2x
y’ = 3 . cos2 2x . [2 (-sin 2x)]
y’ = 3 . cos2 2x . -2 sin 2x
y’ = -6 cos2 2x . sin 2x
y = cos (ax+b)
y’ = - a sin (ax+b)

20. Turunan TRIGONOMETRI
BERPANGKAT
y = [f(x)]n
y = n . [f(x)]n-1 . f’(x)
Contoh
Tentukan turunan dari :
y = sin4 3x + (2x - 5)4 !
Jawab :
y = sin4 3x + (2x - 5)4
y’ = 4 . sin3 3x (3 . cos 3x) + 4 (2x-5)3 (2)
y’ = 12 sin3 3x . Cos 3x + 8 (2x-5)3
y = sin (ax+b)
y’ = a cos (ax+b)

21. LATIHAN
1. Tentukan turunan dari :
a. f(x) = 2 (-cos x)
b. f(x) = 8 sin x
c. f(x) = 21 tan x
2. Tentukan turunan dari :
a. f(x) = 4 -sin x + 7 -cos x
b. f(x) = 3 sin x – cos x
3. Tentukan turunan dari
f(x) = cotan x
4. Tentukan turunan dari
5. Tentukan y’ dari
y = 3 sin2 x . Cos 2 x






 5
4
1
cos20)( xxf

22. Penyelesaian
1. Tentukan turunan dari :
a. f(x) = 2 -cos x
b. f(x) = 8 sin x
c. f(x) = 21 tan x
Jawab :
a. f(x) = 2 -cos x
f’(x) = 2 - (– sin x)
= 2 sin x
b. f(x) = 8 sin x
f’(x) = 8 cos x
c. f(x) = 21 tan x
f’(x) = 21 sec2 x

23. 2. Tentukan turunan dari :
a.f(x) = 4 -sin x + 7 -cos x
b.f(x) = 3 sin x – cos x
Jawab :
a. f(x) = 4 -sin x + 7 -cos x
f’(x) = 4 -cos x + 7 -(-sin x)
= - 4 cos x + 7 sin x
b. f(x) = 3 sin x – cos x
f’(x) = 3 cos x – (-sin x)
= 3 cos x + sin x
Penyelesaian

24. Tentukan turunan dari :
f(x) = cotan x
Jawab :
3 misal
u = cos x → u’ = - sin x
v = sin x → v’ = cos x
f(x) = sin x . cos x
f’(x) = u’ .v - u. v’
v2
= (- sin x) (sin x) - cos x.cos x
sin2 x
= – sin2x - cos2x
sin2 x
x
x
xf
xanxf
sin
cos
)(
cot)(


Penyelesaian

25. 3
Penyelesaian
misal
u = cos x → u’ = - sin x
v = sin x → v’ = cos x
f(x) = sin x . cos x
f’(x) = u’ .v - u. v’
v2
= (- sin x) (sin x) - cos x.cos x
sin2 x
= – sin2x - cos2x
sin2 x
= – 1 (sin2x + cos2x)
sin2 x
= -1 . 1
sin x . Sin x
= - cosec x . Cosec x
= - cosec2x

26. Tentukan turunan dari :





















5
4
1
sin5)(
5
4
1
sin.
4
1
.20)(
5
4
1
cos20)(
xxf
xxf
xxf






 5
4
1
cos20)( xxf
Penyelesai
an
4

27. Tentukan turunan dari :
y = sin3 x . Cos 2 x
misal
u = 3 sin2 x → u’ =6 sin x . cos x
v = Cos 2 x → v’ = -2 sin 2x
f(x) = sin x . cos x
f’(x) = u’ .v + u. v’
= (6 sin x .cos x) (Cos 2 x) + 3 sin2 x. -2 sin 2x
= 6 sin x cos x . Cos 2x – 6 sin2x . Sin 2x
Penyelesaian 5

28. Terima
Kasih