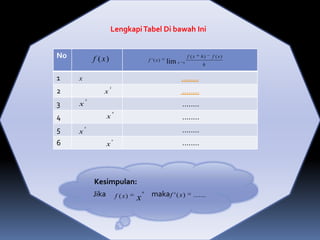
Dokumen ini membahas konsep limit fungsi dan turunan dalam pendidikan matematika, dengan tujuan untuk menentukan dan menyelesaikan masalah yang berkaitan dengan turunan fungsi. Berbagai rumus dan contoh disediakan untuk memfasilitasi pemahaman tentang perhitungan turunan. Kesimpulan menekankan pentingnya pemahaman tentang laju perubahan nilai fungsi dan aplikasinya dalam kalkulus.

1. Multimedia Pembelajaran Pendidikan Matematika
Desi Maulidyawati
0900095
Jurusan Pendidikan Matematika
Fakultas Pendidikan Matematika dan Ilmu Pengetahuan Alam
Universitas Pendidikan Indonesia
2012

2. Standar Kompetensi :
Menggunakan konsep limit
fungsi dan turunan fungsi
dalam pemecahan masalah
Kompetensi Dasar :
Menggunakan konsep dan aturan
turunan dalam perhitungan turunan
fungsi

3. Tujuan :
1. Dapat menentukan turunan fungsi.
2. Menyelesaikan masalah yang
berkaitan dengan turunan fungsi
sederhana.

4. Konsep, Sifat, dan
1. Menggunakan konsep dan aturan
Aturan dalam
turunan dalam perhitungan
Perhitungan Turunan
turunan fungsi
Fungsi

5. Perhatikan gambar grafik y = f(x) dengan domain pada
interval a x a h
berikut :
y
y = f( x)
f( . . . ) Q ( ... , ... )
f( . . . ) – f(a)
f(a)
P(... , ...)
h
x
o x=a x = ( . . . + . . .)
Perhatikan perubahan nilai x pada gambar di atas:

6. Jika x = a , maka kedudukan titik x berubah menjadi ......
y
a) a
y = f( x)
b) a+ h f( . . . ) Q ( ... , ... )
c) a - h f( . . . ) – f(a)
f(a)
P(... , ...)
h
x
o x=a x = ( . . . + . . .)
x mengalami perubahan sebesar:
(a+h) - a = h = h

7. Jawaban yang Anda berikan kurang tepat

8. Congratulation

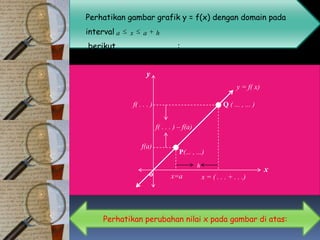
9. Maka y = f ( a ) juga berubah dari f ( a ) menjadi
…….
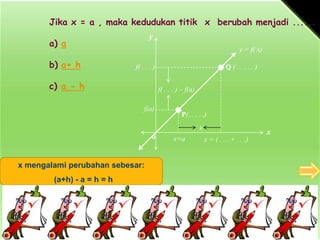
a) y = f(a+h) y
b) y = f(a-b) y = f( x)
f( . . . ) Q ( ... , ... )
c) y = f(a)
f( . . . ) – f(a)
f(a)
P(... , ...)
h
x
o x=a x = ( . . . + . . .)
nilai fungsi f mengalami perubahan sebesar:
[f(a+h) - f(a)]

10. Nilai rata-rata perbandingan perubahan nilai f ( x )
f ( x) .....
terhadap perubahan nilai x adalah :
x .....
a) f (x h) f (x)
h
b) f (x h) f ( x)
h
c) f (h x) f ( x)
x

11. y
y = f( x)
f( . . . ) Q ( ... , ... )
maka nilai h
f( . . . ) – f(a) akan semakin
kecil dan
f(a) mendekati nol
P(... , ...)
h
x
o x=a x = ( . . . + . . .)
Nilai limit dinamakan laju perubahan nilai fungsi f pada x
= a atau disebutmempunyai limit, atau turunan fungsi f(x)
akan juga differensial sehingga diperoleh:
pada x = a dan dinotasikan dengan f’(a).
f (... ...) f (...)
f '(x) lim h 0
....

12. Lengkapi Tabel Di bawah Ini
No f ( x) f '(x)
f (x h) f ( x)
lim h 0
h
1 x ........
2
2 x ........
3
3 x ........
4
4 x ........
5 x
5
........
n
6 x ........
Kesimpulan:
Jika f ( x) x
n
maka f ' ( x ) .......

13. f ( x) x
f (x h) x h
(x h) x
Maka: f '( x) lim h 0
h
h (x x)
lim h 0
h
1

14. 2
f (x) x
2
f (x h) ( x h)
2 2
Maka: f '( x) lim h 0
(x h) x
h
2 2 2
x 2 xh h x
lim h 0
h
2 2 2
lim (x x ) 2 xh h
h 0
h
2
2 xh h
lim h 0
h
h(2 x h)
lim h 0
h
2x 0
2x

15. Lengkapi Tabel Di bawah Ini
No f ( x) f (x h) f ( x)
f '(x) lim h 0
h
1 2x ......
2 2x
2 ......
3
3 2x ......
4
4 2x ......
5
5 2x ......
n
6 2x ......
Kesimpulan:
n
Jika f ( x) f maka f ' ( x) ......

16. f ( x) 2x
f (x h) 2( x h) 2x 2h
Maka: f ' ( x ) (2 x 2h) 2x
lim h 0
h
2h (2 x 2 x)
lim h 0
h
2h
lim h 0
h
2

17. 2
f ( x) 2x
2 2 2 2 2
f (x h) 2( x h) 2( x 2 xh h ) 2x 4 xh 2h
Maka:
2 2 2
(2 x 4 xh 2h ) 2 x
f '( x) lim h 0
h
2 2 2
(2 x 2 x ) ( 4 xh h )
lim h 0
h
h (4 x h)
lim h 0
h
lim h 0 4x h
4x 0
4x

19. Penyelesaian
a) x 3 4 x ....
3 1 1 -1
(3 x ) ( 4 x )
2
3x 4
4 3
b) 5x 3x 8 ....
4 1 3 1 (0 -1)
(5 4 ) x (3 3) x (8 0 ) x
3 2
20 x 8x

20. TERIMA KASIH
Sampai Jumpa