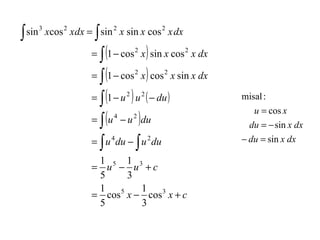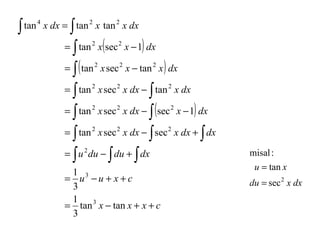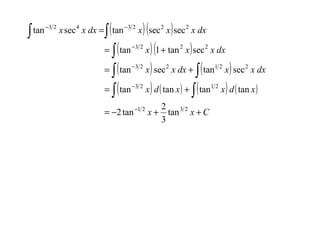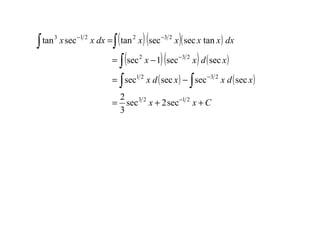Dokumen ini membincangkan integrasi trigonometri, khususnya cara mengintegrasi fungsi seperti ∫ sin n x dx dan ∫ cos n x dx berdasarkan sama ada n adalah ganjil atau genap. Ia menerangkan penggunaan identiti trigonometri untuk menyederhanakan fungsi dan memberikan pelbagai contoh pengiraan. Terdapat juga perbincangan mengenai bentuk yang melibatkan tan dan cot dalam integrasi.

1. INTEGRAL TRIGONOMETRI

2. Bentuk
∫
sin n x dx dan
∫
cos n x dx
• Jika n adalah bilangan bulat positif ganjil, maka:
sin n x = sin x sin n −1 x dan cos n x = cos x cos n −1 x
dan gunakan sin 2 x + cos2 x = 1
• Jika n adalah bilangan bulat positif genap, maka:
1 − cos 2 x
sin x =
2
2
1 + cos 2 x
cos x =
2
2

3. 1.
∫
2
 1 + cos 2 x 
cos x dx = 
 dx
2


4
∫
 1 + 2 cos 2 x + cos 2 2 x 
 dx
= 


4


1
=
1 + 2 cos 2 x + cos 2 2 x dx
4
1
=
dx + 2 cos 2 x dx + cos 2 2 x dx
4
1
 1 + cos 4 x  
=  dx + 2 cos 2 xdx + 
 dx 


4
2

 
∫
∫(
(∫
∫
)
∫
)
∫
∫
∫
1
1

=  dx + 2 cos 2 xdx + (1 + cos 4 x ) dx 
4
2

∫
∫
∫
(∫
)
1
1

=  dx + 2 cos 2 xdx +
dx + cos 4 xdx 
4
2

3
1
1
= x + sin 2 x + sin 4 x + c
8
4
32
∫
∫
∫

4. ∫
∫
= ∫ (1 − cos x ) sin x dx
= ∫ (1 − u ) ( − du )
= ∫ (u − 1) du
= ∫ u du − ∫ du
sin 3 x dx = sin 2 x sin x dx
2
2
2
2
1 2+1
=
u −u +c
2 +1
1
= u3 − u + c
3
1
3
= ( cos x ) − cos x + c
3
1
= cos 3 x − cos x + c
3
misal :
u = cos x
du = − sin x dx
− du = sin x dx

5. ∫
sin 4 x dx =
∫ (sin x ) dx
2
2
2
 1 − cos 2 x 
= 
 dx
2


 1 − 2 cos 2 x + cos 2 2 x 
dx
= 


4


1
=
1 − 2 cos 2 x + cos 2 2 x dx
4
1
=
dx − 2 cos 2 x dx + cos 2 2 x dx
4
1
 1 + cos 4 x  
=  dx − 2 cos 2 x dx + 
 dx 


4
2

 
∫
∫
∫(
(∫
∫
)
∫
)
∫
∫
∫
1
1
(1 + cos 4 x ) dx 
=  dx − 2 cos 2 x dx +

4
2

1
1
1

=  dx − 2 cos 2 x dx +
dx +
cos 4 x dx 
4
2
2

3
1
1
= x − sin 2 x + sin 4 x + c
8
4
32
∫
∫
∫
∫
∫
∫
∫

6. ∫
Bentuk
sin m x cos n x dx
• Untuk n atau m ganjil, keluarkan sin x atau cos x
kemudian gunakan identitas:
sin 2 x + cos2 x = 1
• Untuk n dan m genap, tuliskan sinmx dan cosnx menjadi
jumlah suku-suku dalam cosinus, gunakan identitas:
1 − cos 2 x
sin x =
2
1 + cos 2 x
cos x =
2
2
2
cos2 x = 2cos 2 x − 1
atau
cos 2 x = 1 − 2sin 2 x

7. ∫
∫
sin 3 xcos 2 xdx = sin 2 x sin x cos 2 x dx
)
∫(
= ∫ (1 − cos x ) cos x sin x dx
= ∫ (1 − u ) u ( − du )
= ∫ (u − u ) du
= ∫ u du − ∫ u du
= 1 − cos 2 x sin x cos 2 x dx
2
2
4
4
2
2
2
2
1
1
= u5 − u3 + c
5
3
1
1
5
= cos x − cos 3 x + c
5
3
misal :
u = cos x
du = − sin x dx
− du = sin x dx

8. ∫
2
 1 − cos 2 x  1 + cos 2 x 
sin 2 x cos 4 xdx = 

 dx
2
2



1
(1 − cos 2 x ) 1 + 2 cos 2 x + cos 2 2 x dx
=
8
1
=
1 + cos 2 x − cos 2 2 x − cos 3 2 x dx
8
1 
1

2
=
1 + cos 2 x − (1 + cos 4 x ) − cos 2 x cos 2 x  dx
8 
2

∫
(
∫
)
∫(
)
∫
(
)
1 
1

1 + cos 2 x − (1 + cos 4 x ) − 1 − sin 2 2 x cos 2 x  dx

8 
2

1 1 1

2
=
 − cos 4 x + sin 2 x cos 2 x  dx
8 2 2

=
∫
∫
1 1
1

= 
dx −
cos 4 x dx + sin 2 2 x cos 2 x dx 
8 2
8

11
1
1

=  x − ⋅ 4 sin 4 x + sin 2 2 x  + C
8 2
8
6

∫
∫
∫
misal :
u = sin 2 x
du = 2 cos 2 x dx
1
du = cos 2 x dx
2

9. Bentuk
∫ tan
n
x dx dan
• Gunakan identitas
tan 2 x = sec 2 x −1
cot 2 x = csc 2 x − 1
∫ cot
n
x dx

10. ∫
∫
= ∫ tan x (sec x − 1) dx
= ∫ ( tan x sec x − tan x ) dx
= ∫ tan x sec x dx − ∫ tan x dx
= ∫ tan x sec x dx − ∫ (sec x − 1) dx
= ∫ tan x sec x dx − ∫ sec x dx + ∫ dx
= ∫ u du − ∫ du + ∫ dx
tan 4 x dx = tan 2 x tan 2 x dx
2
2
2
2
2
2
2
2
2
2
2
2
1 3
= u −u + x +c
3
1
= tan 3 x − tan x + x + c
3
2
2
2
misal :
u = tan x
du = sec 2 x dx

11. Bentuk
∫
tan m x sec n x dx
dan
∫
cot m x csc n x dx
• Jika n genap dan m sembarang, maka keluarkan faktor
sec2x atau cosec2x
• jika n sembarang dan m ganjil, maka keluarkan faktor
tan x . sec x

12. ∫
∫(
)(
)
tan −3 2 x sec 4 x dx = tan −3 2 x sec 2 x sec 2 x dx
∫ ( tan
= ∫ ( tan
= ∫ ( tan
=
−3 2
−3 2
−3 2
)(
)
x ) sec x dx + ∫ ( tan x ) sec x dx
x ) d ( tan x ) + ∫ ( tan x ) d ( tan x )
x 1 + tan 2 x sec 2 x dx
= −2 tan −1 2 x +
2
12
12
2
tan 3 2 x + C
3
2

13. ∫
)(
)
∫(
= ∫ (sec x − 1) (sec
x ) d ( sec x )
= ∫ sec x d ( sec x ) − ∫ sec
x d ( sec x )
tan 3 x sec −1 2 x dx = tan 2 x sec −3 2 x ( sec x tan x ) dx
2
12
−3 2
−3 2
2
= sec 3 2 x + 2 sec −1 2 x + C
3