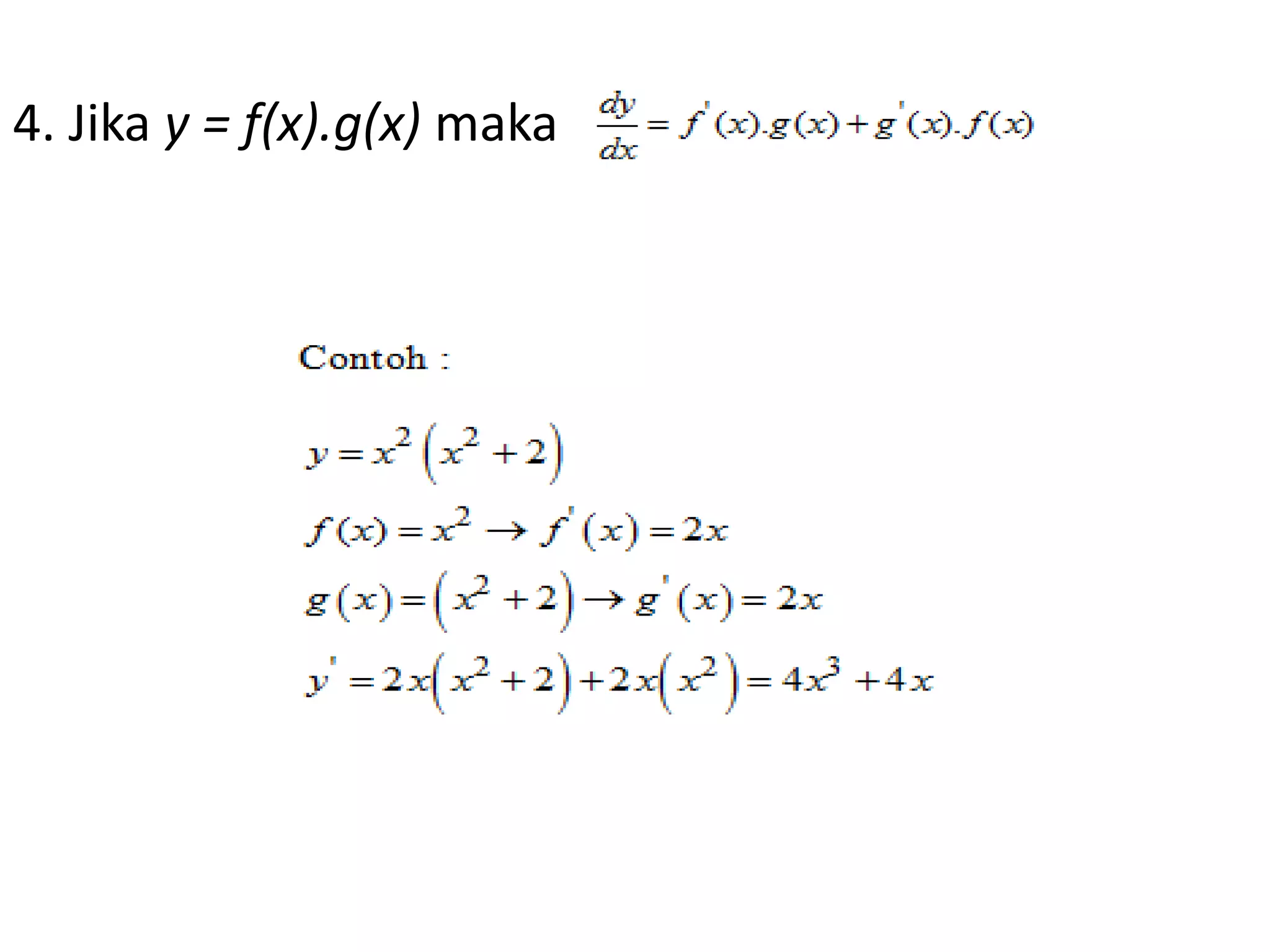Embed presentation
Downloaded 30 times




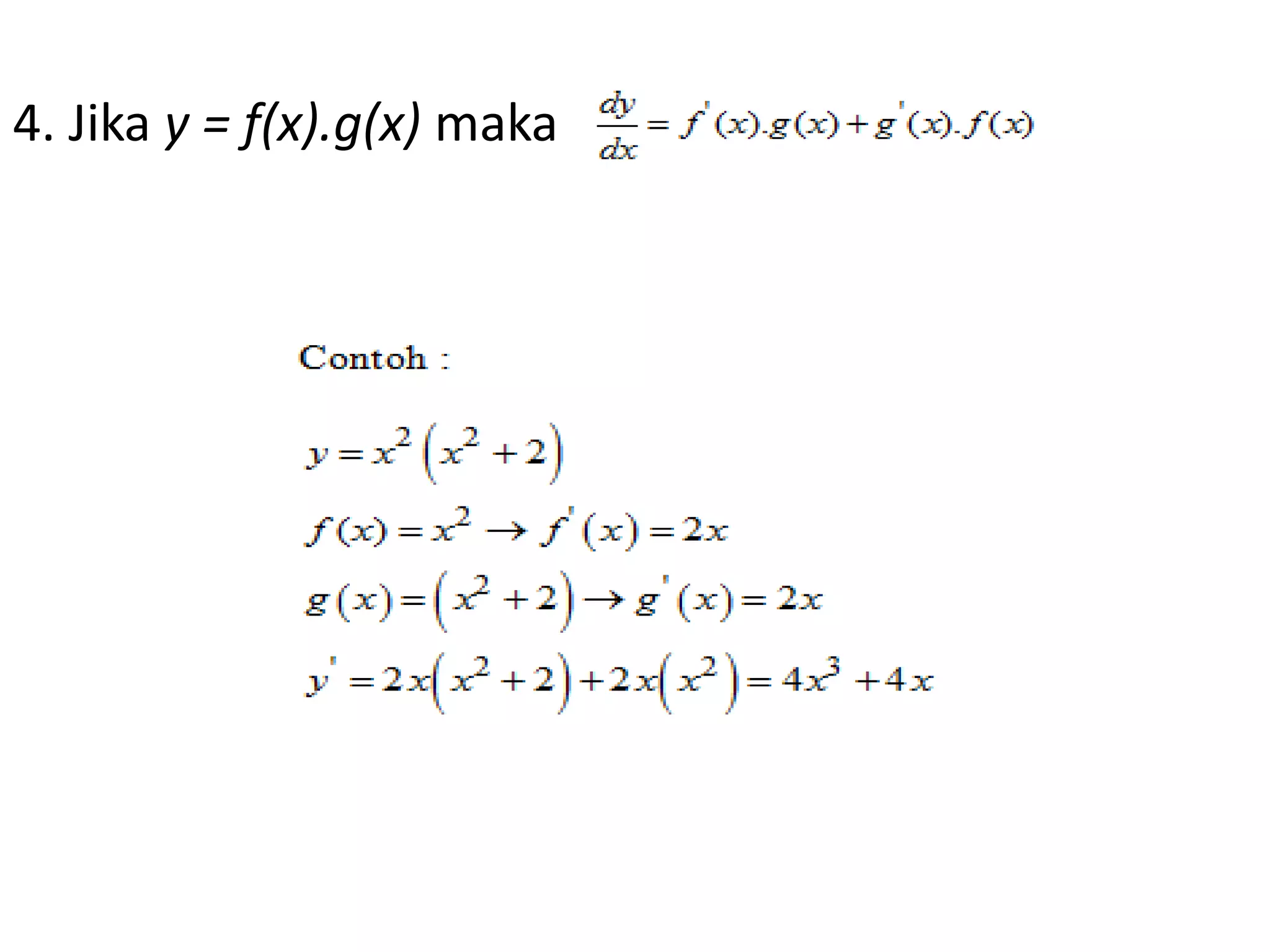


Dokumen ini memberikan definisi turunan dan beberapa rumus turunan yang sering digunakan. Turunan didefinisikan sebagai laju perubahan fungsi terhadap variabel bebasnya. Rumus-rumus turunan meliputi turunan fungsi konstan, turunan jumlah dan hasil kali fungsi, serta turunan fungsi kuadrat dan kubik.