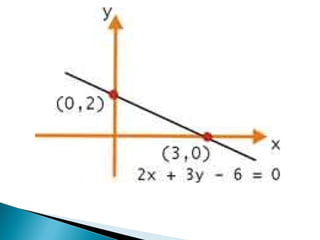
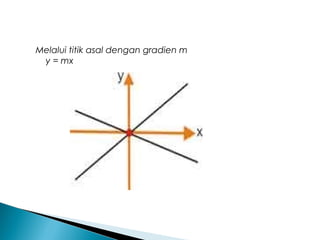
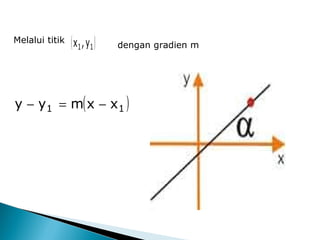
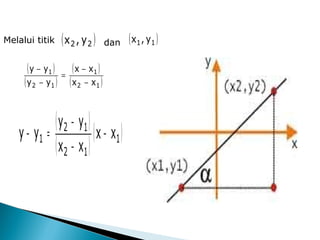
Dokumen tersebut membahas tentang diferensial dan penerapannya, termasuk definisi koefisien diferensial baku, teorema-teorema turunan, aturan-aturan diferensiasi, dan contoh soal penerapan diferensial untuk menentukan persamaan garis, garis singgung dan normal kurva, serta grafik persamaan.

1. DIFERENSIAL

2.  2.1. Koefiesien Diferensial baku.
 2.2 Fungsi dari suatu fungsi
 2.3 Diferensial Logaritmik
 2.4 Persamaan Parametrik

3. Teorema Turunan 1 :
Jika ada, maka f kontinu di c.

4. Teorema Turunan 2 :
1. Aturan Fungsi Konstanta. Jika = k dengan k suatu
konstanta maka untuk sebarang x, = 0, yaitu = 0.
2. Aturan fungsi Identitas. Jika = x, maka = 1, yaitu
=1.
3. Aturan Pangkat. Jika , dengan n bilangan-
bilangan bulat positif, maka , yaitu
.
4. Aturan Kelipatan Konstanta. Jika k suatu konstant dan f
suatu fungsi yang terdiferensialkan, maka ,
yaitu .

5. 5. Aturan Jumlah. Jika f dan g fungsi-fungsi yang
terdiferensialkan, maka , yaitu
.
6. Aturan Selisih. Jika f dan g fungsi-fungsi yang
terdiferensialkan, maka
, yaitu .
7. Aturan Hasil Kali. Misalkan f dan g fungsi-fungsi yang
dapat terdiferensialkan, maka ,
yaitu .
8. Aturan Hasil Bagi. Misalkan f dan g fungsi-fungsi yang
dapat didiferensialkan dengan . Maka
,yaitu : .

6. Misalkan , fungsi
1. .
2. .
3. .

7. 1.
2.
3.
4.
5.
6.

8. Misalkan adalah fungsi
yang dapat diturunkan. Maka :
1.
2.
3.
4.
5.
6.

9. Misalkan , fungsi
1. .
2. .
3. .

10. Misalkan dan menentukan
fungsi komposit .
Jika g terdiferensialkan di x
dan f terdiferensialkan di ,
maka terdiferensialkan di x
dan ,
yaitu .

11. Contoh :
1.Diferensialkan y = Cos ( 5x – 4 )
Jawab :
dy/dx = - 5 sin ( 5x – 4 )
2. Diferensialkan y = tan ( 4 – 5x )
jawab:
dy / dx = -5 sec ( 4 – 5x )

12. Untuk fungsi implisit yang sukar dinyatakan
secara eksplisit, turunannya dapat ditentukan
dengan menggunakan aturan turunan untuk
jumlah dan perkalian dua fungsi dan aturan berantai.

13. Contoh :
Pandang persamaan :

14. Pandang fungsi-fungsi: dan
Maka :
atau

15.  Purnami.E.Soewardi,Media Pembelajaran
Matematika,Bandung ,2008
 K.Astroud, Erwin Sucipto, Matematika Untuk
Teknik, PT. Gelora Aksara Pratama,1987.

16. PENERAPAN DIFERENSIAL

17. Persamaan Garis lurus dan garis normal
a) Persamaan garis lurus adalah y = mx + c
Dengan m : kemiringan garis / gradien
Atau m = dy/dx = tan θ
Sedangkan c : perpotongan dengan sumbu y
b) y – y1 = m ( x – x1)

18. Contoh soal :
1. Tentukan persamaan garis yang
melalui titik P (3,2 ) dan Q ( -2,1 )
penyelesaian :
y = mx + c
Melalui P ( 3,2 ) …… 2 = 3m + c
Melalui Q ( -2,1 ) …… 1 = -2m + c
 -
1 = 5m
m = 1/5
maka c = 7/5
Jadi persamaan garisnya adalah y = 1/5 x + 7/5

19. Contoh Soal:
2.Tentukan persamaan garis singgung & garis
normal kurva
x + y + 3xy – 11 = 0 di titik ( 1,2 )
Jawab :
Diferensialkan persamaan kurvanya
2x +2y. dy/dx + 3y + 3x. dy/dx = 0
dy/dx ( 2y + 3x ) = -2x – 3y
dy/dx = - 8/7
m = - 8/7

20. Jadi persamaan garis singgungnya adalah
y - y = m ( x - x )
y –2 = - 8/7 ( x – 1 )
y = - 8/7 x + 8/7 + 2
7y = -8x + 22
Kemiringan garis normalnya , m = 7/8
Persamaan garis normalnya adalah
Y –2 = 7/8 (x – 1 )
Y = 7/8 x – 7/8 +2
8y = 7x + 9

21. Kemiringan garis Normal =
ggunggariskemiringan sin
1−

22.
 Cukup dengan menentukan 2 buah titik sembarang
yang terletak pada grafik tersebut, kemudian
dihubungkan (biasanya kedua titik ini adalah titik-
titik potong dengan masing-masing sumbu).
 contoh:
 Gambarkan grafik 2x + 3y - 6 = 0
 Titik potong dengan sumbu x ® y = 0 ; 2x + 3(0) - 6
= 0 ® x = 3 ® (3,0)
 Titik potong dengan sumby y ® x = 0 ; 2(0) + 3y - 6
= 0

24.  1.Bentuk umum
ax + by + c = 0 atau y = mx + n
 2. Persamaan sumbu x ® y = 0
 3. Persamaan sumbu y ® x = 0
 4. Sejajar sumbu x ® y = k
 5. Sejajar sumbu y ® x = k

25. Melalui titik asal dengan gradien m
y = mx

26. ( )11 y,x
( )11 xxmyy −=−
Melalui titik
dengan gradien m

27. ( )11 y,x( )22 y,x
( )
( )
( )
( )12
1
12
1
xx
xx
yy
yy
−
−
=
−
−
( )
( )
( )1
12
12
1 xx
xx
yy
yy −
−
−
=−
Melalui titik dan

28. Y Tali busur
B
Garis singgung
A h
0 c c+h X

29. Misalkan kurva tersebut mempunyai persamaan .
Maka titik A mempunyai koordinat ,
titik B mempunyai koordinat
dan tali busur yang melewati A dan B mempunyai
kemiringan (gradien) , dengan
Akibatnya, garis singgungnya adalah
garis yang melalui A dengan gradien :
.

30.  Purnami.E.Soewardi,Media Pembelajaran
Matematika,Bandung ,2008