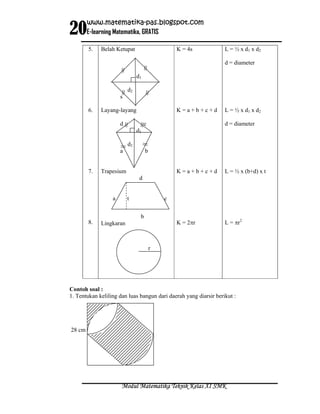
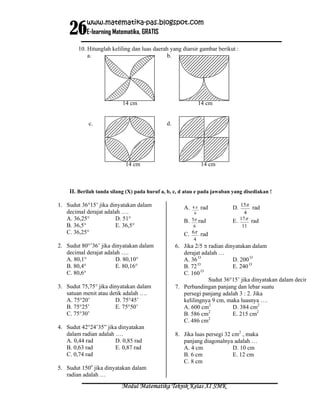
Dokumen ini membahas tentang sudut, termasuk pengertian, pengukuran, dan satuan seperti derajat dan radian. Terdapat contoh soal yang berkaitan dengan konversi satuan sudut dan perhitungan keliling serta luas bangun datar. Selain itu, dokumen ini juga memberikan latihan dan evaluasi mengenai materi yang dibahas.

1. 17
www.matematika-pas.blogspot.com
E-learning Matematika, GRATIS
Penyusun
: Tri Wahyu Suciati, S.Pd. ; Hilyatun Nadzifah, S.Pd. ;
Bambang Wahyudi, S.Pd. ; Endah Setya Prihati, S.Pd.
Editor : Drs. Keto Susanto, M.Si. M.T. ; Istijab, S.H. M.Hum.
Imam Indra Gunawan, S.Si.
A. MENGIDENTIFIKASI SUDUT
1. Pengertian sudut
Sudut adalah suatu daerah yang dibentuk oleh dua sinar garis yang titik
pangkalnya bertemu.
C
AB dan AC adalah sinar garis dan A adalah titik sudut. α
adalah besar sudut yang dibentuk sinar garis AB dan AC
α
A B
2. Mengukur besar suatu sudut
Pengukuran besar suatu sudut diperlukan satuan untuk mengukurnya. Satuan
ukuran sudut yang digunakan adalah derajat dan radian.
a. Satuan derajat ( ° )
1
Satu putaran penuh besarnya 360° sehingga 1° besarnya putaran.
360
Satuan ukuran yang lebih kecil adalah menit (’ ) dan detik ( ’’), dengan
1° adalah 60 menit dan 1 menit = 60 detik sehingga :
° °
⎛ 1 ⎞ ⎛ 1 ⎞
1' = ⎜ ⎟ dan 1' ' = ⎜ ⎟
⎝ 60 ⎠ ⎝ 3600 ⎠
Contoh soal :
1) Nyatakan ukuran sudut berikut hanya dalam satuan derajat
a) 45°30’
b) 50°15’25”
Jawab :
a) 45°30’ = 45° + 30’ b) 50°15’25” = 50° + 15’ + 25”
30 15 25
= 45° + ( )° = 50° + ( )° + )°
60 60 3600
= 45° + 0,5° = 50° + 0,25° +
0,0069°
= 45,5° = 50,2569°
2) Nyatakan ukuran sudut berikut dalam ukuran derajat, menit dan detik
a) 36,26°
b) 43,84°
Jawab :
a) 36,26° = 36° + 0,26° b) 43,84° = 43° + 0,84°
= 36° + (0,26 x 3600)” = 43° + (0,84 x 3600)”
= 36° + 936” = 43° + 3024”
= 36°15’36” = 43°50’24”
MGMP Matematika SMK kota Pasuruan

2. 18
www.matematika-pas.blogspot.com
E-learning Matematika, GRATIS
b. Satuan radian (rad)
Satuan radian adalah besarnya sudut pusat suatu lingkaran yang menghadap
busur lingkaran, yang panjangnya sama dengan panjang jari-jari lingkaran.
1 radian Misal : 1 radian = x
x r
=
r 360 2πr
α x 1
=
r 360 2π
2πx = 360
180
x =
π
Jadi :
°
⎛ 180 ⎞ ⎛ π ⎞
1radian = ⎜ ⎟ 1° = ⎜ ⎟radian
⎝ π ⎠ ⎝ 180 ⎠
Contoh soal :
1. Ubah ukuran sudut ke satuan radian
a. 30°
b. 250°
Jawab :
π π
a. 30° = 30 x radian b. 250° = 250 x radian
180 180
1
π radian
= = 4,36 radian
6
2. Ubah ukuran sudut ke satuan derajat
a. 4 radian
2
b. π radian
3
Jawab :
180
a. 4 radian = 4 x ( )° = 229,94°
π
2 2 180
b. π radian = π x ( )° = 120°
3 3 π
Latihan 1 :
1. Hitunglah :
a. 58021′ + 47049′43” d. 32034’ - 27047’
b. 36025′41” + 52042′22” e. 41052′38” - 19042′59”
c. 45055′34” + 28042′43” f. 56017′38” + 24038′43”
2. Nyatakan dengan satuan derajat (0) dari soal-soal berikut ini!
a. 300 45′ b. 920 30′ c. 270 36′45” d. 210 27′24”
Modul Matematika Teknik Kelas XI SMK

3. 19
www.matematika-pas.blogspot.com
E-learning Matematika, GRATIS
3. Ubahlah ukuran-ukuran sudut berikut ke dalam satuan derajat, menit, dan detik!
a. 23,50 b. 30,060 c. 47,210 d. 65,750
4. Ubahlah satuan sudut dibawah ini ke dalam satuan radian !
a. 300 b. 1200 c. 4800 d. 7500
5. Nyatakan sudut-sudut di bawah ini dalam satuan derajat!
1 2 1
a. π radian b. π radian c. 2 π radian d. 2,5 radian
4 5 6
B. MENENTUKAN KELILING DAN LUAS DAERAH BANGUN DATAR
a. Menentukan Keliling dan Luas Daerah Bangun Datar yang Beraturan
No Bangun Datar Keliling Luas
1. Persegi K = 4s L=sxs
s
2. Persegi Panjang K = 2(p + l) L=pxl
l
p
3.
Segitiga
K=a+b+c L = ½ x alas x tinggi
L = S(S-a)(S-b)(S-c)
a t b
untuk S =½ (a+b+c)
L
c
4.
Jajar Genjang
K=a+b+c+d L = alas x tinggi
d
a t c
L
b
MGMP Matematika SMK kota Pasuruan

4. 20
www.matematika-pas.blogspot.com
E-learning Matematika, GRATIS
5. Belah Ketupat K = 4s L = ½ x d1 x d2
d = diameter
d1
d2
s
6. Layang-layang K=a+b+c+d L = ½ x d1 x d2
d c d = diameter
d1
d2
a b
7. Trapesium K=a+b+c+d L = ½ x (b+d) x t
d
a t c
b
8. Lingkaran K = 2πr L = πr2
r
Contoh soal :
1. Tentukan keliling dan luas bangun dari daerah yang diarsir berikut :
28 cm
Modul Matematika Teknik Kelas XI SMK

5. 21
www.matematika-pas.blogspot.com
E-learning Matematika, GRATIS
Jawab :
. K1 = keliling berupa garis lurus K2 = keliling berupa garis lengkung
3
= 7 + 7 + 2( 72 + 72) = keliling lingkaran
4
3 22
= 33,8 m = (2 x x 7) = 33 m
4 7
Total keliling = 33,8 + 33 = 66,8 m
L1 = mencari luas daerah yang bentuknya ada dua bagian
= 2 ( luas persegi – luas ¼ lingkaran )
1 22
= 2{(7x7)-( x x7x7)}
4 7
= 2(49 – 38,5)
= 21 m2
L2 = mencari luas daerah yang bentuknya ada satu bagian
= luas ¼ lingkaran
1 22
= x x7x7
4 7
= 38,5 m2
L2 = mencari luas daerah yang bentuknya ada dua bagian
= luas segitiga
= ½ x7x7
= 24,5 m2
Total luas = 21 + 38,5 +24,5
= 84 m2
2. Sebuah jendela berbentuk persegi panjang dengan panjang 120 cm lebar 70 cm dan
bagian atas ada fentilasi berbentuk setengah lingkaran yang panjang diameternya
sama dengan lebar jendela, tentukan keliling dan luas jendela tersebut.
Jawab :
22
Keliling jendela = 120 + 70 + 120 + (½ x x 70)
7
= 420 cm 70cm
22
Luas jendela = (120 x 70 ) + (½ x x 35 x 35 ) 120 cm
7
= 8400 + 1925
= 10325 cm2
b. Menentukan Luas Bangun Datar Tidak Beraturan
1) Aturan Trapesoida
L1 L2
L3
y1 y2 y3 y4
a
MGMP Matematika SMK kota Pasuruan

6. 22
www.matematika-pas.blogspot.com
E-learning Matematika, GRATIS
L1 = ½ x ( y 1 + y 2 ) x a L2 = ½ x ( y 2 + y 3 ) x a L3 = ½ x ( y 3 + y 4 ) x a
Total luas ≈ L1 + L2 + L3
≈ ½ ( y1 + y 2 ) a + ½ ( y2 + y3 ) a + ½ x ( y3 + y 4 ) a
≈ ½ a { ( y1 + y2 ) + ( y2 + y3 ) + ( y3 + y4 ) }
≈ ½ a ( y1 + 2 y2 + 2y3 + y4 )
≈ a { ½ (y1 + y4) + y2 + y3 }
Contoh soal :
Hitunglah luas daerah berikut !
2m 6m 7m 7m 7m 5m 3m
3m
L ≈ a { ½ (y1 + y7) + y2 + y3 + y4 + y5 + y6 }
≈ 3 { ½ (2 + 3) + 6 + 7 + 7 + 7 + 5 )
≈ 3 ( 2,5 + 32 )
≈3 x 34,5
≈ 103,5 m
1) Aturan Koordinat
L = (a + ½ b) x luas persegi
a = banyaknya persegi yang utuh
b = banyaknya persegi yang tidak utuh
Contoh soal :
Hitunglah luas daerah yang diarsir berikut !
Y
X
Jawab :
a = 33
b = 22
L ≈ ( 33 + ½ .22) x satu satuan luas
≈ 44 satuan luas
Modul Matematika Teknik Kelas XI SMK

7. 23
www.matematika-pas.blogspot.com
E-learning Matematika, GRATIS
Latihan 2 :
1. Hituglah keliling dan luas segitiga yang panjang sisinya 6cm, 7cm, dan 11cm!
2. Hitunglah keliling lingkaran yang luasnya 3.850 cm2 !
3. Tentukan keliling dan luas banguan dibawah ini !
10 cm D
a. c.
5 cm
8 cm A C
12 cm
16 cm B
b. D 20 cm C d. 5 cm
t 17 cm 4
cm
25 cm 450
A E B
4. Pada belah ketupat EFGH diketahui panjang sisi EF = (4x – 2) cm dan panjang
sisi GH = (2x + 4) cm. Tentukan panjang sisi-sisi belah ketupat !
5. Perbandingan panjang sisi-sisinyang sejajar suatu trapesium adlah 4 : 3. Jika
tingginya 8 cm da luasnya 84 cm2, tentukanlah panjang sisi yang sejajar !
6. Roda sebuah sepeda berputar sebanyak 900 kali untuk melintasi jalan sepanjang
847,8 m. Hitunglah :
a. keliling roda
b. panjang jarai-jari roda
7. Pak Wira akan membuat taman berbentuk lingkaran dengan jari-jari 42 m.
Dalam taman itu terdapat kolam yang permukaannya berukuran 18 m x 15 m.
Jika tiap 1 m2 taman memerlukan pupuk 50 gram, berapa kg pupuk yang
diperlukan untuk taman tersebut !
8. Hitunglah luas daerah yang diarsir berikut :
28 m
MGMP Matematika SMK kota Pasuruan

8. 24
www.matematika-pas.blogspot.com
E-learning Matematika, GRATIS
9. Hitunglah luas daerah pada gambar dibawah ini dengan metode mid ordinat!
10. Hitunglah luas daerah pada gambar dibawah ini dengan metode trapesium !
Latihan 3:
Lengkapi setiap jawaban soal berikut ini
1. Nyatakan sudut 52°26’ dalam radian
Jawab : 52°26’ = ……
π
= …… x radian
....
= ……. π radian
2. Nyatakan sudut 2/3 π radian dalam derajat
2 2 ......°
Jawab : π radian = π x
3 3 π
= ……°
3. Pada layang-layang PQRS, diketahui panjang PQ = 15 cm, QR = 20 cm . Diagonal
PR dan QS berpotongan di T dengan TQ =TS = 12 cm. Tentukan layang-layang
PQRS !
Jawab :
PT2 = 152 - …. TR2 = 202 - …. Luas PQRS = ½ x QR x …..
= 225 - …. = 400 - …. = ½ x (QT+TS) x
(PT+TR) = …. = …. = ½ x (12+12) x ( … + ….)
PT = ….. TR = …. = ½ x 24 x …. = …..cm 2
Modul Matematika Teknik Kelas XI SMK

9. 25
www.matematika-pas.blogspot.com
E-learning Matematika, GRATIS
4. Tentukan luas dan keliling bangun berikut
10 m Jawab :
t 2 = 132 - … K = 15 + 13 + 10 + …..
= 169 - … = ……… m
t 13 m = ……
t = …. L = ½ x (10 + ….) x ….
= ½ x ……. x ……
= ………m2
15 m
== oOo ==
EVALUASI
I. Jawablah soal berikut dengan singkat dan jelas !
1. Ubah satuan sudut dibawah ini ke derajat decimal !
a. 46°45’ c. 76°130”
b. 60°20’80” d. 46°40’65”
2. Ubah satuan sudut di bawah ini ke menit atau detik !
a. 30,43° c. 50,50°
b. 5,555° d. 32,23°
3. Ubah satuan sudut di bawah ini ke radian !
a. 50° c. 335°
b. 120° d. 750°
4. Ubah satuan sudut berikut ke derajat !
a. ½ radian c. 2,6 radian
b. 4 π radian d. 5,5 radian
5
5. PQRS adalah layang-layang dengan panjang PQ sebesar 20 cm, PR sebesar 21
cm. Jika luas PQRS = 352 cm2, hitunglah panjang QR !
6. Suatu persegi panjang, panjangnya (4x + 1) cm, lebarnya 8 cm. Jika luasnya 104
cm2 tentukan kelilingnya !
7. Amir akan membuat taman berbentuk lingkaran dengan diameter 500 dm.
Disepanjang taman dibuat jalan yang lebarnya 2 m mengelilingi taman. Jika
biaya pembuatan jalan Rp. 120.000,00 setiap m2. Hiutunglah biaya pembuatan
jalan tersebut !
8. Panjang jarum menitan sebuah jarum jam adalah 15 cm. Hitunglah panjang
lintasan jarum tersebut selama berputar 20 menit !
9. Luas daerah belah ketupat sama dengan 54 cm2. Jika perbandingan diagonalnya
3 : 1, tentukan panjang sisi belah ketupat tersebut !
MGMP Matematika SMK kota Pasuruan

10. 26
www.matematika-pas.blogspot.com
E-learning Matematika, GRATIS
10. Hitunglah keliling dan luas daerah yang diarsir gambar berikut :
a. b.
14 cm 14 cm
c. d.
14 cm 14 cm
II. Berilah tanda silang (X) pada huruf a, b, c, d atau e pada jawaban yang disediakan !
1. Sudut 36°15’ jika dinyatakan dalam A. 4π rad D. 15π rad
decimal derajat adalah …. 6 4
A. 36,25° D. 51° B. 5π rad E. 17π rad
B. 36,5° E. 36,5° 6 11
C. 36,25° C. 6π rad
4
2. Sudut 80°’36’ jika dinyatakan dalam 6. Jika 2/5 π radian dinyatakan dalam
decimal derajat adalah …. derajat adalah …
A. 80,1° D. 80,10° A. 36 O D. 200 O
O
B. 80,4° E. 80,16° B. 72 E. 240 O
C. 80,6° C. 160 O
Sudut 36°15’ jika dinyatakan dalam decim
3. Sudut 75,75° jika dinyatakan dalam 7. Perbandingan panjang dan lebar suatu
satuan menit atau detik adalah …. persegi panjang adalah 3 : 2. Jika
A. 75°20’ D. 75°45’ kelilingnya 9 cm, maka luasnya ….
B. 75°25’ E. 75°50’ A. 600 cm2 D. 384 cm2
2
C. 75°30’ B. 586 cm E. 215 cm2
2
C. 486 cm
4. Sudut 42°24’35” jika dinyatakan
dalam radian adalah …. 8. Jika luas persegi 32 cm2 , maka
A. 0,44 rad D. 0,85 rad panjang diagonalnya adalah …
B. 0,63 rad E. 0,87 rad A. 4 cm D. 10 cm
C. 0,74 rad B. 6 cm E. 12 cm
C. 8 cm
5. Sudut 150o jika dinyatakan dalam
radian adalah …
Modul Matematika Teknik Kelas XI SMK

11. 27
www.matematika-pas.blogspot.com
E-learning Matematika, GRATIS
9. Selembar kertas berbentuk persegi 15. Persegi panjang, panjangnya sama
panjang berukuran 20 cm x 15 cm. dengan 2 kali lebarnya. Jika
Jika keempat pojok kertas tersebut panjangnya dikurangi 5 cm dan
dipotong berbentuk persegi dengan lebarnya ditambah 1 cm, sama
sisi 2,5 cm, maka keliling kertas bentuknya menjadi persegi. Luas
setelah dipotong adalah … daerah persegi tersebut adalah ….
A. 60 cm D. 90 cm A. 16 cm2 D. 49 cm2
2
B. 70 cm E. 100 cm B. 25 cm E. 33 cm2
2
C. 80 cm C. 36 cm
10. OABC adalah jajar genjang. Jika O 16. Luas belah ketupat adalah 216 cm2
titik pangkal koordinat A(4,7) dan dan panjang salah satu diagonalnya
B(8,6) maka koordinat titik C adalah adalah 24 cm. Keliling belah ketupat
…. tersebut adalah …
A. (1,4) D. (2,4) A. 60 cm D. 30 cm
B. (1,5) E. (2,5) B. 48 cm E. 28 cm
C. (4,1) C. 42 cm
11. Luas belah ketupat yang panjang 17. Perbandingan diagonal suatu belah
diagonal-diagonalnya 5 cm dan 12 cm ketupat adalah 3 : 4. Bila keliling
adalah …. belah ketupat tersebut 40 cm maka
A. 7 cm2 D. 30 cm2 luasnya adalah …..
2
B. 9 cm E. 60 cm2 A. 24 cm2 D. 100 cm2
2 2
C. 17cm B. 48 cm E. 112 cm2
2
C. 96 cm
12. Luas layang-layang adalah 72 cm2.
Jika salah satu diagonalnya 9 cm, 18. Jari-jari sebuah lingkaran yang
maka panjang diagonal yang lain luasnya 3.850 m adalah …..
adalah … A. 20 m D. 35 m
A. 7 cm D. 12 cm B. 25 m E. 40 m
B. 8 cm E. 16 cm C. 30 m
C. 9 cm
19. Keliling daerah yang berbentuk
13. Suatu trapezium panjang sisi-sisi setengah lingkaran dengan jari jari 7
yang sejajar adalah 9 cm dan 4 cm. cm adalah …
Jika luas trapezium tersebut 39 cm2, A. 22 cm D. 26 cm
maka tingginya adalah … B. 29 cm E. 51 cm
A. 1,5 cm D. 5 cm C. 44 cm
B. 3 cm E. 6 cm
C. 4 cm 20. Luas bangun tak beraturan di bawah
ini adalah …
14. Sebuah persegi panjang (3x – 2)cm
dan lebarnya (x + 3) cm. Jika A. 48 m
kelilingnya 42 cm, maka panjangnya B. 50 m
aadlah …. 10 8 8 10 12 C. 54 m
A. 5 cm D. 14 cm D. 60 m
B. 8 cm E. 15 cm 2m E. 75 m
C. 12 cm
MGMP Matematika SMK kota Pasuruan

12. 28
www.matematika-pas.blogspot.com
E-learning Matematika, GRATIS
Tips Mudah Menghitung Perkalian
6 sampai 10 dengan Jari Tangan
Tips menghitung dengan jari ini sudah cukup lama dan lazim diketahui. Teknik ini bahkan tidak hanya dikenal
di Indonesia saja. Tips ini cukup mudah dipraktekkan dan tentu saja cukup praktis, namun keterbatasannya
adalah cara ini hanya dapat dipakai untuk perkalian angka 6 sampai 10. Berikut langkah-langkahnya:
1. Gunakan jari anda dengan tiap jari mewakili angka tertentu, kelingking mewakili angka 6, jari manis =
7, jari tengah = 8, telunjuk adalah 9, dan 10 diwakili oleh jempol.
2. Setiap angka yang akan dikalikan ditandai dengan ditekuk/dilipat. Misalnya 7×8 = maka tekuk 2 jari,
kelingking dan jari manis di tangan satu dan 3 jari, kelingking, jari manis dan jari tengah di tangan
lain(kiri dan kanan sama).
3. Jumlahkan jari-jari yang ditekuk tadi( untuk 7×8 maka jumlah jari yang ditekuk adalah 2+3=5 jari.
Kalikan angka ini dengan sepuluh (5×10=50)
4. Kalikan jari yang tidak ditekuk dari kedua tangan (untuk contoh 7×8 diatas adalah: 3×2=6)
5. Jumlahkan angka yang didapat dari poin (3) dan (4), yaitu 50+6= 56.
6. Cobalah untuk menghitung angka-angka lain dengan catatan bahwa angka hanya boleh untuk angka
6 sampai 10.
Harap diperhatikan bahwa cara ini dipakai hanya untuk mempermudah perkalian. Siswa harus dibekali
pemahaman konsep yang benar dan memadai sebelum diajarkan tips-tips semacam ini
Modul Matematika Teknik Kelas XI SMK