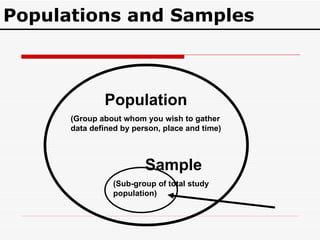
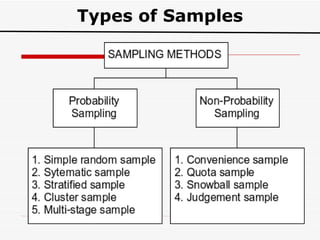
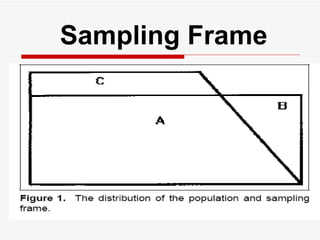
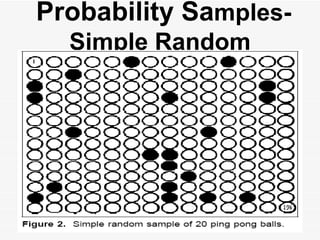
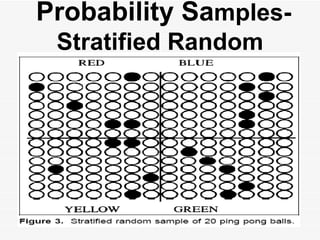
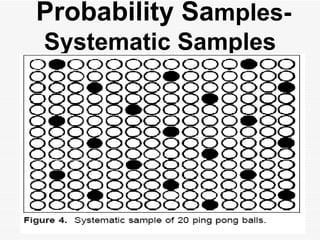
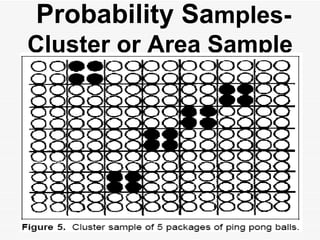
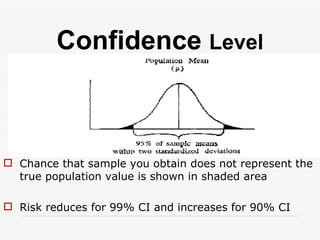
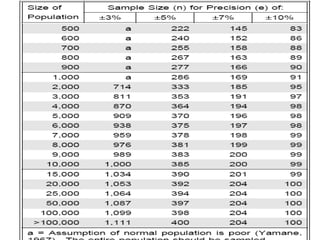
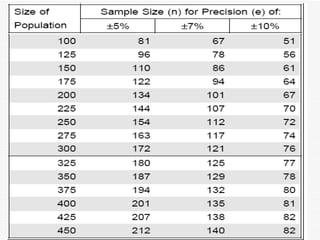
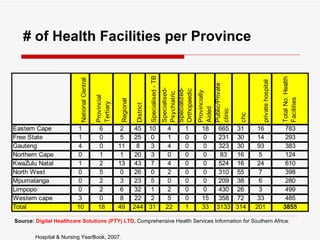
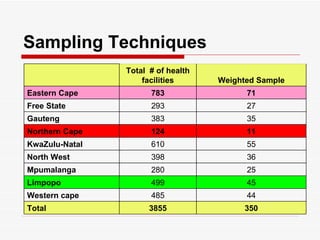
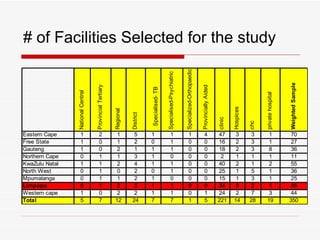
The document discusses the importance of sampling in research, particularly in the context of HIV-associated tuberculosis studies. It outlines various sampling methods, including non-probability and probability samples, and emphasizes the significance of representativity in sample selection to ensure accurate research outcomes. The document also details strategies for determining sample size and criteria for inclusion and exclusion in studies.

1. “ On Samples And Sampling” Title drawn from Elisabeth Kubler-Ross’ anagramatic phraseologies: “On death and dying” ; “On grief and grieving” ; “Real taste of life (On life and living) ” Ehi Igumbor School of Public Health University of the Western Cape

2. “ On Samples ” What is Research all about? Gathering data, information or evidence about a subject or topic What is the outcome of HIV-associated tuberculosis in the era of HAART? But how much data, information or evidence? Should every HIV-associated TB case on HAART be used? Should only 2 be left out? Should 50% of them be used?

3. Populations and Samples Population Larger group to which research results are generalized Defined aggregate of persons, objects, or events that meet a specified set of criteria Sample Sub-group of the population Serves as reference group for estimating characteristics of or drawing conclusions about the population

4. Populations and Samples Population (Group about whom you wish to gather data defined by person, place and time) Sample (Sub-group of total study population)

5. Why use a sample? Save time Save money Save energy Not practical to get everyone Less data so limit error (fewer opportunities to make mistake)– improved quality Why Not? - Just as good!

6. But… Sampling Bias! Are responses of sample members representative of the population? No way to guarantee, but good sampling procedures help Not so much size as representativity: Gallup and Harris polls predicted Nixon win using 2000 voters (43% predicted, 42.9% result) 1936 Literary Digest poll predicted Alf Landon win by 57% based on 2million voters from list of automobile owners and telephone directories

7. Sampling Bias Occurs when individuals selected over- or under- represent certain population attributes that are related to the phenomenon under study May be Conscious or Unconscious

8. Learning Objectives Understand strategies for selecting a sample Understand how to determine the required size of a sample

9. “ On Sampling” – Determining Sampling Procedure What do I want to know? Does self-reported quality of life of patients with HIV-associated tuberculosis improve after HAART compared to before HAART? Is the CD4 count in patients on HAART different from those not on HAART? May involve simply comparing 2 indicators or more rigorous analysis of changes in HAART and not in HAART to estimate the strength of the impact of HAART

10. Determining Sampling Procedure What is my Population? Need a good problem statement Everyone affected (may be geographical, demographical, economic, social, or other specific content of study) Should not be too narrow Sometimes source of data is different from sampling unit e.g household surveys

11. Determining Sampling Procedure Remember Populations are not necessarily restricted human subjects: May include people, places, organizations, objects, animals, days or any unit of interest. E.g Blood samples in an epidemiology study Housing units in a household survey Series of measurements in a test-retest reliability study Inventory of manufactured products in industrial quality control studies

12. Target Population and Accessible Population Study of motor skills Target or reference population: “ ALL children with learning disabilities in South Africa today” Accessible or experimental population “ ALL children identified as having a learning disability in Cape Town’s school system”

13. Inclusion and Exclusion Criteria Inclusion Criteria: primary traits of the target and accessible populations that will qualify someone as a subject Exclusion Criteria: factors that would preclude someone from being studied. (Are potentially confounding to the results)

14. Determining Sampling Procedure To sample or Not to sample? Is it feasible to use population? ?Cost ?Time Sometimes “census” of all needed Small population size Useful to know information on every individual Scope of study: rapid assessment or in-depth investigation

15. Types of Samples

16. Sampling Procedure Non-probability Selection of samples is made by nonrandom methods i.e not based on chance No way to accurately estimate chance of inclusion/degree of sampling error Is convenient and economical Quality depends on knowledge, judgment and expertise of researcher

17. Non-Probability Samples Haphazard Sampling No conscious planning or consistent procedures are employed to select the sample units

18. Non-Probability Samples Convenience or “accidental” Sampling A unit is self-selected (e.g volunteers) or easily accessible/available E.g consecutive sampling of patients Although may yield useful information, caution with making inferences!

19. Non-Probability Samples Quota Sampling A pre-determined number of units which have certain characteristics are selected Controls for confounding effect of known characteristics of a population by selecting adequate numbers from each stratum E.g “50 men and 50 women to be interviewed on a busy street”

20. Non-Probability Samples Snowball Samples Useful if hard to locate subjects with specific characteristics Carried in stages: Select a few subjects who meet selection criteria Ask selected subjects to identify others who have requisite characteristics Repeat process of “chain referral” or “snowballing” till adequate sample size obtained

21. Non-Probability Samples Purposive or judgment Sampling Researcher handpicks subjects on basis of specific characteristics or attributes that are important to the research study Units used sometimes EXTREME or CRITICAL units May be most useful to pre-test an instrument for a larger study or in qualitative studies to ensure subjects have appropriate knowledge and will be good informants for the study

22. Probability Samples Every element in the population has a known, nonzero probability of selection Because probability is known, can be generalized (at least within a given level of precision) to the larger population Risk of incorrectly generalizing to larger population less, thus better than non-probability samples

23. Sampling Frame A list of units or elements from which the sample is to be selected Should list every element separately, once and only once, and nothing else appears on the list Common Problems: Missing elements, non-coverage or incomplete frame Blanks or foreign elements Duplicate listings Clusters of elements combined into one listing

24. Sampling Frame

25. What do you do if a “poor” Sampling Frame? BEFORE SELECTING SAMPLE: Ignore or disregard the problem Redefine population to fit sampling frame Spend time and effort to fix the frame

26. What do you do if a “poor” Sampling Frame? Missing elements: Use supplementary methods. Eg active fieldwork to get homeless individuals in a household based survey Foreign elements: Omit if identified Duplicate elements: Select first, last, current listing Any unique feature? Clusters: Use all. Or randomly select one

27. Probability Sa mples- Simple Random Easiest and least complex Equal chance for each element Using table of random numbers: Assign a number to each element in list Select a starting point Determine number of columns to use Select numbers from table Discard any duplicate you select Select numbers until obtain desired sample size

28. Probability Sa mples- Simple Random

29. Probability Sa mples- Stratified Random Improves on estimates of simple random by random sampling population in strata 3 types: Proportionate Disproportionate or Optimal Equal size

30. Probability Sa mples- Stratified Random

31. Probability Sa mples- Systematic Samples Select first element randomly and then every nth element on the list afterwards Starting point will be a number between 1 and 10 randomly drawn from a table of random numbers Gives each element equal (but not independent) chance Useful if you do not have a list when elements are arranged in space e.g house selection

32. Probability Sa mples- Systematic Samples

33. Probability Sa mples- Cluster or Area Sample A method of selecting sample units in which the unit contains a cluster of elements The probability of selecting an element is a product of the probabilities of selecting its cluster Different from stratified in that ideally, elements are heterogenous. (In stratified they are homogenous) NB: In practice though, clusters tend to be homogenous

34. Probability Sa mples- Cluster or Area Sample

35. PUTTING IT TOGETHER- SELECTING A SAMPLING DESIGN Multi-faceted process Depends on Amount of information available about population If characteristics known – stratified random If little known – less complex simple or systematic When list unavailable – cluster ALSO combined: Stratified multi-staged cluster sampling

36. Determine the type of sampling used A soccer coach selects 6 players from a group of boys aged 8 to 10, 7 players from a group of boys aged 11 to 12, and 3 players from a group of boys aged 13 to 14 to form a recreational soccer team.

37. Determine the type of sampling used A soccer coach selects 6 players from a group of boys aged 8 to 10, 7 players from a group of boys aged 11 to 12, and 3 players from a group of boys aged 13 to 14 to form a recreational soccer team. Stratified

38. Determine the type of sampling used A pollster interviews all human resource personnel in five different high tech companies.

39. Determine the type of sampling used A pollster interviews all human resource personnel in five different high tech companies. Cluster

40. Determine the type of sampling used An engineering researcher interviews 50 women engineers and 50 men engineers.

41. Determine the type of sampling used An engineering researcher interviews 50 women engineers and 50 men engineers. Stratified

42. Determine the type of sampling used A medical researcher interviews every third cancer patient from a list of cancer patients at a local hospital.

43. Determine the type of sampling used A medical researcher interviews every third cancer patient from a list of cancer patients at a local hospital. Systematic

44. Determine the type of sampling used A high school counselor uses a computer to generate 50 random numbers and then picks students whose names correspond to the numbers.

45. Determine the type of sampling used A high school counselor uses a computer to generate 50 random numbers and then picks students whose names correspond to the numbers. Simple random

46. Determine the type of sampling used A student interviews classmates in his algebra class to determine how many pairs of jeans a student owns, on the average.

47. Determine the type of sampling used A student interviews classmates in his algebra class to determine how many pairs of jeans a student owns, on the average. Convenience

48. Suppose UWC has 10,000 part-time students (the population). We are interested in the average amount of money a part-time student spends on books in an academic year. Asking all 10,000 students is an almost impossible task. Suppose we take two different samples.

49. First, we use convenience sampling and survey 10 students from a first semester Masters in Public Health class. Many of these students have been attending the 2009 Summer School and taking elective course on Epidemiology and biostatistics in addition to their MPH core courses . The amount of money they spend is as follows:R128; R87; R173; R116; R130; R204; R147; R189; R93; R153

50. The second sample is taken by using a list from the Division of Life Long Learning unit of adult learners who take part-time classes and taking every 5th student on the list, for a total of 10 students. They spend: R50; R40; R36; R15; R50; R100; R40; R53; R22; R22

51. Problem 1 Do you think that either of these samples is representative of (or is characteristic of) the entire10,000 part-time student population?

52. Problem 2 Since these samples are not representative of the entire population, is it wise to use the results to describe the entire population?

53. Now, suppose we take a third sample. We choose ten different part-time students from all disciplines which offer part-time studies (Public Health, Physio, EMS, etc). Each student is chosen using simple random sampling. Using a calculator, random numbers are generated and a student from a particular discipline is selected if he/she has a corresponding number. The students spend: R180; R50; R150; R85; R260; R75; R180; R200; R200; R150

54. Do you think this sample is representative of the population? Problem 3

55. Learning Objectives Understand strategies for selecting a sample Understand how to determine the required size of a sample

56. Sample Size Determination Determined by: Purpose of study Population size Risk of selecting a “bad” sample Allowable sampling error

57. Sample Size Criteria Level of precision Level of confidence or risk Degree of variability

58. Level of Precision Also called “Sampling error” Range in which the true value of the population is estimated to be So, 42% (+/- 2%): 40% - 44%

59. Confidence Level Also called “Risk level” Based on principle of Central Limit Theorem 95% CI – 95 out of 100 samples will have the true population value within the range of precision specified

60. Confidence Level Chance that sample you obtain does not represent the true population value is shown in shaded area Risk reduces for 99% CI and increases for 90% CI

61. Degree of Variability Distribution of attributes Heterogenous – bigger sample Homogenous – smaller sample Note that 50% indicates a greater level of variability than 20% and 80% 0.5 is mostly used in conservative samples because it indicates maximum variability

62. Strategies for determining Sample Size Using a Census for small populations Using a Sample Size of a Similar Study Using Published Tables Using Formula to Calculate a Sample Size

63. Using a Census for small populations Use entire population as sample May be useful in Small population cost permitting (<200) Why use this? Eliminates sampling error Provides individual level data “ Fixed costs” eg of questionnaire design etc Virtually entire population would have to be in sample in small populations anyway

64. Using a Sample Size of a Similar Study Could be a valuable approach But without reviewing the procedures employed, may run risk of repeating errors made previously Review literature to get guidance on “typical” sample size

65. Using Published Tables Use published tables which provide sample size for a given set of criteria Sample sizes in tables reflect the number of OBTAINED responses (not necessarily the number of surveys mailed ) Assumptions of normality in distribution

68. Using Formulas to Calculate A Sample Size  Equation 2: (Snedecor & Cochran 1989)  Equation 1: (Fleiss 1981)  Equation 3: (Yamane’s 1967)

69. Other Considerations Assumes simple random sampling Number needed for data analysis (eg multiple regression analysis, log linear analysis require a bigger sample than if simple descriptive analysis) Sample size increased by 30% to compensate for non-response; 10% to compensate for persons unable to reach

70. Calculation Using Computer Programmes Epi Info Online Softwares: eg Rao Soft

71. EXAMPLE: Sample Size Calculation Where n = Sample size N = Population size e = Level of precision or Sampling of Error which is ± 5% Yamane’s formula: * Reference: Yamane, Taro. 1967. Statistics, An Introductory Analysis,2 nd Ed. New York: Harper and Row.

72. # of Health Facilities per Province Source: Digital Healthcare Solutions (PTY) LTD . Comprehensive Health Services Information for Southern Africa: Hospital & Nursing YearBook, 2007.

73. Sample Size Calculation: Total number of health facilities in the study: 350 *Reference: Yamane, Taro. 1967. Statistics, An Introductory Analysis,2 nd Ed. New York: Harper and Row.

74. Sampling Techniques Multi-Stage Sampling Primary sampling unit Stratification by district (Selection Bias) Levels of Care Rural/Urban Sample Proportional Size Sampling Weight:

75. Sampling Techniques Total # of health facilities Weighted Sample Eastern Cape 783 71 Free State 293 27 Gauteng 383 35 Northern Cape 124 11 KwaZulu-Natal 610 55 North West 398 36 Mpumalanga 280 25 Limpopo 499 45 Western cape 485 44 Total 3855 350

76. # of Facilities Selected for the study

77. BIBLIOGRAPHY Israel GD. (1992) Sampling the evidence of extension program impact. University of Florida IFAS Extension PEOD5. (http://edis.ifas.ufl.edu.) Israel GD. (1992) Determining Sample Size. University of Florida IFAS Extension PEOD6 (http://edis.ifas.ufl.edu.) Portney LG and Watkins MP. (2000). Foundations of clinical research – applications to practice. 2 nd Ed. Chapter 8 - Sampling “ I have collected a poesy of another man’s roses, and nothing but the thread that binds them together is my own”