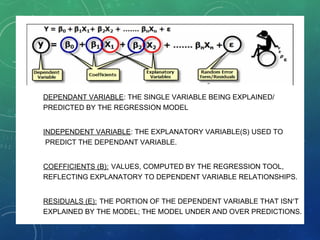
This presentation introduces regression analysis. It discusses key concepts such as dependent and independent variables, simple and multiple regression, and linear and nonlinear regression models. It also covers different types of regression including simple linear regression, cross-sectional vs time series data, and methods for building regression models like stepwise regression and forward/backward selection. Examples are provided to demonstrate calculating regression equations using the least squares method and computing deviations from mean values.

1. WELCOME TO OUR PRESENTATION
PRESENTED BY:
Md . Sohag
Em@il : sohag.0315@gmail.com
Daffodil international University

3. INTRODUCTION. . .
• FATHER OF REGRESSION ANALYSIS
CARL F. GAUSS (1777-1855).
• CONTRIBUTIONS TO PHYSICS, MATHEMATICS &
ASTRONOMY.
• THE TERM “REGRESSION” WAS FIRST USED IN
1877 BY FRANCIS GALTON.

4. REGRESSION ANALYSIS. . .
• IT IS THE STUDY OF THE
RELATIONSHIP BETWEEN
VARIABLES.
• IT IS ONE OF THE MOST
COMMONLY USED TOOLS FOR
BUSINESS ANALYSIS.
• IT IS EASY TO USE AND APPLIES
TO MANY SITUATIONS.

5. REGRESSION TYPES. . .
• SIMPLE REGRESSION: SINGLE
EXPLANATORY VARIABLE
• MULTIPLE REGRESSION: INCLUDES ANY
NUMBER OF EXPLANATORY VARIABLES.

6. • DEPENDANT VARIABLE: THE SINGLE VARIABLE BEING EXPLAINED/
• PREDICTED BY THE REGRESSION MODEL
• INDEPENDENT VARIABLE: THE EXPLANATORY VARIABLE(S) USED TO
• PREDICT THE DEPENDANT VARIABLE.
• COEFFICIENTS (Β): VALUES, COMPUTED BY THE REGRESSION TOOL,
• REFLECTING EXPLANATORY TO DEPENDENT VARIABLE RELATIONSHIPS.
• RESIDUALS (Ε): THE PORTION OF THE DEPENDENT VARIABLE THAT ISN’T
• EXPLAINED BY THE MODEL; THE MODEL UNDER AND OVER PREDICTIONS.

7. REGRESSION ANALYSIS. . .
• LINEAR REGRESSION: STRAIGHT-LINE
RELATIONSHIP
– Form: y=mx+b
• NON-LINEAR: IMPLIES CURVED RELATIONSHIPS
–
logarithmic relationships

8. REGRESSION ANALYSIS. . .
• CROSS SECTIONAL: DATA GATHERED FROM THE
SAME TIME PERIOD
• TIME SERIES: INVOLVES DATA OBSERVED OVER
EQUALLY SPACED POINTS IN TIME.

9. SIMPLE LINEAR REGRESSION MODEL. . .

10. TYPES OF REGRESSION MODELS. . .

11. xbbyˆ 10i +=
The sample regression line provides an estimate of
the population regression line
ESTIMATED REGRESSION MODEL. . .
Estimate of
the regression
intercept
Estimate of the
regression slope
Estimated
(or predicted)
y value
Independent
variable
The individual random error terms ei have a mean of zero

12. REGRESSION ANALYSIS: MODEL BUILDINGREGRESSION ANALYSIS: MODEL BUILDING
General Linear Model
Determining When to Add or Delete Variables
Analysis of a Larger Problem
Multiple Regression Approach
to Analysis of Variance

13. GENERAL LINEAR MODELGENERAL LINEAR MODEL
Modelsin which theparameters(β0, β1, . . . , βp) all haveexponentsof onearecalled
linear models.
 First-Order Model with OnePredictor Variable
y x= + +β β ε0 1 1y x= + +β β ε0 1 1

14. VARIABLE SELECTION PROCEDURESVARIABLE SELECTION PROCEDURES
Stepwise Regression
Forward Selection
Backward Elimination
Iterative; one independent
variable at a time is
added or
deleted
Based on
the F statistic

15. VARIABLE SELECTION PROCEDURESVARIABLE SELECTION PROCEDURES
F Test
To test whether the addition of x2 to a
model involving x1 (or the deletion of x2
from a model involving x1and x2) is
statistically significant
F0=MSR/MSRes
(MSR=SSR/K)
The p-value corresponding to the F statistic
is the criterion used to determine if a variable
should be added or deleted
(SSE(reduced)-SSE(full))/number of extra terms
MSE(full)
F =

16. FORWARD SELECTIONFORWARD SELECTION
This procedure is similar to stepwise-regression,
but does not permit a variable to be deleted.
This forward-selection procedure starts with no
independent variables.
It adds variables one at a time as long as a
significant reduction in the error sum of squares
(SSE) can be achieved.

17. BACKWARD ELIMINATIONBACKWARD ELIMINATION
This procedure begins with a model that includes all the
independent variables the modeler wants considered.
It then attempts to delete one variable at a time by
determining whether the least significant variable currently
in the model can be removed because its p-value is less than
the user-specified or default value.
Once a variable has been removed from the model it cannot
re enter at a subsequent step.

18. Example1-:From the following data obtain the two regression equations
using the method of Least Squares.
X 3 2 7 4 8
Y 6 1 8 5 9
Solution-:
X Y XY X2
Y2
3 6 18 9 36
2 1 2 4 1
7 8 56 49 64
4 5 20 16 25
8 9 72 64 81
∑ = 24X ∑ = 29Y ∑ =168XY 1422
=∑ X 2072
=∑Y

19. Example2-: from the previous data obtain the regression equations by
Taking deviations from the actual means of X and Y series.
X 3 2 7 4 8
Y 6 1 8 5 9
X Y x2
y2
xy
3 6 -1.8 0.2 3.24 0.04 -0.36
2 1 -2.8 -4.8 7.84 23.04 13.44
7 8 2.2 2.2 4.84 4.84 4.84
4 5 -0.8 -0.8 0.64 0.64 0.64
8 9 3.2 3.2 10.24 10.24 10.24
XXx −= YYy −=
∑ = 24X ∑ = 29Y 8.26
2
=∑x 8.28=∑ xy8.382
=∑ y∑ = 0x 0∑ =y
Solution-:

20. Example-: From the data given in previous example calculate regression
equations by assuming 7 as the mean of X series and 6 as the mean of Y series.
X Y
Dev. From
assu.
Mean 7
(dx)=X-7
Dev. From
assu. Mean
6 (dy)=Y-6 dxdy
3 6 -4 16 0 0 0
2 1 -5 25 -5 25 +25
7 8 0 0 2 4 0
4 5 -3 9 -1 1 +3
8 9 1 1 3 9 +3
Solution-:
2
xd 2
yd
∑ = 24X ∑ = 29Y ∑ −= 11xd ∑ −= 1yd∑ = 512
xd ∑ = 392
yd ∑ = 31yxdd