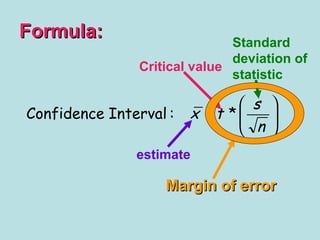
- Confidence intervals provide an estimated range of values that is likely to include an unknown population parameter, such as a mean, with a specified degree of confidence. - The margin of error depends on the sample size, standard deviation, and confidence level, with a larger sample size and smaller standard deviation yielding a smaller margin of error. - When the sample size is small, a t-distribution rather than normal distribution is used to construct the confidence interval due to the unknown population standard deviation. The t-distribution is wider than the normal and accounts for additional uncertainty from an unknown standard deviation.

1. Confidence
Intervals

2. Rate your confidenceRate your confidence
0 - 1000 - 100
• Guess my age within 10 years?
• within 5 years?
• within 1 year?
• Shooting a basketball at a wading pool, will
make basket?
• Shooting the ball at a large trash can, will
make basket?
• Shooting the ball at a carnival, will make
basket?

3. What happens to your
confidence as the interval
gets smaller?
The smaller the interval, the
lower your confidence.
%%
%%
%%
%%

4. Point Estimate
• Use a singlesingle statistic based on
sample data to estimate a
population parameter
• Simplest approach
• But not always very precise due to
variationvariation in the sampling
distribution

5. Confidence intervalsConfidence intervals
• Are used to estimate the
unknown population mean
• Formula:
estimate + margin of error

6. Margin of errorMargin of error
• Shows how accurate we believe our
estimate is
• The smaller the margin of error, the
more precisemore precise our estimate of the true
parameter
• Formula:






⋅





=
statistictheof
deviationstandard
value
critical
m

7. Confidence levelConfidence level
• Is the success rate of the method
used to construct the interval
• Using this method, ____% of the
time the intervals constructed will
contain the true population
parameter

8. • Found from the confidence level
• The upper z-score with probability p lying to
its right under the standard normal curve
Confidence level tail area z*
.05 1.645
.025 1.96
.005 2.576
Critical value (z*)Critical value (z*)
.05
z*=1.645
.025
z*=1.96
.005
z*=2.576
90%
95%
99%

9. Confidence interval for aConfidence interval for a
population mean:population mean:






±
n
zx
σ
*
estimate
Critical
value
Standard
deviation of the
statistic
Margin of error

10. What does it mean to be 95%What does it mean to be 95%
confident?confident?
• 95% chance that µ is contained in
the confidence interval
• The probability that the interval
contains µ is 95%
• The method used to construct the
interval will produce intervals that
contain µ 95% of the time.

11. Steps for doing a confidenceSteps for doing a confidence
interval:interval:
1) Assumptions –
• SRS from population (or randomly assigned
treatments)
• Sampling distribution is normal (or approximately
normal)
• Given (normal)
• Large sample size (approximately normal)
• Graph data (approximately normal)
• σ is known
1) Calculate the interval
2) Write a statement about the interval in the
context of the problem.

12. Statement:Statement: (memorize!!)(memorize!!)
We are ________% confident
that the true mean context lies
within the interval ______ and
______.

13. Assumptions:
Have an SRS of blood measurements
Potassium level is normally distributed (given)
σ known
We are 90% confident that the true mean
potassium level is between 3.01 and 3.39.
A test for the level of potassium in the blood
is not perfectly precise. Suppose that
repeated measurements for the same
person on different days vary normally with
σ = 0.2. A random sample of three has a
mean of 3.2. What is a 90% confidence
interval for the mean potassium level?
( )3899.3,0101.3
3
2.
645.12.3 =





±

14. Assumptions:
Have an SRS of blood measurements
Potassium level is normally distributed
(given)
σ known
We are 95% confident that the true mean
potassium level is between 2.97 and
3.43.
95% confidence interval?
( )4263.3,9737.2
3
2.
96.12.3 =





±

15. 99% confidence interval?
Assumptions:
Have an SRS of blood measurements
Potassium level is normally distributed
(given)
σ known
We are 99% confident that the true mean
potassium level is between 2.90 and 3.50.
( )4974.3,9026.2
3
2.
576.22.3 =





±

16. What happens to the interval as theWhat happens to the interval as the
confidence level increases?confidence level increases?
the interval gets wider as the
confidence level increases

17. How can you make the margin ofHow can you make the margin of
error smaller?error smaller?
• z* smaller
(lower confidence level)
• σ smaller
(less variation in the population)
• n larger
(to cut the margin of error in half, n must
be 4 times as big)
Really cannot
change!

18. A random sample of 50 PHS students was
taken and their mean SAT score was 1250.
(Assume σ = 105) What is a 95% confidence
interval for the mean SAT scores of PHS
students?
Assume: Given SRS of students;
distribution is approximately normal due
to large sample size; σ known
We are 95% confident that the true mean
SAT score for PHS students is between
1220.9 and 1279.1

19. Suppose that we have this random sample
of SAT scores:
950 1130 1260 1090 1310 1420 1190
What is a 95% confidence interval for the
true mean SAT score? (Assume σ = 105)
Assume: Given SRS of students; distribution is
approximately normal because the boxplot is
approximately symmetrical; σ known
We are 95% confident that the true mean SAT
score for PHS students is between 1115.1 and
1270.6.

20. Find a sample size:Find a sample size:






=
n
zm
σ
*
• If a certain margin of error is wanted,
then to find the sample size necessary
for that margin of error use:
Always round up to the nearest person!

21. The heights of BCP male students is
normally distributed with σ = 2.5
inches. How large a sample is
necessary to be accurate within + .75
inches with a 95% confidence
interval?
n = 43

22. In a randomized comparative experiment
on the effects of calcium on blood
pressure, researchers divided 54 healthy,
white males at random into two groups,
takes calcium or placebo. The paper
reports a mean seated systolic blood
pressure of 114.9 with standard deviation
of 9.3 for the placebo group. Assume
systolic blood pressure is normally
distributed.
Can you find a z-interval for thisCan you find a z-interval for this
problem? Why or why not?problem? Why or why not?

23. Student’s t- distributionStudent’s t- distribution
• Developed by William Gosset
• Continuous distribution
• Unimodal, symmetrical, bell-shaped
density curve
• Above the horizontal axis
• Area under the curve equals 1
• Based on degrees of freedom

24. Graph examples of t- curves vs normal
curve

25. How doesHow does tt compare tocompare to
normal?normal?
• Shorter & more spread out
• More area under the tails
• As n increases, t-distributions
become more like a standard
normal distribution

26. How to findHow to find tt**
• Use Table B for t distributions
• Look up confidence level at bottom &
df on the sides
• df = n – 1
Find these t*
90% confidence when n = 5
95% confidence when n = 15
t* =2.132
t* =2.145

27. Formula:Formula:






±
n
s
tx *:IntervalConfidence
estimate
Critical value
Standard
deviation of
statistic
Margin of errorMargin of error

28. Assumptions forAssumptions for tt-inference-inference
• Have an SRS from population (or
randomly assigned treatments)
• σ unknown
• Normal (or approx. normal) distribution
– Given
– Large sample size
– Check graph of data

29. For the Ex. 4: Find a 95% confidence
interval for the true mean systolic
blood pressure of the placebo group.
Assumptions:
• Have randomly assigned males to treatment
• Systolic blood pressure is normally distributed
(given).
• σ is unknown
We are 95% confident that the true mean systolic
blood pressure is between 111.22 and 118.58.
)58.118,22.111(
27
3.9
056.29.114 =





±

30. RobustRobust
• An inference procedure is ROBUST if
the confidence level or p-value doesn’t
change much if the assumptions are
violated.
• t-procedures can be used with some
skewness, as long as there are no
outliers.
• Larger n can have more skewness.
Since there is more area in the tails in t-
distributions, then, if a distribution has
some skewness, the tail area is not
greatly affected.
CI & p-values deal with area in the
tails – is the area changed greatly
when there is skewness

31. Ex. 5 – A medical researcher measured
the pulse rate of a random sample of 20
adults and found a mean pulse rate of
72.69 beats per minute with a standard
deviation of 3.86 beats per minute.
Assume pulse rate is normally
distributed. Compute a 95% confidence
interval for the true mean pulse rates of
adults.
We are 95% confident that the true mean
pulse rate of adults is between 70.883 &
74.497.

32. Another medical researcher claims that
the true mean pulse rate for adults is 72
beats per minute. Does the evidence
support or refute this? Explain.
The 95% confidence interval contains
the claim of 72 beats per minute.
Therefore, there is no evidence to doubt
the claim.

33. Ex. 6 – Consumer Reports tested 14
randomly selected brands of vanilla
yogurt and found the following
numbers of calories per serving:
160 200 220 230 120 180 140
130 170 190 80 120 100 170
Compute a 98% confidence interval for
the average calorie content per serving
of vanilla yogurt.
We are 98% confident that the true mean calorie
content per serving of vanilla yogurt is between
126.16 calories & 189.56 calories.

34. A diet guide claims that you will get 120
calories from a serving of vanilla
yogurt. What does this evidence
indicate?
Since 120 calories is not contained
within the 98% confidence interval, the
evidence suggest that the average
calories per serving does not equal 120
calories.
Note: confidence intervals tell
us if something is NOT EQUALNOT EQUAL
– never less or greater than!

35. Some Cautions:Some Cautions:
• The data MUST be a SRS from the
population (or randomly assigned
treatment)
• The formula is not correct for more
complex sampling designs, i.e.,
stratified, etc.
• No way to correct for bias in data

36. Cautions continued:Cautions continued:
• Outliers can have a large effect on
confidence interval
• Must know σ to do a z-interval –
which is unrealistic in practice