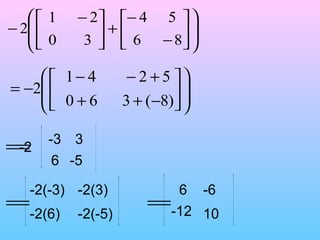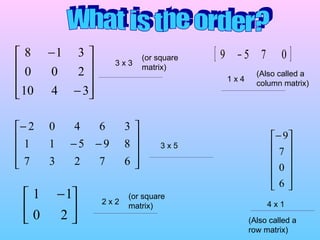
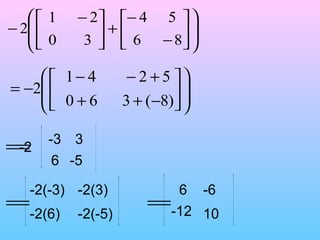
This document discusses basic matrix operations including: - Defining a matrix as a rectangular arrangement of numbers in rows and columns with an order specified by the number of rows and columns. - Adding and subtracting matrices requires they have the same order and involves adding or subtracting corresponding entries. - Multiplying a matrix by a scalar involves multiplying each entry in the matrix by the scalar value. - Matrix multiplication is not commutative and can only be done if the number of columns in the first matrix equals the number of rows in the second matrix. It involves multiplying entries and summing the products based on their positions.

1. Matrix Operations

3. What is the order? 3 x 3 3 x 5 2 x 2 4 x 1 1 x 4 (or square matrix) (Also called a row matrix) (or square matrix) (Also called a column matrix)

5. = = 7 7 4 5 0 7 5 7

7. = 5-2 -4-1 3-8 8-3 0-(-1) -7-1 1-(-4) 2-0 0-7 = 2 -5 -5 5 1 -8 5 3 -7

9. -2 6 -3 3 -2(-3) -5 -2(6) -2(-5) -2(3) 6 -6 -12 10