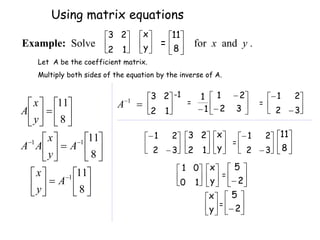
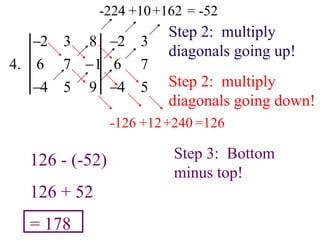
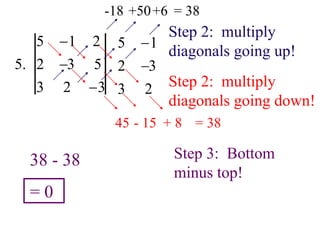
This document provides an introduction to matrices and determinants. Some key points: - Matrices are arrays of numbers arranged in rows and columns. Determinants are single numbers associated with square matrices. - Methods are presented for calculating the determinants of 2x2 and 3x3 matrices, including the diagonal and cofactor methods. - The determinant of a matrix is used to find the inverse of a matrix and in calculating the area of triangles. - Matrix operations like multiplication and solving systems of equations can be represented using matrix notation. The inverse of a matrix allows solving systems of equations written in matrix form.

1. Determinants

2. Matrices
• A matrix is an array of
numbers that are
arranged in rows and
columns.
• A matrix is “square” if
it has the same number
of rows as columns.
• We will consider only
2x2 and 3x3 square
matrices
0
-½
3
1
11
180
4
-¾
0
2
¼
8
-3

3. Determinants
• Every square matrix has
a determinant.
• The determinant of a
matrix is a number.
• We will consider the
determinants only of
2x2 and 3x3 matrices.
1 3
-½ 0
-3 8 ¼
2 0 -¾
4 180 11
Note the difference in the matrix
and the determinant of the
matrix!

4. Why do we need the determinant
• It is used to help us
calculate the inverse
of a matrix and it is
used when finding
the area of a triangle

5. Find the determinant:
1.
5 7
11 8 5 8
  7
 11
 
  40  77
 
 37
40  77
2.
3 2
1 5
 3 5
  2
  1
  15 2
 
 17
15 2

6. 3.
10 2
0 3
 10(-3)-(-2)(0)
 -30+ 0 = -30
Finding a 3x3 determinant: Diagonal method
4.
2 3 8
6 7 1
4 5 9
Step 1: Rewrite first two
rows of the matrix.

7. 4.
2 3 8
6 7 1
4 5 9
2 3
6 7
4 5
Step 2: multiply
diagonals going up!
-224 +10+162 = -52
Step 2: multiply
diagonals going down!
-126 +12+240 =126
Step 3: Bottom
minus top!
126 - (-52)
126 + 52
= 178

8. 5.
5 1 2
2 3 5
3 2 3
Step 2: multiply
diagonals going up!
-18 +50+6 = 38
Step 2: multiply
diagonals going down!
45 - 15 + 8 = 38
Step 3: Bottom
minus top!
38 - 38
= 0
5 1
2 3
3 2

9. 4
5
2
3

(3 * 4) - (-5 * 2)
12 - (-10)
22
=
4
5
2
3

Finding Determinants of Matrices
=
=

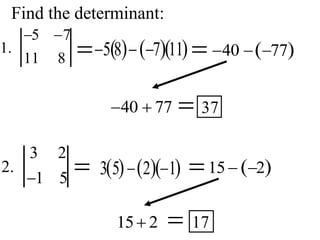
10. 2
4
1
5
2
1
3
0
2


2
1
-1
0
-2
4
= [(2)(-2)(2) + (0)(5)(-1) + (3)(1)(4)]
[(3)(-2)(-1) + (2)(5)(4) + (0)(1)(2)]
[-8 + 0 +12]
-
- [6 + 40 + 0]
4 – 6 - 40
Finding Determinants of Matrices
=
= = -42

11. 





1
0
0
1
Identity matrix: Square matrix with 1’s on the diagonal
and zeros everywhere else
2 x 2 identity matrix










1
0
0
0
1
0
0
0
1
3 x 3 identity matrix
The identity matrix is to matrix multiplication as
___ is to regular multiplication!!!!
1
Using matrix equations

12. Multiply:






1
0
0
1





 
4
3
2
5
= 




 
4
3
2
5






1
0
0
1





 
4
3
2
5
= 




 
4
3
2
5
So, the identity matrix multiplied by any matrix
lets the “any” matrix keep its identity!
Mathematically, IA = A and AI = A !!

13. Inverse Matrix:
Using matrix equations
2 x 2






d
c
b
a
In words:
•Take the original matrix.
•Switch a and d.
•Change the signs of b and c.
•Multiply the new matrix by 1 over the determinant of the original matrix.








 a
c
b
d
bc
ad
1

1
A

A

14. 




 



 2
4
4
10
)
4
)(
4
(
)
10
)(
2
(
1





 

 2
4
4
10
4
1
=












2
1
1
1
2
5
Using matrix equations
Example: Find the inverse of A.







 10
4
4
2

A

1
A

1
A

15. Find the inverse matrix.








2
5
3
8
Det A = 8(2) – (-5)(-3) = 16 – 15 = 1
Matrix A
Inverse =










det
1 Matrix
Reloaded






8
5
3
2
1
1
= = 





8
5
3
2

16. What happens when you multiply a matrix by its inverse?
1st: What happens when you multiply a number by its inverse?
7
1
7 
A & B are inverses. Multiply them.






8
5
3
2
=








2
5
3
8






1
0
0
1
So, AA-1
= I

17. Why do we need to know all this? To Solve Problems!
Solve for Matrix X.
=








2
5
3
8
X 







1
3
1
4
We need to “undo” the coefficient matrix. Multiply it by its INVERSE!






8
5
3
2
=








2
5
3
8
X 





8
5
3
2








1
3
1
4






1
0
0
1
X = 







3
4
1
1
X =








3
4
1
1

18. You can take a system of equations and write it with
matrices!!!
3x + 2y = 11
2x + y = 8
becomes 





1
2
2
3






y
x
= 





8
11
Coefficient
matrix
Variable
matrix
Answer matrix
Using matrix equations

19. Let A be the coefficient matrix.
Multiply both sides of the equation by the inverse of A.










































8
11
8
11
8
11
1
1
1
A
y
x
A
y
x
A
A
y
x
A 





1
2
2
3 -1
= 







 3
2
2
1
1
1
= 







3
2
2
1








3
2
2
1






1
2
2
3






y
x
= 







3
2
2
1






8
11






1
0
0
1






y
x
= 





 2
5






y
x
= 





 2
5
Using matrix equations






1
2
2
3






y
x
= 





8
11
Example: Solve for x and y .

1
A

20. Wow!!!!
3x + 2y = 11
2x + y = 8
x = 5; y = -2
3(5) + 2(-2) = 11
2(5) + (-2) = 8
It works!!!!
Using matrix equations
Check:

21. You Try…
Solve:
4x + 6y = 14
2x – 5y = -9
(1/2, 2)

22. You Try…
Solve:
2x + 3y + z = -1
3x + 3y + z = 1
2x + 4y + z = -2
(2, -1, -2)