The document defines matrices and matrix operations such as addition, subtraction and scalar multiplication. It provides examples of using matrices to organize data on students' wins and losses in a chess competition. It also discusses rules for matrix multiplication, including that the number of columns in the first matrix must equal the number of rows in the second matrix for the product to be defined. Examples are provided to illustrate solving systems of equations using matrix addition and multiplication.


![ Rows x columns
Read rows by columns
Rows go across
Columns go down
[ 1 2 3 4 ] 1 x 4 matrix](https://image.slidesharecdn.com/matrix1-110208131820-phpapp02/75/Matrices-Chapter-4-Obj-1-04-2-10-3-2048.jpg)













![ X - [ 1 1]= [0 1]
[ 3 2] [ 89]
Enter the 2nd matrix as A
since it is not going to
move.
Enter the 1 matrix as B.
st](https://image.slidesharecdn.com/matrix1-110208131820-phpapp02/75/Matrices-Chapter-4-Obj-1-04-2-10-17-2048.jpg)

![ [4] [3 4 7 ]
[6]
[8]
Equal matrices?
Why or why not?](https://image.slidesharecdn.com/matrix1-110208131820-phpapp02/75/Matrices-Chapter-4-Obj-1-04-2-10-19-2048.jpg)
![ [ -2 3 ] [ -8/4
6-3 ]
[ 5 0] [ 15/3
4-4]
Equal matrices?
Why or why not?](https://image.slidesharecdn.com/matrix1-110208131820-phpapp02/75/Matrices-Chapter-4-Obj-1-04-2-10-20-2048.jpg)

![ [x+8 -5 ] = [ 38
-5 ]
[ 3 -y ] [3
4y-10]](https://image.slidesharecdn.com/matrix1-110208131820-phpapp02/75/Matrices-Chapter-4-Obj-1-04-2-10-22-2048.jpg)
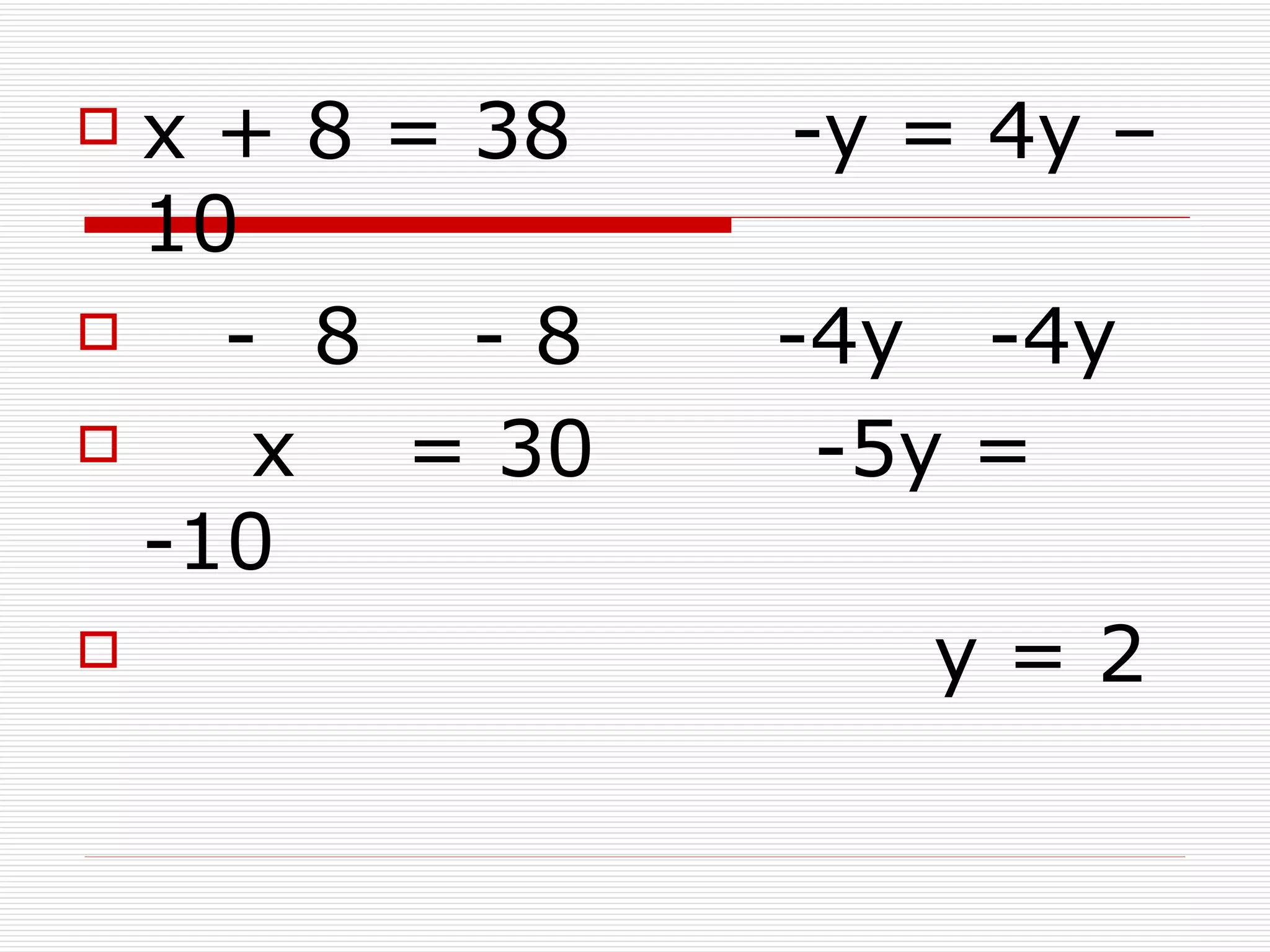
![ [ 3x 4] = [ -9 x
+y]](https://image.slidesharecdn.com/matrix1-110208131820-phpapp02/75/Matrices-Chapter-4-Obj-1-04-2-10-24-2048.jpg)



![ 3[2 6]
[7 4]](https://image.slidesharecdn.com/matrix1-110208131820-phpapp02/75/Matrices-Chapter-4-Obj-1-04-2-10-28-2048.jpg)


![ -3y + 2 [ 6 9 ] = [ 27
-18 ]
[ -12 15] [ 30
6 ]](https://image.slidesharecdn.com/matrix1-110208131820-phpapp02/75/Matrices-Chapter-4-Obj-1-04-2-10-31-2048.jpg)
![ 2x = [ 4 12 ] + [ -2
0]
[ 1 -4] [ 3
4]](https://image.slidesharecdn.com/matrix1-110208131820-phpapp02/75/Matrices-Chapter-4-Obj-1-04-2-10-32-2048.jpg)
![ -3x + [ 7 0 -1 ] = [ 10
0 8]
[2 -3 4] [-19
-18 10]](https://image.slidesharecdn.com/matrix1-110208131820-phpapp02/75/Matrices-Chapter-4-Obj-1-04-2-10-33-2048.jpg)




![ [ -2 5] [ 4 -4 ]
[3 -1] [2 6]
A has 2 rows and 2
columns.
B has 2 rows and 2
columns.
The col. Of A = the rows of](https://image.slidesharecdn.com/matrix1-110208131820-phpapp02/75/Matrices-Chapter-4-Obj-1-04-2-10-38-2048.jpg)
![ [ 10 ] [ 12 3]
[ -5 ]
[1 2] [ 7 6 8 13 ]
[3 4] [ 9 10 11 19]](https://image.slidesharecdn.com/matrix1-110208131820-phpapp02/75/Matrices-Chapter-4-Obj-1-04-2-10-39-2048.jpg)
![ [ w x ] [ 9 -7 ]
[ y z ] [3 1]
[ -3 5] [ -3 ]
[ 5]](https://image.slidesharecdn.com/matrix1-110208131820-phpapp02/75/Matrices-Chapter-4-Obj-1-04-2-10-40-2048.jpg)
