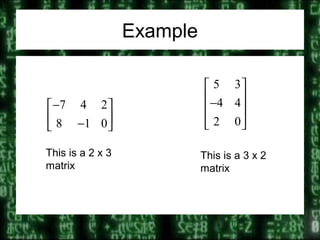
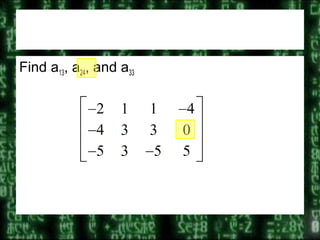
A matrix is a rectangular array of numbers arranged in rows and columns. The dimensions of a matrix are written as the number of rows x the number of columns. Each individual entry in the matrix is named by its position, using the matrix name and row and column numbers. Matrices can represent systems of equations or points in a plane. Operations on matrices include addition, multiplication by scalars, and dilation of points represented by matrices.

1. Matrices
A matrix is a rectangular array of numbers
arranged in rows and columns.
The dimensions of a matrix are written as
rows x columns.
Count AcrossCount
Down

2. Example
5 3
4 4
2 0
 
 − 
  
7 4 2
8 1 0
− 
 − 
This is a 2 x 3
matrix
This is a 3 x 2
matrix

3. Naming Matrices
A capital letter is used to name a matrix.
Each individual entry is named by its
position in the matrix.
11 12 13 14 15
21 22 23 24 25
31 32 33 34 35
a a a a a
a a a a a
a a a a a
 
 
 
  

4. Find a13, a24, and a33

5. Find a13, a24, and a33

6. Find a13, a24, and a33

7. Find a13, a24, and a33

8. Special Matrices
A matrix with the same number of columns
and rows (2 x 2, 3 x 3, etc.) is called a
square matrix.
A matrix with all zeros is called a zero
matrix.

9. Equal Matrices
Two matrices are equal if:
They have the same dimensions
The corresponding entries are equal
7 8
7 8
1
16 0.5 4
2
7 4
7 4
 
  
   =   
 −  − 
Each pair is equal:
7 = 7
8 = 8
½ = 0.5
Etc.

10. Using Equal Matrices
Equal matrices can be used to solve for
variables.
2
3 4 2
3 9 3
7 4 7 4
x y
z
+   
   =   
   − −   
Set up each equation
separately with
corresponding entries
3 = x
4 = y +2 (y = 2)
z2
= 9 (z =+3 or -3)

11. Try these

13. Scalar Multiplication
Matrices can be multiplied by a single
number called a scalar. In scalar
multiplication, multiply everything in the
matrix by that number.
2 6 6 18
3
4 1 12 3
   
=   − −   

14. Representing Points
Points can be represented in a matrix.
A matrix for the points (3,5); (-2,4); and (1,-1)
would look like this:
3 2 1
5 4 1
− 
 − 
x on the top
y on the bottom

15. Dilation
Multiplying a matrix of points by a scalar
represents a dilation of the figure.
(Dilations make the shape bigger or
smaller)

16. Example
What are the new coordinates if the this
triangle has a dilation factor of 3?
The new coordinates are (9,15); (-6,12); (3, -3)
3 2 1 9 6 3
3
5 4 1 15 12 3
− −   
=   − −   