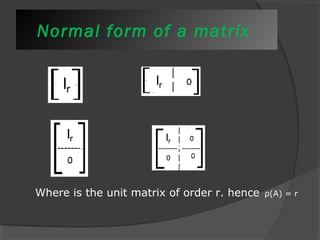
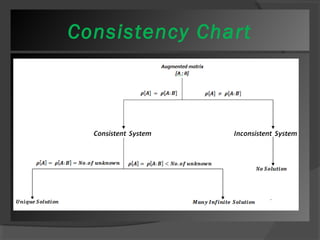
This document provides an overview of matrix mathematics concepts. It discusses how matrices are useful in engineering calculations for storing values, solving systems of equations, and coordinate transformations. The outline then reviews properties of matrices and covers various matrix operations like addition, multiplication, and transposition. It also defines different types of matrices and discusses determining the rank, inverse, eigenvalues and eigenvectors of matrices. Key matrix algebra topics like solving systems of equations and putting matrices in normal form are summarized.

1. MOHAMMAD IMRAN
DEPARTMENT OF APPLIED SCIENCES
JAHANGIRABAD EDUCATIONAL GROUP OF INSTITUTES
www.jit.edu.in

2. Matrix Mathematics
• Matrices are very useful in engineering
calculations. For example, matrices are used to:
– Efficiently store a large number of values (as we have
done with arrays in MATLAB)
– Solve systems of linear simultaneous equations
– Transform quantities from one coordinate system to
another
• Several mathematical operations involving
matrices are important

3. Outline
 Basics:
Operations on matrices
 Transpose of the matrices
 Types of matrices
 Determinant of matrix
 Linear systems of algebraic equations
Matrix rank, existence of a solution
Inverse of a matrix
Normal form of the matrix
Rank of matrix by using the normal form
 Non-singular matrices P & Q which makes normal form with given matrix A
as PAQ

4. Outline cont’
 Consistency
 Eigen values and Eigenvectors

5. Review: Properties of Matrices
• A matrix is a one-or two dimensional array
• A quantity is usually designated as a matrix by bold face
type: A
• The elements of a matrix are shown in square brackets:

6. Review: Properties of Matrices cont.
• The dimension (size) of a matrix is defined by the
number of rows and number of columns
• Examples:
3 × 3: 2×4:

7. Review: Properties of Matrices cont.
• An element of a matrix is usually written in lower
case, with its row number and column number as
subscripts :

8. Matrix Operations
• Matrix Addition
• Multiplication of a Matrix by a Scalar
• Matrix Multiplication
• Matrix Transposition
• Finding the Determinate of a Matrix
• Matrix Inversion

9. Matrix Addition
• Matrix must be the same size in order to add
• Matrix addition is commutative:
A + B = B + A

10. Multiplication of a Matrix by a Scalar
• To multiple a matrix by a scalar, multiply each
element by the scalar:
• We often use this fact to simplify the display of
matrices with very large (or very small) values:

11. Multiplication of Matrices
 To multiple two matrices together, the matrices
must have compatible sizes:
 This multiplication is possible only if the number
of columns in A is the same as the number of rows
in B
 The resultant matrix C will have the same number
of rows as A and the same number of columns
as B

12. Multiplication of Matrices
• Consider these matrices:
• Can we find this product?
Yes, 3 columns of A = 3 rows of B
• What will be the size of C?
2 X 2: 2 rows in A, 2 columns in B

13. Multiplication of Matrices
• Element ij of the product matrix is computed
by multiplying each element of row i of the
first matrix by the corresponding element of
column j of the second matrix, and summing
the results
• This is best illustrated by example

14. Example – Matrix Multiplication
 Find
 We know that matrix C will be 2 × 2
 Element c11 is found by multiplying terms of row 1
of A and column 1 of B:

15. Example – Matrix Multiplication
• Element c12 is found by multiplying terms of row 1
of A and column 2 of B:

16. Example – Matrix Multiplication
• Element c21 is found by multiplying terms of row
2 of A and column 1 of B:

17. Example – Matrix Multiplication
• Element c22 is found by multiplying terms of row 2
of A and column 2 of B:

18. Example – Matrix Multiplication
• Solution:

19. Matrix Multiplication
• In general, matrix multiplication is not
commutative:
AB ≠ BA

20. Transpose of a Matrix
• The transpose of a matrix by switching its row
and columns
• The transpose of a matrix is designated by a
superscript T:

21. Types of Matrices
1. Row Matrix : A matrix which has only one row and n
numbers of columns called “Row Matrix”.
Ex : - [ 3 4 6 7 8 ………………n]
2. Column Matrix : A Matrix which has only one column
and n numbers of rows called “column Matrix”.
3567....n

22. Types of Matrices
 Square Matrix : A matrix which has equal number
of rows and columns called “Square Matrix”.
Where m =n
i.e the number of rows and columns are equal

23. Types of Matrices
 Diagonal Matrix : Diagonal matrix is a matrix in
which all elements are zero except the diagonal
elements.
 Remark : Diagonal matrix is a type of square
matrix.

24. Types of Matrices
Scalar Matrix :
It is a type of square matrix but its
all diagonal elements are exactly similar and
remaining elements should be zero
Where m = n, i.e the number of rows and
columns are equal

25. Ty Tpyepse so fo fM Maattrriicceess
 Unit matrix :
A Diagonal matrix which has all its
diagonal elements as 1 called “Unit Matrix”
Remark : Except diagonal elements all elements
should be zero.

26. Types of Matrices
 Null Matrix :
A matrix whose all elements are zero called
“Null Matrix”.
Remark: This matrix is also type of square matrix.

27. Types of Matrices
 Symmetric Matrix :
A matrix which is equal to its transpose
said to be “Symmetric Matrix”
A =
We can see that A =AT

28. T yTpyepse os fo Mf Mataritcreicse s
 Skew - Symmetric Matrix :
A matrix which is equal to its
negative of its transpose said to be “Skew-
Symmetric Matrix”
A =
We can see that A = - AT

29.  Lower Triangular matrix :-
If all the elements below the diagonal are zero
then this type of matrix is called “Lower Triangular
matrix”
For Ex.
Types of Matrices

30. Types of Matrices
 Upper Triangular matrix :-
if all the elements above the diagonal are zero
then this type of matrix is called “Upper triangular
matrix”
For Ex.

31. Types of Matrices
 Identity Matrix (Unit Matrix):-
A matrix is said to be identity matrix if
all the diagonal elements are 1 and remaining
elements should be zero.

32. Types of Matrices
 Equal Matrices :-
Those matrices which has equal number
of rows as well column and all elements should be
same said to be “Equal Matrix”.
and are equal matrices

33. Types of Matrices
 Equivalence Matrix :-
Those matrices which has
equal number of rows as well column but not
all elements are same said to be “Equivalence
Matrix”.
and

34. Types of Matrices
Orthogonal matrix :-
An orthogonal matrix is one
whose transpose is also its inverse.
AT = A-1

35. Determinate of a Matrix
• The determinate of a square matrix is a scalar quantity
that has some uses in matrix algebra. Finding the
determinate of 2 × 2 and 3 × 3 matrices can be done
relatively easily:
• The determinate is designated as |A| or det(A) of 2 ×2:

36. Determinate of a Matrix
• 3 × 3:

37. Matrix Rank
 The rank of a matrix is simply the number of
independent row vectors in that matrix.
or
The number of non-zero rows in the matrix.
 The transpose of a matrix has the same rank as the
original matrix.
 To find the rank of a matrix by hand, use Gauss
elimination and the linearly dependant row vectors
will fall out, leaving only the linearly independent
vectors, the number of which is the rank.

38. Matrix inverse
 The inverse of the matrix A is denoted as A-1
 By definition, AA-1 = A-1A = I, where I is the identity
matrix.
 Theorem: The inverse of an nxn matrix A exists if and
only if the rank A = n.
 Gauss-Jordan elimination can be used to find the
inverse of a matrix by hand.

39. Inverse of a 2 x 2 matrix
Procedure
 There is a simple procedure to find the inverse of a two by
two matrix. This procedure only works for the 2 x 2
case.
 Find the inverse of
Δ= delta= difference of product of diagonal
elements

40. Inverse of a 2 x 2 matrix
Procedure
 Determine whether or not the inverse actually exists. We will
define
Δ =
As (2)2-1(3);
Δ is the difference of the product of the diagonal
elements of the matrix.
 In order for the inverse of a 2 x 2 matrix to exist, Δ
cannot equal to zero.
 If happens Δ to be zero, then we conclude the inverse does
not exist and we stop all calculations.
 In our case Δ = 1, so we can proceed.

41. Inverse of a 2 x 2 matrix
 Step 2. Reverse the entries of the main diagonal consisting
of the
two 2’s. In this case, no apparent change is noticed.
Step 3. Reverse the signs of the other diagonal entries 3
and 1 so they become -3 and -1

42. Inverse of a 2 x 2 matrix
Step 4. Divide each element of the matrix by Δ
which in this case is 1, so no apparent change will
be noticed.
 The inverse of the matrix is then
Remark: for verification AA-1 = I

43. Inverse of a 3 x 3 matrix
Procedure
We use a more general procedure to find the inverse of a 3 x 3
matrix.
1. Augment this matrix with the 3 x 3 identity matrix.
2. Use elementary row operations to transform the matrix on the
left side of the vertical line to the 3 x 3 identity matrix. The row
operation is used for the entire row so that the matrix on the
right hand side of the vertical line will also change.
3. When the matrix on the left is transformed to the 3 x 3 identity
matrix, the matrix on the right of the vertical line is the
inverse.

44. ProcInevdeurrsee of a 3 x 3 matrix
Procedure
Here are the necessary row operations:
 Step 1: Get zeros below the 1 in the first column by multiplying
row 1 by -2 and adding the result to R2. Row 2 is replaced by
this sum.
 Step2. Multiply R1 by 2, add result to R3 and replace R3 by that
result.
 Step 3. Multiply row 2 by (1/3) to get a 1 in the second row
first position.

45. Inverse of a 3 x 3 matrix
Continuation of Procedure
 Step 4. Add R1 to R2 and replace R1 by that sum.
 Step 5. Multiply R2 by 4, add result to R3 and replace R3 by that
sum.
 Step 6. Multiply R3 by 3/5 to get a 1 in the third row, third
position.

46. Inverse of a 3 x 3 matrix
Final result
 Step 7. Eliminate the 5/3 in the first row third position by
multiplying row 3 by -5/3 and adding result to Row 1.
 Step 8. Eliminate the -4/3 in the second row, third position by
multiplying R3 by 4/3 and adding result to R2.
 Step 9. You now have the identity matrix on the left, which is
our goal.

47. Normal form of a matrix
Where is the unit matrix of order r. hence ρ(A) = r

48. Square Matrices P & Q of Orders m & n
respectively , such that PAQ is in the normal
form
Working rule:-
1. write A = I A I
2. Reduce the matrix on L.H.S.to normal form by applying
elementary row or column operation.
Remark :
* if row operation is applied on L.H.S. then this operation is
applied on pre-factor of A on R.H.S
* if column operation is applied on L.H.S. then this operation
is applied on post-factor of A on R.H.S
 The matrices P and Q are not unique

49. Consistent and Inconsistent Systems of
Equations
 All the systems of equations that we have seen in this
section so far have had unique solutions. These are
referred to as Consistent Systems of Equations, meaning
that for a given system, there exists one solution set for
the different variables in the system or infinitely many sets
of solution. In other words, as long as we can find a
solution for the system of equations, we refer to that
system as being consistent
 Inconsistent systems arise when the lines or planes
formed from the systems of equations don't meet at any
point.

50. Consistency Chart

51. Eigen values and Eigen
vectors
Origin of Eigen values and Eigen vectors
 Eigen values and eigenvectors have their origins
in physics, in particular in problems where
motion is involved, although their uses extend
from solutions to stress and strain problems to
differential equations and quantum mechanics.
we can use matrices to deform a body - the
concept of STRAIN. Eigenvectors are vectors that
point in directions where there is no rotation.
Eigen values are the change in length of the
eigenvector from the original length.

52. Eigen values and Eigen vectors
 Let A be an nxn matrix and consider the vector
equation:
Ax = lx
 A value of l for which this equation has a solution x≠0
is called an Eigen value of the matrix A.
 The corresponding solutions x are called the Eigen
vectors of the matrix A.

53. Solving for Eigen Values
Ax=lx
Ax - lx = 0
(A- lI)x = 0
 This is a homogeneous linear system, homogeneous
meaning that the RHS are all zeros.
 For such a system, a theorem states that a solution exists
given that det(A- lI)=0.
 The Eigen values are found by solving the above equation.

54. Solving for Eigen values cont’
 Simple example:
find the Eigen values for the matrix:
ù
úû
é
-
=
2 2
êë
5 2
-
A
 Eigen values are given by the equation det(A-lI) = 0:
- -
l
5 2
A l I
- =
l l l l
det( )
2 - 2
-
l
= - - - - - = 2+ +
( 5 )( 2 ) 4 7 6
 So, the roots of the last equation are -1 and -6.
These are the Eigen values of matrix A.

55. Eigenvectors
 For each Eigen value, l, there is a corresponding
eigenvector, x.
 This vector can be found by substituting one of the
Eigen values back into the original equation: Ax = lx
: for the example: -5x1 + 2x2 = lx1
2x1 – 2x2 = lx2
 Using l=-1, we get x2 = 2x1, and by arbitrarily
choosing x1 = 1, the Eigenvector corresponding to
l=-1 is:
2
é
-
x 1 and similarly,
úû
ù
úû
1
é
=
2
êë
ù
êë
=
1
2 x

56. Special matrices
 A matrix is called symmetric if:
AT = A
 A skew-symmetric matrix is one for which:
AT = -A
 An orthogonal matrix is one whose
transpose is also its inverse:
AT = A-1