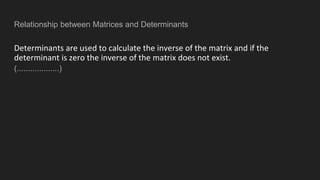
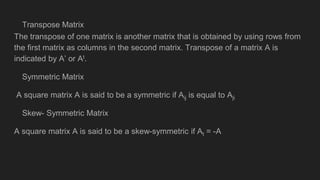
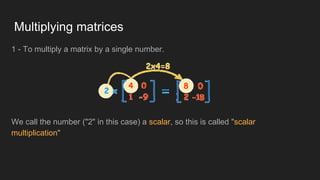
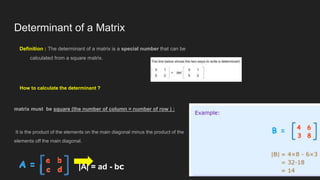
This document defines matrices and determinants, including examples and types of matrices. It describes how to add, subtract, and multiply matrices, and defines determinants and Cramer's rule. Cramer's rule is used to solve a 3x3 system of equations. The relationship between matrices and determinants is that determinants are uniquely related to square matrices but not vice versa, and determinants are used to calculate inverses.

1. MATRICES AND
DETERMINANTS

2. OBJECTIVES
Definition and examples of Matrices
Types of Matrices
Addition and Subtraction of Matrices
Multiplication and Division of Matrices
Definition and examples of Determinants
Cramer’s method for 2✕2 and 3✕3 systems (variables).
Relationship between Matrices and Determinants, with examples
Solution of the case using Cramer’s method

3. Matrices
A matrix is a rectangular arrangement of numbers into rows and columns.
The number of rows and columns that a matrix has is called its dimension or its
order. By convention, rows are listed first; and columns, second.
Numbers that appear in the rows and columns of a matrix are called elements of
the matrix.Two matrices are equal if all three of the following conditions are met:
 Each matrix has the same number of rows.
 Each matrix has the same number of columns.
 Corresponding elements within each matrix are equal.

4. Examples Of Matrices
Its dimensions are 2 ×3
2 rows and three columns
The entries of the matrix below are 2, -5,
10, -4, 19, 4.
The variable A in the matrix equation below represents
an entire matrix.

5. Types Of Matrices
Vectors
Vectors are a type of matrix having only one column or one row.
➔ Row vector or row matrix
➔ Column matrix or column vector
● Square Matrix
A matrix in which numbers of rows are equal to number of columns is called a
square matrix
Diagonal Matrix
A square matrix A is called a diagonal matrix if each of its non-diagonal element is
zero.

6. Transpose Matrix
The transpose of one matrix is another matrix that is obtained by using rows from
the first matrix as columns in the second matrix. Transpose of a matrix A is
indicated by A’ or At.
Symmetric Matrix
A square matrix A is said to be a symmetric if Aij is equal to Aji
Skew- Symmetric Matrix
A square matrix A is said to be a skew-symmetric if At = -A

7. Addition and Subtraction of Matrices
Two matrices may be added or subtracted only if they have the same dimension; that is, they must have
the same number of rows and columns.
Addition or subtraction is accomplished by adding or subtracting corresponding elements. For example,
consider matrix A and matrix B.
Both matrices have the same number of rows
and columns (2 rows and 3 columns), so they
can be added and subtracted. And finally, note
that the order in which matrices are added is
not important; thus, A + B = B + A.

8. Multiplying matrices
1 - To multiply a matrix by a single number.
We call the number ("2" in this case) a scalar, so this is called "scalar
multiplication"

9. 2 - Multiplying a Matrix by Another Matrix.
Step 1: Make sure that the the number of columns in the 1st one equals the
number of rows in the 2nd one. (The pre-requisite to be able to multiply)
Step 2: Multiply the elements of each row of the first matrix by the elements of
each column in the second matrix.

10. Exercise

11. Division of Matrices
We don’t actually divide the matrices we use the inverse of the matrix we write A-1
Let’s see this example:

12. Determinant of a Matrix
Definition : The determinant of a matrix is a special number that can be
calculated from a square matrix.
How to calculate the determinant ?
matrix must be square (the number of column = number of row ) :
It is the product of the elements on the main diagonal minus the product of the
elements off the main diagonal.
|A| = ad - bc

13. Cramer’s rule

16. Cramer’s Rule (3x3)

22. Solve the case
Solve the case by Cramer’s rule.

23. Step 1 : The case is in 3X3 format.We will write the values with variables x,y and
z.
ax + by + cz = j
dx + ey + fz = k
gx + hy + iz = l
Step 2 : In order to find x, y, z we will have to find determinant of A.
D = +3 ⎥ ⎥ -2 ⎥ ⎥ +1 ⎥ ⎥
D = 3 ( 2 - 2 ) -2 (2 - 6 ) +1 (1- 3 )
D = 3 (0) -2 (-4 ) +1 (-2 )
D = 0 + 8 -2 = 6
3 2 1
1 1 2
3 1 2
X
Y
Z
2.5
1.3
2.3
1 2
1 2
1 2
3 2
1 1
3 1

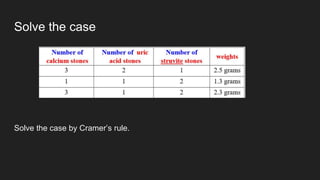
24. Step 3 : Find x by finding the determinant of x and dividing it by det of A.
= 2.5 ⎥ ⎥ -2 ⎥ ⎥ +1 ⎥ ⎥
Det of A
= [2.5 ( 2 - 2) - 2 ( 2.6 - 4.6) + 1 ( 1.3 - 2.3)]
6
=[0 - 4 - 1]
6
= -⅚
= -0.833
1 2
1 2
1.3 2
2.3 2
1.3 1
2.3 1

25. Relationship between Matrices and Determinants
● Matrices and Determinants are important concepts is Linear Algebra, where
matrices provide a concise way of representing large linear equations and
combination while determinants are uniquely related to a certain type of
matrices.

26. Relationship between Matrices and Determinants
● Matrices are categorized based on their special properties a matrix with an
equal number of rows and columns is known as a square matrix, and a
matrix with a single column is known as a vector.
● The determinant is a unique number associated with each square matrix.

27. Relationship between Matrices and Determinants
A determinant can be obtained from square matrices, but not the other way
around. A determinant cannot give a unique matrix associated with it.
The algebra concerning the matrices and determinants has similarities and
differences. Especially when performing multiplications. For example,
multiplication of matrices has to be done element wise, where
determinants are single numbers and follows simple multiplication.

28. Relationship between Matrices and Determinants
Determinants are used to calculate the inverse of the matrix and if the
determinant is zero the inverse of the matrix does not exist.
(...................)

30. Have A Nice Day