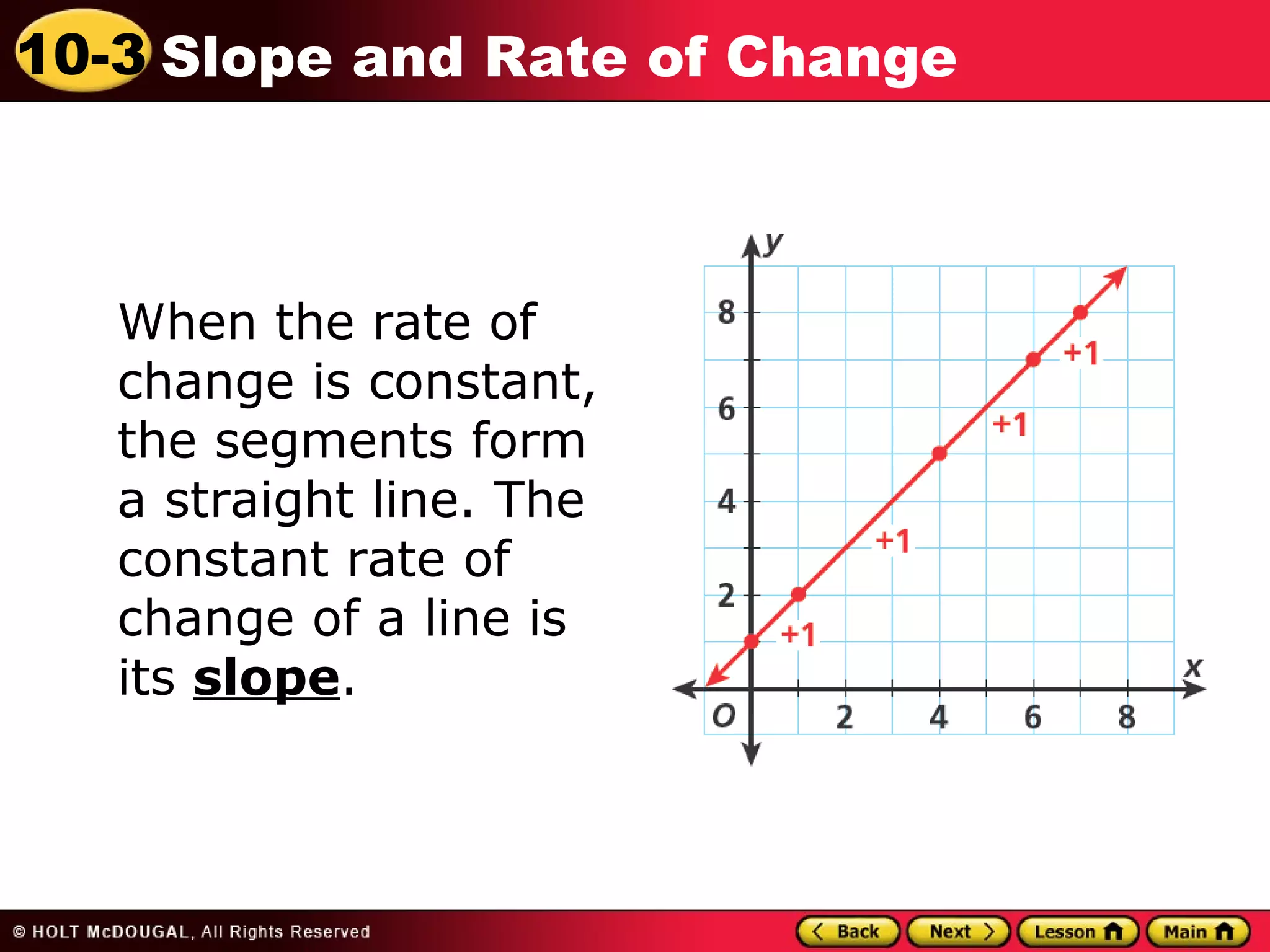
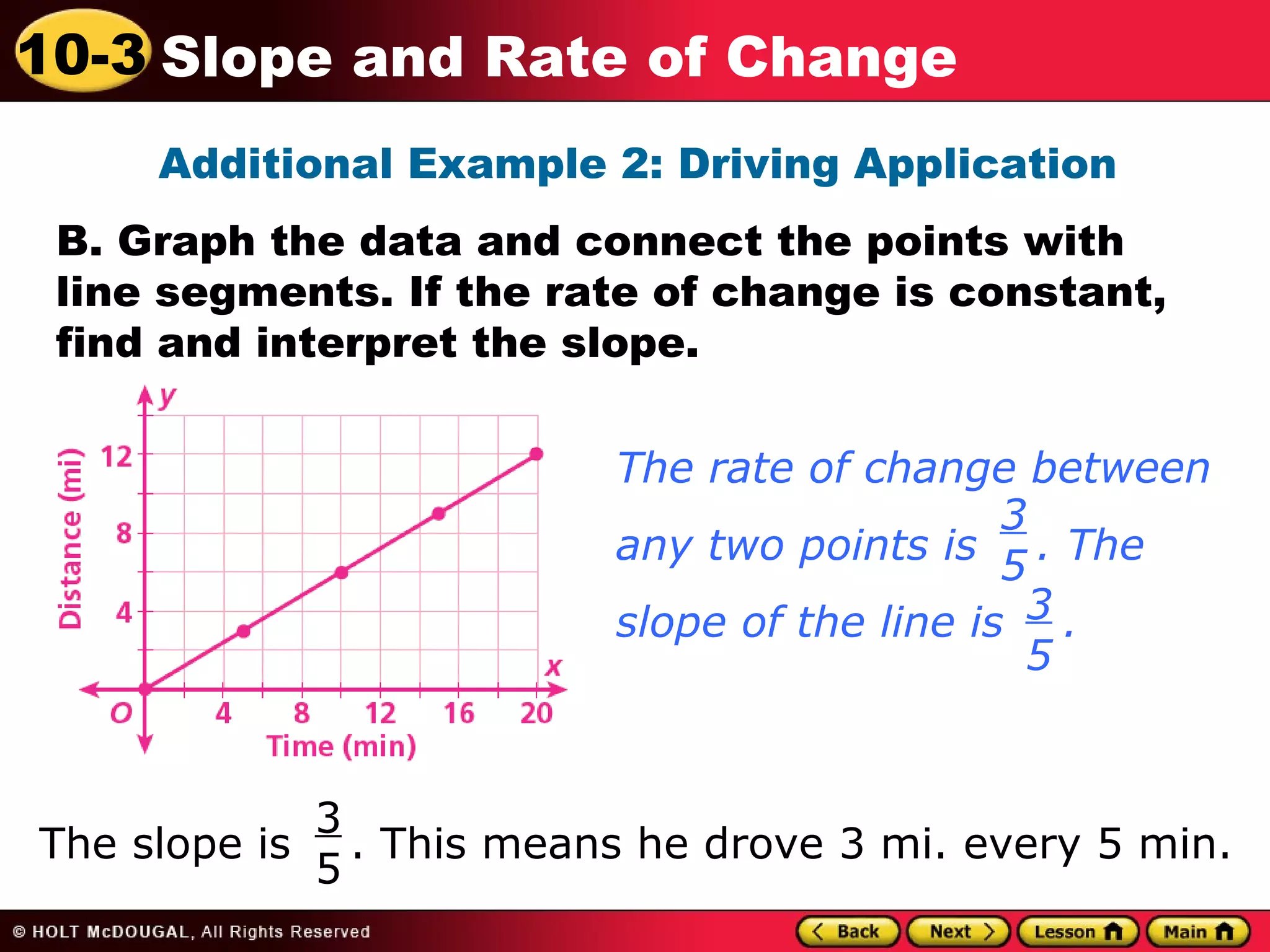
This document discusses slope and rate of change. It defines rate of change as a ratio that compares the difference in output values to the difference in input values. It provides examples of using tables of x-y data points to determine if the rates of change are constant or variable. When the rate of change is constant between data points, the graph will be a straight line, and the constant rate of change is defined as the slope.

1. 10-3 Slope and Rate of Change
Learn to find rates of change and slopes.

2. 10-3 Slope and Rate of Change
Vocabulary
rate of change
slope

3. 10-3 Slope and Rate of Change
The rate of change of a function is a
ratios that compares the difference
between two output values to the
difference between the corresponding
input values.

4. 10-3 Slope and Rate of Change
Additional Example 1A: Using A Table to identify
Rates of Change
Tell whether the rates of change are constant or
variable.
Find the
difference
between
consecutive data
points.
+2 +3 +1 +2
x 2 4 7 8 10
y 5 11 20 23 29
+6 +9 +3 +6
Find each ratio of the
change in y to the
change in x.
The rate of change is constant.

5. 10-3 Slope and Rate of Change
Caution!
Be careful to put the difference in y-values
in the numerator and the differences in
x-values in the denominator when you
write a rate of change.

6. 10-3 Slope and Rate of Change
Additional Example 1B: Using A Table to identify
Rates of Change
Tell whether the rates of change are constant or
variable. Find the
difference
between
consecutive data
points.
+1 +1 +1 +1
x 0 1 2 3 4
y 0 3 5 8 10
+3 +1 +3 +2
Find each ratio of the
change in y to the
change in x.
The rates of change are variable.

7. 10-3 Slope and Rate of Change
Check It Out: Example 1
Tell whether the rates of change are constant or
variable.
Find the
difference
between
consecutive data
points.
+2 +3 +1 +3
x 0 2 5 6 9
y 5 15 30 35 50
+10 +15 +5 +15
Find each ratio of the
change in y to the
change in x.
The rate of change is constant.

8. 10-3 Slope and Rate of Change
When the rate of
change is constant,
the segments form
a straight line. The
constant rate of
change of a line is
its slope.

9. 10-3 Slope and Rate of Change
Reading Math
Recall that a function whose graph is a
straight line is a linear function.

10. 10-3 Slope and Rate of Change
Additional Example 2: Driving Application
The table shows the driving distances that Jesse
recorded.
A. Determine whether the rates of change are
constant or variable.
The rate of change is constant.

11. 10-3 Slope and Rate of Change
Additional Example 2: Driving Application
B. Graph the data and connect the points with
line segments. If the rate of change is constant,
find and interpret the slope.
35
The rate of change between
any two points is . The
slope of the line is . 35
35
The slope is . This means he drove 3 mi. every 5 min.

12. 10-3 Slope and Rate of Change
Check It Out: Example 2
The table shows the driving distances that Barry
recorded.
Time (min) 1 3 6 9 12
Distance
3 6 12 18 24
(miles)
Determine whether the rates of change are
constant or variable.
31
= 3 63
= 2 12
6
= 2 18
9
The rates of change are variable.
= 2
24
12
= 2