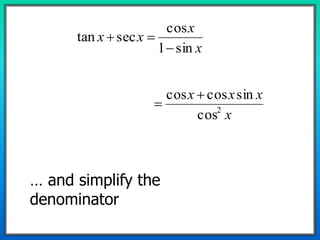
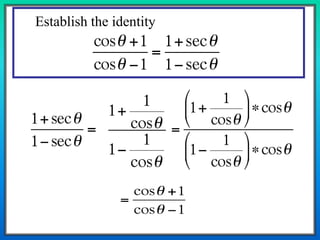
The document provides guidance on proving trigonometric identities by: 1) Working with one side of the identity at a time using algebraic manipulations and basic trigonometric identities until both sides are equal. 2) Examples are presented showing the step-by-step work for proving several identities including using quotient, reciprocal, and Pythagorean identities. 3) Tips are given for practicing proving identities including redoing examples without looking at the solutions and not getting discouraged if it takes multiple attempts.

1. www.PinoyBIX.org
Presents:
Proving Trigonometric Identities

2. Quick Review:



22
22
22
csc1cot
sectan1
1cossin



Quotient Identities
Reciprocal Identities Pythagorean Identities

3. We Verify (or Prove) Identities by
doing the following:
Work with one side at a time.
We want both sides to be exactly the
same.
Start with either side
Use algebraic manipulations and/or the
basic trigonometric identities until you
have the same expression as on the other
side.

4. Change everything on both sides to
sine and cosine.
Suggestions
 Start with the more complicated side
 Try substituting basic identities (changing all functions to
be in terms of sine and cosine may make things easier)
 Try algebra: factor, multiply, add, simplify, split up
fractions
 If you’re really stuck make sure to:

5. Remember to:
Work with only one side at a time!
x
x
x
xx
cot
sin
1
cos
csccosRHS




6.    xxxxxx 2
sincostancoscotsin 
Let’s start by working on
the left side of the
equation….

7.    xxxxxx 2
sincostancoscotsin 
  












x
x
x
x
x
x
cos
sin
cos
sin
cos
sin
Rewrite the terms inside
the second parenthesis
by using the quotient
identities

8.    xxxxxx 2
sincostancoscotsin 
  












x
x
x
x
x
x
cos
sin
cos
sin
cos
sin
Simplify

9.    xxxxxx 2
sincostancoscotsin 
  


















x
xx
x
x
x
sin
sin
1
sin
sin
cos
sin
To add the fractions
inside the
parenthesis, you must
multiply by one to get
common
denominators

10.    xxxxxx 2
sincostancoscotsin 
  






x
x
x
x
x
sin
sin
sin
cos
sin
2
Now that you have
the common
denominators, add
the numerators

11.    xxxxxx 2
sincostancoscotsin 
  




 
x
xx
x
sin
sincos
sin
2
Simplify

12.    xxxxxx 2
sincostancoscotsin 
xxxx 22
sincossincos 
Since the left side of the equation is
the same as the right side, you’ve
successfully proven the identity!

13. On to the
next problem….

14. xxxx 2244
sincossincos 
Let’s start by working on
the left side of the
equation….

15. xxxx 2244
sincossincos 
   xxxx 2222
sincossincos
We’ll factor the terms
using the difference of
two perfect squares
technique

16. xxxx 2244
sincossincos 
   1sincos 22
xx
Using the Pythagorean
Identities the second set
of parenthesis can be
simplified

17. xxxx 2244
sincossincos 
xxxx 2222
sincossincos 
Since the left side of the equation is
the same as the right side, you’ve
successfully proven the identity!

18. On to the
next problem….

19. x
x
xx
sin1
cos
sectan


Let’s start by working on
the right side of the
equation….

20. x
x
xx
sin1
cos
sectan












x
x
x
x
sin1
sin1
sin1
cos
Multiply by 1 in the form
of the conjugate of the
denominator

21. x
x
xx
sin1
cos
sectan


x
xx
2
sin1
)sin1(cos



Now, let’s distribute in
the numerator….

22. x
x
xx
sin1
cos
sectan


x
xxx
2
cos
sincoscos 

… and simplify the
denominator

23. x
x
xx
sin1
cos
sectan


x
xx
x
x
22
cos
sincos
cos
cos

‘Split’ the fraction and
simplify

24. x
x
xx
sin1
cos
sectan


x
x
x cos
sin
cos
1

Use the Quotient and
Reciprocal Identities to
rewrite the fractions

25. x
x
xx
sin1
cos
sectan


xx tansec 
And then by using the
commutative property of
addition…

26. x
x
xx
sin1
cos
sectan


xxxx sectansectan 
… you’ve successfully
proven the identity!

27. One more….

28. x
xx
2
csc2
cos1
1
cos1
1




Let’s work on the left
side of the equation…

29. x
xx
2
csc2
cos1
1
cos1
1























x
x
xxx
x
cos1
cos1
cos1
1
cos1
1
cos1
cos1
Multiply each fraction by
one to get the LCD

30. x
xx
2
csc2
cos1
1
cos1
1










x
x
x
x
22
cos1
cos1
cos1
cos1
Now that the fractions
have a common
denominator, you can
add the numerators

31. x
xx
2
csc2
cos1
1
cos1
1







x
xx
2
cos1
cos1cos1
Simplify the numerator

32. x
xx
2
csc2
cos1
1
cos1
1





 x2
cos1
2
Use the Pythagorean
Identity to rewrite the
denominator

33. x
xx
2
csc2
cos1
1
cos1
1





x2
sin
1
2
Multiply the fraction by
the constant

34. x
xx
2
csc2
cos1
1
cos1
1




xx 22
csc2csc2 
Use the Reciprocal Identity to
rewrite the fraction to equal
the expression on the right
side of the equation

35. How to get proficient at verifying
identities:
Once you have solved an identity go back
to it, redo the verification without looking at
how you did it before, this will make you
more comfortable with the steps you
should take.
Redo the examples done in class using
the same approach, this will help you build
confidence in your instincts!

36. Don’t Get Discouraged!
Every identity is different
Keep trying different approaches
The more you practice, the easier it will be
to figure out efficient techniques
If a solution eludes you at first, sleep on it!
Try again the next day. Don’t give up!
You will succeed!

37. Establish the identity

38. Establish the identity

39. Establish the identity

41. Homework
 TBA

42. Online Notes and Presentations
wwww.PinoyBIX.org
Visit:
credit: Kristen T and Jessica Garcia