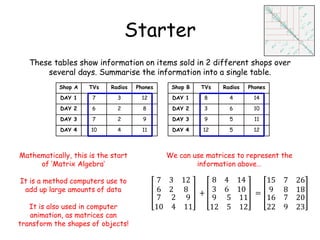
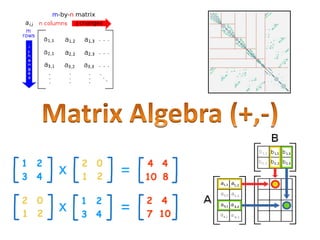
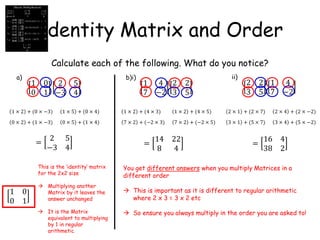
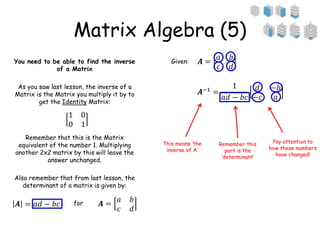
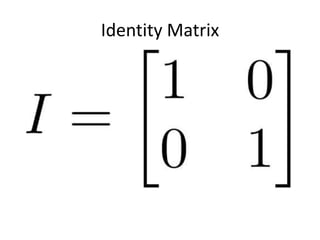This document provides information about further maths sessions and matrix algebra. It states that further maths sessions may cover topics students have not been taught or are already experts in, and provides past papers and questions for practice. It also provides instructions on using matrices to represent combined sales data from two shops and how to perform basic matrix operations like addition, subtraction, multiplication by a scalar and between matrices. These include using the correct matrix dimensions and order when performing operations.

2. Further Maths
• There are roughly 600,000 GCSE students in
the country at any one time
• Only 26,000 students sat AQA Further Maths
last year
• That means by just sitting the exam you are
potentially in the most able 4% of the country
• 93% of that 4% get a C or above

3. Further Maths
• What does that mean for you?
• There will be things in these sessions you may
not have been taught.
• They may be things that you are already
expert in.

4. Further Maths
• You will be given a set of past papers and a
booklet of questions.
• If you are already and expert on a topic you
can work on these questions (without
disturbing the session)
• Please bring the past papers to each session
(especially important on Friday)

5. Further Maths
• Remember Instagram and Twitter
• All of the resources and powerpoints will be
available through the blog.

6. Starter
These tables show information on items sold in 2 different shops over
several days. Summarise the information into a single table.
Mathematically, this is the start
of ‘Matrix Algebra’
It is a method computers use to
add up large amounts of data
It is also used in computer
animation, as matrices can
transform the shapes of objects!
Shop A TVs Radios Phones
DAY 1 7 3 12
DAY 2 6 2 8
DAY 3 7 2 9
DAY 4 10 4 11
Shop B TVs Radios Phones
DAY 1 8 4 14
DAY 2 3 6 10
DAY 3 9 5 11
DAY 4 12 5 12
7 3 12
6 2 8
7 2 9
10 4 11
+
8 4 14
3 6 10
9 5 11
12 5 12
=
15 7 26
9 8 18
16 7 20
22 9 23
We can use matrices to represent the
information above…

8. Matrix Algebra
To begin with, you need to know
how to solve problems involving
the addition and subtraction of
matrices, and be able to state
the ‘order’ of a matrix (its
dimensions)
The order of a matrix is (n x m)
where n is the number of rows
and m is the number of columns
Write the dimensions of the following matrices
2 −1
1 3
b)
1 0 2
d)4
−1
3 2
−1 1
0 −3
 2 rows
 2 columns
 The matrix
is 2 x 2
 1 row
 3 columns
 The matrix
is 1 x 3
 2 rows
 1 column
 The matrix
is 2 x 1
 3 rows
 2 columns
 The matrix
is 3 x 2

9. Matrix Algebra
To begin with, you need to know
how to solve problems involving
the addition and subtraction of
matrices, and be able to state
the ‘order’ of a matrix (its
dimensions)
You can add and subtract
matrices only when they have
the same dimensions
𝑨 =
5 7 4
−6 −2 3
𝑩 =
8 −2 0
−3 8 −1
Calculate A + B
5 7 4
−6 −2 3
+
8 −2 0
−3 8 −1
=
26−9
4513
Calculate A - B
5 7 4
−6 −2 3
−
8 −2 0
−3 8 −1
=
4−10−3
49−3

11. Matrix Algebra (2)
You need to be able to
multiply a matrix by a
number, as well as another
matrix
Calculate:
a) 2A
b) -3A
𝑨 =
5 2
−4 0
𝑨 =
5 2
−4 0
a)
2𝑨 =
10 4
−8 0
𝑨 =
5 2
−4 0
b)
−3𝑨 =
−15 −6
12 0
Just multiply
each part by 2
Just multiply
each part by -3
So to multiply a matrix by a number,
you just multiply each part in the
matrix separately

12. Matrix Algebra (2)
You need to be able to
multiply a matrix by a
number, as well as another
matrix
To multiply matrices
together, multiply each ROW
in the first, by each COLUMN
in the second (like in the
starter)
 Remember for each row
and column pair, you need to
sum the answers!
a) Calculate the following
2 5 3
4
6
1
 Multiply each number in the row with the
corresponding number in the column
2 × 4 + 5 × 6 + 3 × 1
= 41

13. The values of x and y in these pairs of Matrices are the same.
Calculate what x and y must be!
𝑥 𝑦 5
3
= 20
𝑦 −2 2
𝑥
= −24
5𝑥 + 3𝑦 = 20
2𝑦 − 2𝑥 = −24
10𝑥 + 6𝑦 = 40
10𝑦 − 10𝑥 = −120
16𝑦 = −80
𝑦 = −5
𝑥 = 7
As an
equation
As an
equation Multiply by 2
Multiply by 5
Add the two equations together
Divide by
16
Then find x
𝑥 𝑦 5
3
= 20 𝑦 −2 2
𝑥
= −24

15. Matrix Algebra (3)
Multiplying Matrices together
 When you have more difficult matrices, follow
these steps:
 Write the order of the matrices, and hence the
order of the answer.
 Take the first row of the first matrix, and
multiply it by the first column of the second (as
you have been doing up until now). Remember these
will be added together (write the sum out first…)
 Then continue using the first row and multiply by
the next column (if there is one). Write the
answer down next to the first (horizontally)
 Once you have used the first row with all the
columns, repeat the process but with the second
row, (if there is one!) writing these answers below
the first set
 Continue until you have used all the rows with all
the columns
 Then calculate each sum – it will already be set out
in the correct position!
 Lets see an example!
Calculate the following:
5 6
3
4
1
2
1 x 2 2 x 2 1 x 2
=
5 × 3 + (6 × 4) 5 × 1 + (6 × 2)
= 39 17

16. Matrix Algebra (3)
Multiplying Matrices together
 When you have more difficult matrices, follow
these steps:
 Write the order of the matrices, and hence the
order of the answer.
 Take the first row of the first matrix, and
multiply it by the first column of the second (as
you have been doing up until now). Remember these
will be added together (write the sum out first…)
 Then continue using the first row and multiply by
the next column (if there is one). Write the
answer down next to the first (horizontally)
 Once you have used the first row with all the
columns, repeat the process but with the second
row, (if there is one!) writing these answers below
the first set
 Continue until you have used all the rows with all
the columns
 Then calculate each sum – it will already be set out
in the correct position!
 Lets see an example!
Calculate the following:
1 3
−5 0
3 7
4 −1
2 x 2 2 x 2 2 x 2
=
1 × 3 + (3 × 4)
=
15 4
−15 −35
1 × 7 + (3 × −1)
−5 × 3 + (0 × 4) −5 × 7 + (0 × −1)

17. Practise

18. Answers

19. Practise

21. Extra if needed…

22. Identity Matrix and Order
Calculate each of the following. What do you notice?
1 0
0 1
2 5
−3 4
1 4
7 −2
2 2
3 5
1 4
7 −2
2 2
3 5
a) b)i) ii)
=
2 5
−3 4
1 0
0 1
This is the ‘identity’ matrix
for the 2x2 size
 Multiplying another
Matrix by it leaves the
answer unchanged
 It is the Matrix
equivalent to multiplying
by 1 in regular
arithmetic
=
14 22
8 4
=
16 4
38 2
You get different answers when you multiply Matrices in a
different order
 This is important as it is different to regular arithmetic
where 2 x 3 = 3 x 2 etc
 So ensure you always multiply in the order you are asked to!
1 × 2 + (0 × −3) 1 × 5 + (0 × 4)
0 × 2 + (1 × −3) 0 × 5 + (1 × 4)
1 × 2 + (4 × 3) 1 × 2 + (4 × 5)
7 × 2 + (−2 × 3) 7 × 2 + (−2 × 5)
2 × 1 + (2 × 7) 2 × 4 + (2 × −2)
3 × 1 + (5 × 7) 3 × 4 + (5 × −2)

23. Identity Matrix

24. Solving Matrix Problems

25. Solving Matrix problems

26. Solving Matrix problems

27. Matrix Algebra (5)
You need to be able to find the inverse
of a Matrix
As you saw last lesson, the inverse of a
Matrix is the Matrix you multiply it by to
get the Identity Matrix:
Remember that this is the Matrix
equivalent of the number 1. Multiplying
another 2x2 matrix by this will leave the
answer unchanged.
Also remember that from last lesson, the
determinant of a matrix is given by:
1 0
0 1
𝑨 =
𝑎 𝑏
𝑐 𝑑
𝑨 = 𝑎𝑑 − 𝑏𝑐 for
Given: 𝑨 =
𝑎 𝑏
𝑐 𝑑
𝑨−1
=
1
𝑎𝑑 − 𝑏𝑐
𝑑 −𝑏
−𝑐 𝑎
This means ‘the
inverse of A’
Remember this
part is the
‘determinant’
Pay attention to
how these numbers
have changed!

28. Matrix Algebra (5)
You need to be able to find the inverse
of a Matrix
Find the inverse of the matrix given below:
𝑨 =
𝑎 𝑏
𝑐 𝑑 𝑨−1
=
1
𝑎𝑑 − 𝑏𝑐
𝑑 −𝑏
−𝑐 𝑎
3 2
4 3
𝑨 =
3 2
4 3
𝑨−1 =
1
3 × 3 − 2 × 4
3 −2
−4 3
𝑨−1 =
1
1
3 −2
−4 3
3 −2
−4 3
𝑨−1
=
Replace
the
numbers
as above
Work out
the
fraction
…
… which in this
case you don’t
need to write!
𝑆𝑜:
3 2
4 3
3 −2
−4 3
=
1 0
0 1

29. Matrix Transformation
Complete the sheet

30. ExtraQuestions