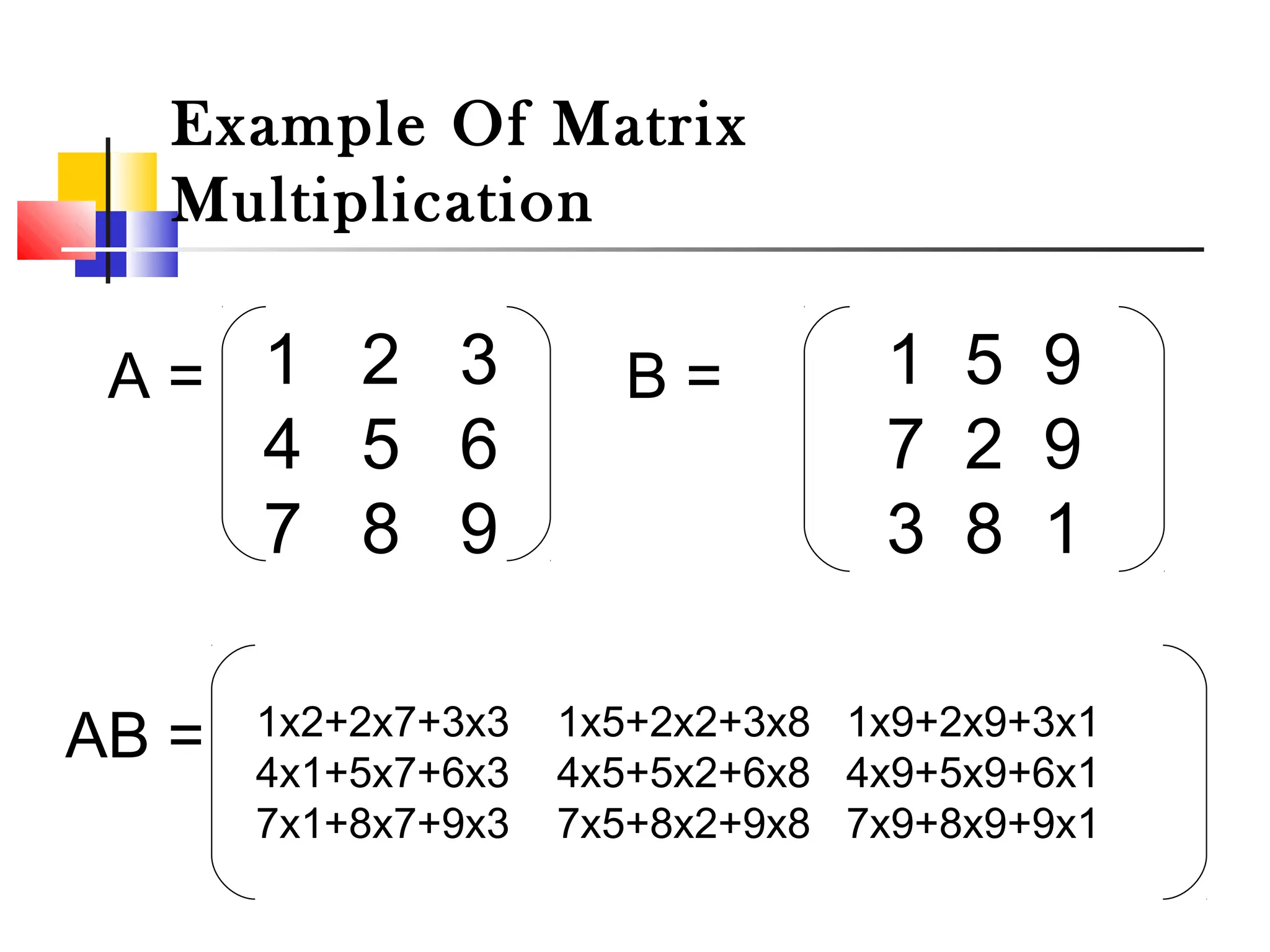
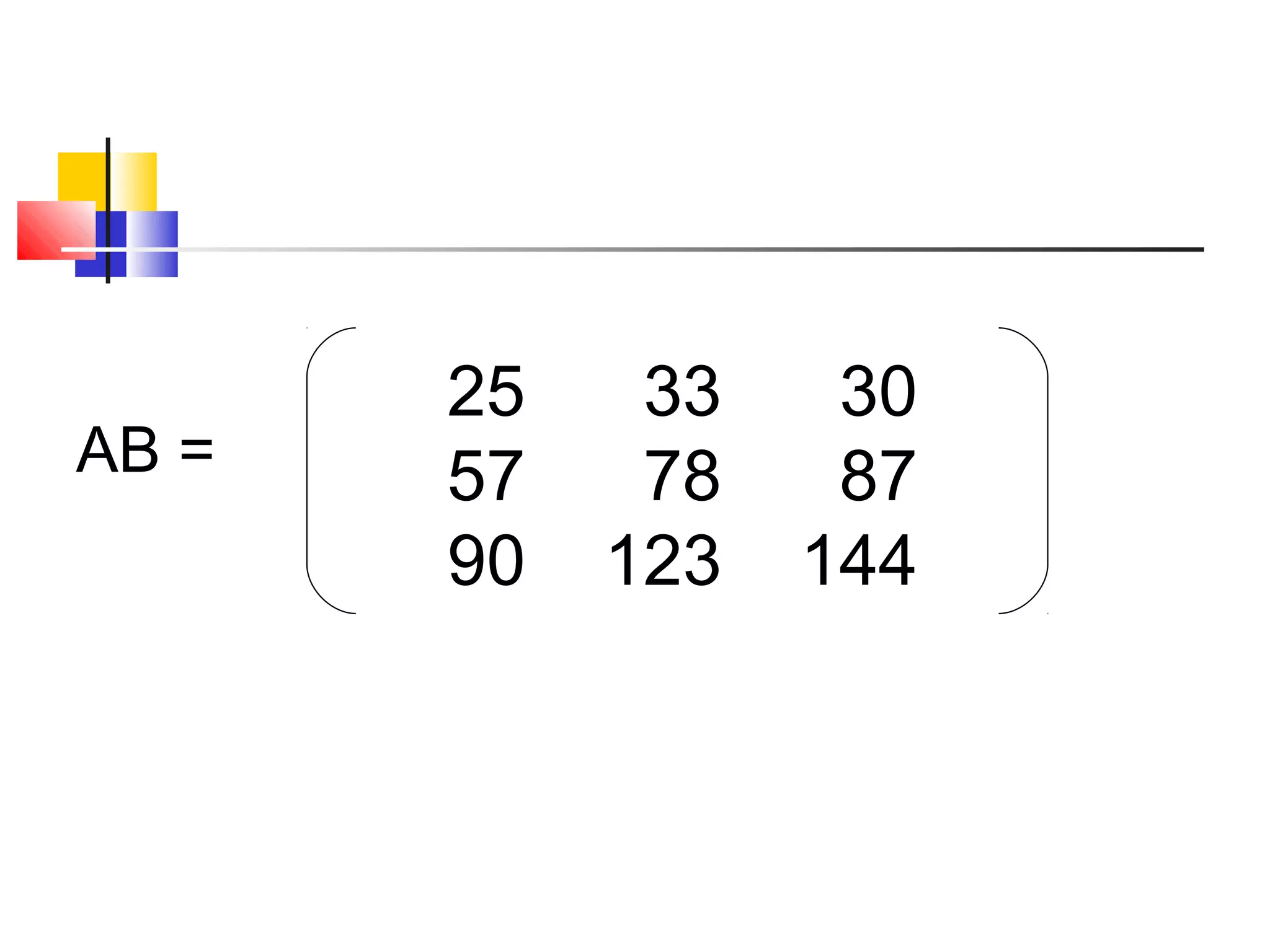
This document summarizes matrix operations including addition, subtraction, and multiplication. It defines a matrix as a rectangular arrangement of numbers in rows and columns. Matrix addition and subtraction can only be done on matrices with the same dimensions, by adding or subtracting the corresponding elements. Matrix multiplication involves multiplying the rows of the first matrix with the columns of the second matrix and summing the products to form the elements of the resulting matrix. Examples are provided to illustrate each operation.