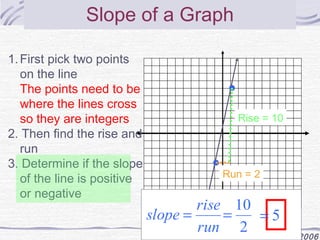
The document discusses slope and how to calculate it. It defines slope as the rate of change of a line and provides the formula slope=rise/run. It then explains how to find the slope of a line graph by picking two points and calculating rise over run. Finally, it demonstrates how to find the slope of a line given two points or from a table of x-y values using the same rise over run formula.

1. M. Pickens 2006
Slope

2. M. Pickens 2006
Objectives
• To learn what slope is
• To learn what a line looks like when it
has positive, negative, zero or undefined
slope
• To learn how to find the slope of a graph
• To learn how to find the slope given 2
points
• To learn how to find the slope of a table

3. = D (change in y)
M. Pickens 2006
What is Slope?
Slope is the rate of change of a line
slope = rise x
run
slope y
D
(change in x)
slope = y -
y
2 1
x -
x
2 1

4. What does the line look like when…
• You have positive slope?
• You have negative slope?
M. Pickens 2006
• You have zero slope?
• You have NO slope?

5. M. Pickens 2006
Slope
Mountain
Ski Resort
Positive
slope,
+ work
Negative
slope,
- work
Zero
slope is
zero fun!
NO
slope.
Oh No!!!!
T. Merrill 2005

6. M. Pickens 2006
Lets Cheer
Positive,
Negative
Zero
NO
X-Axis
Y-Axis
Go, Go, Go

7. What Type of Slope is
M. Pickens 2006
Shown?
Positive Slope
Negative Slope
Zero Slope
No
Slope/Undefined

8. M. Pickens 2006
Slope of a Graph
• When slope is positive or negative we
need to find the actual value of the
slope or rate of change
• On a graph we find slope using the
formula
slope = rise
run
How far up or down it changes
How far left or right it changes

9. = 2
M. Pickens 2006
Slope of a Graph
1.First pick two points
on the line
The points need to be
where the lines cross
so they are integers
2. Then find the rise and
run
3. Determine if the slope
of the line is positive
or negative
Rise = 2
Run = 3
slope = rise
run
3

10. = 10 = 5
M. Pickens 2006
Slope of a Graph
1.First pick two points
on the line
The points need to be
where the lines cross
so they are integers
2. Then find the rise and
run
3. Determine if the slope
of the line is positive
or negative
Rise = 10
Run = 2
slope = rise
run
2

11. Slope of a Graphed Line
RISE
1
- 4 = -
0 =
4
- 8 = -
3
2
M. Pickens 2006
Find the slope of each line below
Find the slope of each
line below
x
y
Slopes: =
RUN
1
4
4
4
0
6
1
2
4
= undefined
0

12. Slope of line through 2 points
• To find the slope of a line through 2
given points we use the formula
slope = y -
y
2 1
x -
x
• For example, Find the slope of a line
that goes through (--3, 3 5) 5 and (2, 2 18)
18
M. Pickens 2006
2 1
X1 y1 X2 y2
slope = y -
y
2 1
x -
x
2 1
= 13
5

13. Given two points on a line, find the slope:
1. (9, 2), (8, -7)
= - =
9
-
- 3
M. Pickens 2006
2. (-4, 4), (-7, 2)
-
7 4
2 4
2 4
3. (5, -1), (9, -4)
y y
2 1
x 2 x
1
rise
run
-
- -
8 9
7 2
-
1
-
y -
y
-
2 1
x 2 x
1
=
- - -
= 2
=
=
2
- - -
9 5
4 1
-
= -
-
-
- +
3
7 4
=
- +
9 5
4 1
-
4
X1 y1 X2 y2
= 9
X1 y1 X2 y2
X1 y1 X2 y2
3

14. Given two points on a line, find the slope:
4. (5, 2), (1, 0)
= - =
2
-
1 3 Undefined, NO slope
= 1
2 2 0 =
0
M. Pickens 2006
5. (3, -3), (3, -1)
- - -
3 3
1 3
- +
6. (-4, -2), (4, -2)
y y
2 1
x 2 x
1
rise
run
-
-
1 5
0 2
-
4
-
y -
y
-
2 1
x 2 x
1
=
-
=
2
= =
- - -
4 4
2 2
- -
-
0
3 3
=
- +
4 +
4
8
X1 y1 X2 y2
2
X1 y1 X2 y2
X1 y1 X2 y2

15. = +
4 2
-
= 6 = 3
M. Pickens 2006
Slope of a Table
• In a table we can use the same formula. Pick
any two pairs in the table for coordinates
x y
-4 -17
1 -2
3 4
8 19
10 25
slope = y -
y
2 1
x -
x
2 1
Pick any two rows.
If it is linear it will be the same
no matter which two rows you pick
x1
x2
y1
slope = - -
y2 3 1
4 2
-
3 1
2

16. slope = y -
y
2 1
x -
x
= -
3 2
- - -
= -
3 2
- +
= 1
M. Pickens 2006
Slope of a Table
• Find the slope for each table below
x y
-3 4.25
-1 2.75
0 2
1 1.25
5 -1.75
x y
-8 2
-6 3
-3 4.5
-1 5.5
0 6
slope = y -
y
2 1
x -
x
2 1
= -
2.75 4.25
- - -
1 3
= -1.5
2
= -0.75
= - 3
4
2 1
6 8
6 8
2

17. slope = y -
y
2 1
x -
x
= - - -
8 8
- - -
= - +
8 8
- +
= 0 = 0
M. Pickens 2006
Slope of a Table
• Find the slope for each table below
x y
slope = y -
y
2 1
x y
-10 17
x -
x
2 1
-3 -8
-5 10
= 10 -
17
-1 -8
-1 4.4
- 5 - -
10
0 -8
5 -4
= -
1 -8
10 -11
4 -8
10 17
- +
5 10
= - 7
5
2 1
1 3
1 3
2

18. slope = y -
y
2 1
x -
x
2 1
M. Pickens 2006
Conclusion
• Slope is:
the rate of change of a line
slope = rise
run
• Describe the slope of each of the following
Negative slope Undefined/
No slope
Positive slope Zero/0 slope