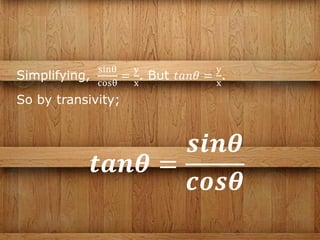
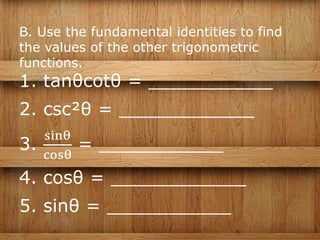
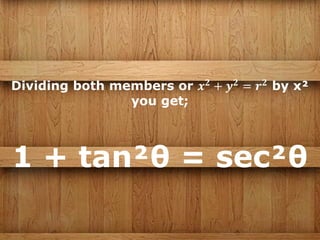The document discusses three main groups of trigonometric identities: reciprocal relations which relate trig functions that are inverse of each other like tangent and cotangent; quotient relations which show relationships between ratios of trig functions like tangent being equal to the sine over the cosine; and the Pythagorean relation which is the fundamental relationship between sine and cosine where the square of one added to the square of the other is equal to 1. Examples are provided for each type of identity and an activity is included to practice using and filling in identity formulas.

1. Trigonometric
Identities

2. Trigonometric Identity
Equalities that involve trigonometric
functions and are true for every single
value of the occurring variables.
 Identities involving certain functions of
one or more angles.

3. 3 Groups or Relation
Reciprocal Relation
Quotient Relation
Pythagorean Relation

4. Reciprocal Relation
The inverse trigonometric
functions are partial inverse
functions for the
trigonometric functions.

5. tan𝜃 =
y
x
and cot𝜃 =
x
y
therefore, tanθ and cotθ
are reciprocals of each other. The same thing
can be said about sinθ and cscθ as well as cosθ
and secθ.
𝒄𝒐𝒕𝜽 =
𝟏
𝒕𝒂𝒏𝜽
𝒔𝒆𝒄𝜽 =
𝟏
𝒄𝒐𝒔𝜽
𝒄𝒔𝒄𝜽 =
𝟏
𝒔𝒊𝒏𝜽

6. Since the product of a number and its
reciprocal equals 1, these relations may
also be written as:
tanθcotθ=1
cosθsecθ=1
sinθcscθ=1

7. Quotient
Relation

8. Simplifying,
sinθ
cosθ
=
y
x
. But 𝑡𝑎𝑛𝜃 =
y
x
.
So by transivity;
𝒕𝒂𝒏𝜽 =
𝒔𝒊𝒏𝜽
𝒄𝒐𝒔𝜽

9. Since cotθ is the reciprocal of tanθ the
quotient can be derived to get
𝒄𝒐𝒕𝜽 =
𝒄𝒐𝒔𝜽
𝒔𝒊𝒏𝜽

10. Pythagorean
Relation
 The basic relationship between the sine and
the cosine is the Pythagorean trigonometric
identity:
where cos2 θ means (cos(θ))2 and sin2 θ
means (sin(θ))2.
 This can be viewed as a version of
the Pythagorean theorem, and follows from
the equation x2 + y2 = 1for the unit circle.

11. By Pythagorean Theorem, 𝑥2
+ 𝑦2
=
𝑟2
. Dividing both members by r²
results to
x2
r2 +
y2
𝑟2 = 1. Since 𝑐𝑜𝑠𝜃 =
x
r
and 𝑠𝑖𝑛𝜃 =
y
r
, then,
cos²θ + sin²θ=1

12. Dividing both members or 𝒙 𝟐
+ 𝒚 𝟐
= 𝒓 𝟐
by x²
you get;
1 + tan²θ = sec²θ

13. dividing by y², you get;
cot²θ + 1 = csc²θ

14. Activity

15. A. Fill in the blanks to complete the table.
The Fundamental Trigonometric Identities and Their Alternate Forms
sinθcscθ = 1 1.
𝑠𝑖𝑛𝜃 =
1
cscθ
2.
𝑠𝑖𝑛𝜃 =
1
cosθ
𝑐𝑜𝑠𝜃 =
1
secθ
tanθcotθ = 1
𝑐𝑜𝑡𝜃 =
1
tanθ
3.
4.
𝑐𝑜𝑡𝜃 =
1
tanθ
5.
𝑐𝑜𝑡𝜃 =
sinθ
cosθ
6. 7.
sin²θ + cos²θ = 1 8. cos²θ = 1 - sin²θ
9. tan²θ = sec²θ - 1 sec²θ - tan²θ = 1
1 + cot²θ = csc²θ cot²θ = csc²θ - 1 10.

16. B. Use the fundamental identities to find
the values of the other trigonometric
functions.
1. tanθcotθ = ___________
2. csc²θ = ____________
3.
sinθ
cosθ
= ___________
4. cosθ = ____________
5. sinθ = ___________

17. Assignment
What are the terminologies
used in the graphs of
trigonometric function?
Define each.
Reference: Trigonometry
pages 141-142