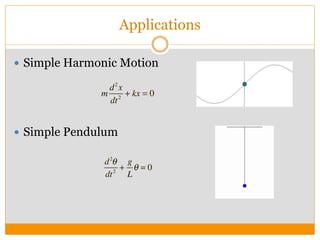
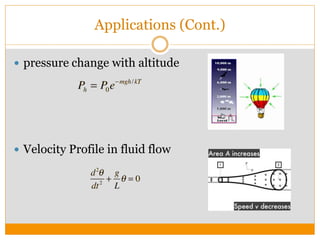
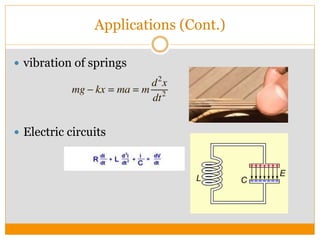
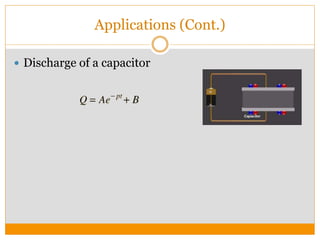
This document discusses higher order differential equations and their applications. It introduces second order homogeneous differential equations and their solutions based on the nature of the roots. Non-homogeneous differential equations are also discussed, along with their general solution being the sum of the solution to the homogeneous equation and a particular solution. Methods for solving non-homogeneous equations are presented, including undetermined coefficients and reduction of order. Applications to problems in various domains like physics, engineering, and circuits are also outlined.

1. Higher Order Differential Equation
&
Its Applications

2. Contents
 Introduction
 Second Order Homogeneous DE
 Differential Operators with constant coefficients
 Case I: Two real roots
 Case II: A real double root
 Case III: Complex conjugate roots
 Non Homogeneous Differential Equations
 General Solution
 Method of Undetermined Coefficients
 Reduction of Order
 Euler-Cauchy Equation
 Applications

3. Introduction
 A differential equation is an equation which contains
the derivatives of a variable, such as the equation
𝑎
𝑑2
𝑥
𝑑𝑡2
+ 𝑏
𝑑𝑥
𝑑𝑡
+ 𝑐𝑥 = 𝑑
Here x is the variable and a, b, c and d are constants.

4. Types of Differential Equations
 Homogeneous DE
 Non Homogeneous DE
0)()()()( 011
1
1  

 yxa
dx
dy
xa
dx
yd
xa
dx
yd
xa n
n
nn
n
n 
)()()()()( 011
1
1 xgyxa
dx
dy
xa
dx
yd
xa
dx
yd
xa n
n
nn
n
n  

 

5. Second Order Homogeneous DE
 A linear second order homogeneous differential
equation involves terms up to the second derivative
of a function. For the case of constant multipliers,
The equation is of the form
 and can be solved by the substitution

6. Solution
The solution which fits a specific physical situation is
obtained by substituting the solution into the equation and
evaluating the various constants by forcing the solution to
fit the physical boundary conditions of the problem at
hand. Substituting gives
which leads to a variety of solutions, depending on the
values of a and b. In physical problems, the boundary
conditions determine the values of a and b, and the
solution to the quadratic equation for λ reveals the nature
of the solution.

7. Case I: Two real roots
 For values of a and b such that
• there are two real roots m1 and m2 which lead to a general
solution of the form
21
1 2( ) nm x m xm x
ny x c e c e c e   K

8. Case II: A real double root
 If a and b are such that
 then there is a double root λ =-a/2 and the unique
form of the general solution is

9. Case III: Complex conjugate roots
 For values of a and b such that
 there are two complex conjugate roots of the form
and the general solution is

10.  The general solution of the non homogeneous
differential equation
There are two parts of the solution:
1. solution of the homogeneous part of DE
2. particular solution
( )ay by cy f x   
cy
py
Non Homogeneous
Differential Equations

11.  General Solution of non-homogeneous equation is
given by
 𝑦𝑐 represents solution of Homogeneous part
 𝑦𝑝 represents particular solution
c py y y 
General Solution

12. The method can be applied for the non – homogeneous differential
equations , if the f(x) is of the form:
• constant
• polynomial function
•
•
• A finite sum, product of two or more functions of type (1- 4)
( )ay by cy f x   
mx
e
sin ,cos , sin , cos ,...x x
x x e x e x 
   
Method of
Undetermined Coefficients

13. Reduction of Order
 We know the general solution of
is y = c1y1 + c2y1.
Suppose y1(x) denotes a known solution of (1). We assume the other
solution y2 has the form y2 = uy1.
Our goal is to find a u(x) and this method is called reduction of
order.


 dx
xy
e
xyy
dxxP
)(
)( 2
1
)(
12

14. Euler-Cauchy Equation
 Form of Cauchy-Euler Equation
 Method of Solution
We try y = xm, since
)(011
1
1
1 xgya
dx
dy
xa
dx
yd
xa
dx
yd
xa n
n
n
nn
n
n
n  


 
k
k
k
k
dx
yd
xa kmk
k xkmmmmxa 
 )1()2)(1( 
m
k xkmmmma )1()2)(1(  

15. Applications
 Simple Harmonic Motion
 Simple Pendulum

16. Applications (Cont.)
 pressure change with altitude
 Velocity Profile in fluid flow

17. Applications (Cont.)
 vibration of springs
 Electric circuits

18. Applications (Cont.)
 Discharge of a capacitor

19. References
 http://hyperphysics.phy-astr.gsu.edu/hbase/diff2.html#c2
 http://tutorial.math.lamar.edu/Classes/DE/IntroHigherOrder.aspx
 http://hyperphysics.phy-astr.gsu.edu/hbase/diff.html
 https://www.math.ksu.edu/~blanki/SecondOrderODE.pdf
 http://www.mylespaul.com/forums/showthread.php?t=266222

20. THANK YOU