The document discusses the Z-transform, which is a tool for analyzing and solving linear time-invariant difference equations. It defines the Z-transform, provides examples of common sequences and their corresponding Z-transforms, and discusses properties such as the region of convergence. Key topics covered include the difference between difference and differential equations, properties of linear time-invariant systems, and mapping between the s-plane and z-plane.

1. ‫ر‬َ‫ـد‬ْ‫ق‬‫ِـ‬‫ن‬،،،‫لما‬‫اننا‬ ‫نصدق‬ْْ‫ق‬ِ‫ن‬‫ر‬َ‫د‬
LECTURE (2)
The Z-Transform
ASCO. Prof. Amr E. Mohamed

2. Agenda
 Difference Equation vs Differential Equati
 Z-Transform
 Examples
 Properties
 Inverse Z-Transform
 Long Division
 Partial Fraction
 Solution of Difference Equation
 Mapping between s-plane to z-plane
2

3. Difference Equation vs Differential Equation
 A difference equation expresses the change in some variable as a result
of a finite change in the other variable.
 A differential equation expresses the change in some variable as a result
of an infinitesimal change in the other variable.
3

4. Differential Equation
 Following figure shows a mass-spring-damper-system. Where y is
position, F is applied force D is damping constant and K is spring
constant.
 Rearranging above equation in following form
4
𝐹 𝑡 = 𝑚 𝑦 𝑡 + 𝐷 𝑦 𝑡 + 𝐾𝑦(𝑡)
𝑦 𝑡 =
1
𝑚
𝐹 𝑡 −
𝐷
𝑚
𝑦 𝑡
𝐾
𝑚
𝑦(𝑡)

5. Differential Equation
 Rearranging above equation in following form
5
𝑦 𝑡 =
1
𝑚
𝐹 𝑡 −
𝐷
𝑚
𝑦 𝑡 −
𝐾
𝑚
𝑦(𝑡)
𝒅𝒕 𝒅𝒕𝟏
𝒎
−
𝑫
𝒎
−
𝑲
𝒎
𝑦 𝑦 𝑦𝐹(𝑡)


6. Difference Equation
6
𝑦 𝑘 + 2 =
1
𝑚
𝐹 𝑘 −
𝐷
𝑚
𝑦 𝑘 + 1 −
𝐾
𝑚
𝑦(𝑘)
𝟏
𝒛
𝟏
𝒛
𝟏
𝒎
−
𝑫
𝒎
−
𝑲
𝒎
𝑦(𝑘 + 2) 𝑦(𝑘)𝐹(𝑘)

𝑦(𝑘 + 1)

7. Difference Equations
 Difference equations arise in problems where the time is assumed to
have a discrete set of possible values.
 Where coefficients 𝑎 𝑛−1, 𝑎 𝑛−2,… and 𝑏 𝑛, 𝑏 𝑛−1,… are constant.
 𝑢(𝑘) is forcing function
7
𝑦 𝑘 + 𝑛 + 𝑎 𝑛−1 𝑦 𝑘 + 𝑛 − 1 + ⋯ + 𝑎1 𝑦 𝑘 + 1 + 𝑎0 𝑦 𝑘
= 𝑏 𝑛 𝑢 𝑘 + 𝑛 + 𝑏 𝑛−1 𝑢 𝑘 + 𝑛 − 1 + ⋯ + 𝑏1 𝑢 𝑘 + 1 + 𝑏0 𝑢 𝑘

8. Difference Equations
 Example 1: For the given difference equation, determine the (a)
order of the equation. Is the equation (b) linear, (c) time
invariant, or (d) homogeneous?
𝒚 𝒌 + 𝟐 + 𝟎. 𝟖𝒚 𝒌 + 𝟏 + 𝟎. 𝟎𝟕𝒚 𝒌 = 𝒖 𝒌
 Solution:
a) The equation is second order.
b) All terms enter the equation linearly
c) All the terms if the equation have constant coefficients.
Therefore the equation is therefore LTI.
d) A forcing function appears in the equation, so it is
nonhomogeneous.
8

9. Z-Transform
 Difference equations can be solved using z-transforms which provide a
convenient approach for solving LTI equations.
 The z-transform is an important tool in the analysis and design of
discrete-time systems.
 It simplifies the solution of discrete-time problems by converting LTI
difference equations to algebraic equations and convolution to
multiplication.
 Thus, it plays a role similar to that served by Laplace transforms in
continuous-time problems.
9

10. Z-transform Definition
 Given the causal sequence {x(ktT)}, its z-transform is defined as
 The variable z−1 in the above equation can be regarded as a time delay
operator.
10
X 𝑧 = 𝑥 0 + 𝑥 𝑇 𝑧−1
+ 𝑥 2𝑇 𝑧−2
+ ⋯ + 𝑥 𝑘𝑇 𝑧−𝑘
𝑋 𝑧 =
𝑘=0
∞
𝑥 𝑘𝑇 𝑧−𝑘

11. Example
 Obtain the Z-transform of the sequence
 Solution:
11
x 𝑘𝑇 = {1, 1, 3, 2, 0, 4, 0, 0, 0, … }
X 𝑧 = 1 + 𝑧−1
+3 𝑧−2
+ 2 𝑧−3
+ 4𝑧−5

12. Laplace Transform and Z-Transform
 Given the sampled impulse train of a signal
𝑥∗ 𝑡 = 𝑥 0 𝛿 𝑡 + 𝑥 𝑇 𝛿 𝑡 − 𝑇 + ⋯ + 𝑥 𝑘𝑇 𝛿(𝑡 − 𝑘𝑇) + ⋯
𝑥∗
𝑡 =
𝑘=0
∞
𝑥 𝑘𝑇 𝛿 𝑡 − 𝑘𝑇
12

13. Laplace Transform and Z-Transform
𝑋∗
𝑆 = 𝑥 0 + 𝑥 𝑇 𝑒−𝑠𝑇
+ 𝑥 2𝑇 𝑒−𝑠2𝑇
+ ⋯ + 𝑥 𝑘𝑇 𝑒−𝑠𝑘𝑇
+ ⋯
𝑋∗ 𝑆 =
𝑘=0
∞
𝑥 𝑘𝑇 𝑒−𝑠𝑘𝑇 =
𝑘=0
∞
𝑥 𝑘𝑇 (𝑒 𝑠𝑇)−𝑘 → (1)
 The z-transform is
𝑋 𝑧 =
𝑘=0
∞
𝑥 𝑘𝑇 𝑧−𝑘
→ (2)
 Comparing (1) and (2) yields
𝑧 = 𝑒 𝑠𝑇 where 𝑇 is the sample period
13

14. A Note
 In general, given a transfer function in s-domain you cannot just replace
𝑠 by s =
𝑙𝑛𝑧
𝑇
(from 𝑧 = 𝑒 𝑠𝑇
) to get its z-domain transfer function.
 The reason is that 𝑧 = 𝑒 𝑠𝑇 is true with the sampled signal.
14

15. Identities Used Repeatedly
𝑘=0
∞
𝑎 𝑘 =
1
1 − 𝑎
, 𝑎 < 1
𝑘=0
𝑛
𝑎 𝑘 =
1 − 𝑎 𝑛+1
1 − 𝑎
, 𝑎 = 1
 Special Cases:
𝑘=0
∞
𝑘𝑎 𝑘 =
1
(1 − 𝑎)2
, 𝑎 < 1
15

16. z-transform of the Unit impulse
 Let x(kT) = δ(kT)
 Then
16


 

otherwise0
0kfor1
(kT)
    1(kT)
00
 






k
k
k
k
zzkTxzX 

17. z-transform of the a Shifted Unit impulse
 Let x(kT) = δ(kT-qT)
 Then
17


 

otherwise0
qkfor1
qT)-(kT
  q
k
k
k
k
zzzkTxzX 






  00
qT)-(kT)( 

18. z-transform of a Unit-Step Function
 Let x(kT) = u(kT)
 Then
18


 

0kfor0
0kfor1
(kT)

u
 
11
1
(kT))( 1
000 


 









 z
z
z
zzuzkTxzX
k
k
k
k
k
k

19. z-transform of Sample Exponential
 Let x(kT) = ak u(kT)
 Then
19


 

0kfor0
0kfor
(kT)

k
k a
ua
  










000
(kT))(
k
kk
k
kk
k
k
zazuazkTxzX
 
az
z
az
azzX
k
k



 



 1
0
1
1
1
)(

20. z-transform of kaku[k]
 Let x(kT) = k ak u(kT)
 Then
20


 

0kfor0
0kfor
(kT)

k
k ka
uka
  










000
k(kT))(
k
kk
k
kk
k
k
zazukazkTxzX
  221
0
1
)()1(
1
)(k
az
z
az
azzX
k
k



 





21. z-transform of Sinusoids
 Let x(kT) = (cos ΩkT) u(kT)
 Then
 Similarly it can be shown:
21


 

0kfor0
0kfor)cos(
(n))cos(

kT
un
2
)k(cos
kTjkTj
ee
T



)}()({
2
1
u(k)})k({cos kTuekTueZT kTjkTj 








  TjTj
ez
z
ez
z
kTkT
2
1
)}u()({cos
1)(cos2
)(cos
)(cos21
)(cos1
)}u()({cos 2
2
21
1





 

Tzz
Tzz
zTz
Tz
kTkT
1)(cos2
)(s
)(cos21
)(s
)}u()({sin 221
1





 

Tzz
Tinz
zTz
Tinz
kTkT

22. 22
Signal, 𝐱(𝒌𝑻) Z-Transform, 𝐗(𝐳) Z-Transform, 𝐗(𝐳) ROC
1 𝛅(𝒌𝑻) 1 1 all Z
2 𝛅(𝒌𝑻 − 𝒒) 𝐳−𝒒 𝐳−𝒒 𝐳 ≠ 𝟎
3 𝐮(𝒌𝑻)
𝟏
𝟏 − 𝒛−𝟏
𝐳
𝐳 − 𝟏
𝐳 > 𝟏
4 𝐚 𝒌
𝐮(𝐤𝐓)
𝟏
𝟏 − 𝒂𝒛−𝟏
𝐳
𝐳 − 𝐚
𝐳 > 𝐚
5 𝒌 𝐮(𝐤𝐓)
𝟏
(𝟏 − 𝒛−𝟏) 𝟐
𝐳
(𝐳 − 𝟏) 𝟐
𝐳 > 𝟏
6 𝒌 𝐚 𝒌 𝐮(𝐤𝐓)
𝐚𝒛−𝟏
(𝟏 − 𝐚𝒛−𝟏) 𝟐
𝐚𝐳
(𝐳 − 𝐚) 𝟐
𝐳 > 𝐚
7 𝐜𝐨𝐬(𝛚 𝟎 𝐤𝐓)
𝟏 − 𝒛−𝟏
𝐜𝐨𝐬(𝛚 𝟎)
𝟏 − 𝟐𝒛−𝟏 𝐜𝐨𝐬 𝛚 𝟎 + 𝒛−𝟐
𝐳 𝟐
− 𝐳𝐜𝐨𝐬(𝛚 𝟎)
𝐳 𝟐 − 𝟐𝐳 𝐜𝐨𝐬 𝛚 𝟎 + 𝟏
𝐳 > 𝟏
8 𝐬𝐢𝐧(𝛚 𝟎 𝐤𝐓)
𝒛−𝟏
𝐬𝐢𝐧(𝛚 𝟎)
𝟏 − 𝟐𝒛−𝟏 𝐜𝐨𝐬 𝛚 𝟎 + 𝒛−𝟐
𝐳 𝐬𝐢𝐧(𝛚 𝟎)
𝐳 𝟐 − 𝟐𝐳 𝐜𝐨𝐬 𝛚 𝟎 + 𝟏
𝐳 > 𝟏
9 𝐫 𝒌
𝐜𝐨𝐬(𝛚 𝟎 𝐤𝐓)
𝟏 − 𝐫 𝒛−𝟏
𝐜𝐨𝐬(𝛚 𝟎)
𝟏 − 𝟐𝐫 𝒛−𝟏 𝐜𝐨𝐬 𝛚 𝟎 + 𝐫 𝟐 𝒛−𝟐
𝐳 𝟐
− 𝒓 𝐳 𝐜𝐨𝐬(𝛚 𝟎)
𝐳 𝟐 − 𝟐𝒓 𝐳 𝐜𝐨𝐬 𝛚 𝟎 + 𝐫 𝟐
𝐳 > 𝐫
10 𝐫 𝒌
𝐬𝐢𝐧(𝛚 𝟎 𝐤𝐓)
𝒓 𝒛−𝟏 𝐬𝐢𝐧(𝛚 𝟎)
𝟏 − 𝟐𝐫 𝒛−𝟏 𝐜𝐨𝐬 𝛚 𝟎 + 𝐫 𝟐 𝒛−𝟐
𝒓 𝐳 𝐬𝐢𝐧(𝛚 𝟎)
𝐳 𝟐 − 𝟐𝒓 𝐳 𝐜𝐨𝐬 𝛚 𝟎 + 𝐫 𝟐
𝐳 > 𝐫

23. Z-Transform Properties
23

24. 24
Z-Transform Properties: Linearity
 Notation
 Linearity
 Example:
   zXkTxzXkTx ZZ
2211 )(&)( 
   zXbzXakTxbkTxa Z
2121 )()( 
)(u3a-)(4)( k
kTkTukTx 
 
)1)(1(
)43(1
1
3
1
4
11
1
11 









azz
za
azz
zX

25. Z-Transform Properties: Time Right Shifting (Time Delay)
 Use the time delay property of the Laplace Transform
 Then
 Example:
25
 zXznTkTx nZ 
 )(
 SXeTtx TSZ
d

 )(
))3(()2.0()( )3(
TkukTx Tk
 
1
3
2.01
1
)( 



z
zZX

26. Z-Transform Properties: Time Left Shifting (Time Advance)
 Example:
26
  ])([)(
1
0





n
k
knZ
zkTxzXznTkTx
))2(()2.0()( )2(
TkukTx Tk
 
])(
2.01
1
[)(
1
0
1
2






k
k
zkTx
z
zZX
1
1
1
2
2.01
04.0
)]2.01(
2.01
1
[)( 






z
z
z
zZX

27. Z-Transform Properties: Multiplication by Exponential
27
 azXkTxa Zk
/)( 
 Example:

28. Z-Transform Properties: Complex Differentiation
28
 
dz
zdX
zkTxk Z
)(
 zX
dz
d
zkTxk
m
Zm






)(

29. Z-Transform Properties: Convolution
 Convolution in time domain is multiplication in z-domain
 Example: Let’s calculate the convolution of
 Multiplications of z-transforms is
29
       zXzXkTxkTx Z
2121 
       kTukTkTuakTx kT
 21 xand
     
  1121
11
1



zaz
zXzXzY
   zXkTxzXkTx ZZ
2211 )(&)( 

30. Z-Transform Properties: Initial and Final Value Theorems
 Initial Value Theorem:
 The value of x(n) as k → 0 is given by:
 Final Value Theorem:
 The value of x(n) as k →  is given by:
30
  )(limlim)0(
0
zXkTxx
zk 

  )]()1[(limlim)(
1
zXzkTxx
zk



31. The inverse Z-Transform
31

32. 32
The Inverse Z-Transform
 Formal inverse z-transform is based on a Cauchy integral
 Less formal ways sufficient most of the time
1) Direct or Long Division Method
2) Partial fraction expansion and Look-up Table
3) Inversion Integral Method (Residue-theorem)
       dzzzX
j
zXZkTx k
C
11
2
1 



33. 33
Inverse Z-Transform: Power Series Expansion
 Using Long Division to expand X(z) as a series
 Write the inverse transform as the sequence
         




0
21
...20
k
k
zkTxzTxzTxxzX
        ...},2,,0{ TxTxxkTx 

34. 34
Inverse Z-Transform: Power Series Expansion
 Example
    
321
111
2
1
2
1
1
11
2
1
1










zzz
zzzzX
         TkTTkTTkTkTkTx 3
2
1
2
2
1
 
 















Otherwise
k
k
k
k
kTx
0
3
2
1
21
1
2
1
01

35. Inverse Z-Transform: Power Series Expansion
 Example: Find x(n) for n = 0, 1, 2, 3, 4, when X(z) is given by:
 Solution:
 First, rewrite X(z) as a ratio of polynomial in 𝑧−1
, as follows:
 Dividing the numerator by the denominator, we have:
35
 
  2.01
510



zz
z
zX
  21
21
2.02.11
510





zz
zz
zX
4321
68.184.181710 
 zzzz
21
2.02.11 
 zz 21
510 
 zz
32
217 
 zz
432
4.34.2017 
 zzz
43
4.34.18 
 zz
543
68.308.224.18 
 zzz
54
68.368.18 
 zz
654
736.3416.2268.18 
 zzz
321
21210 
 zzz Therefore,
• x(0) = 0,
• x(1) = 10,
• x(2) = 17,
• x(3) = 18.4
• x(4) = 18.68

36. Inverse Z-Transform: Partial Fraction Expansion
 Assume that a given z-transform can be expressed as
 Apply partial fractional expansion
 First term exist only if M>N
 Br is obtained by long division
 Second term represents all first order poles
 Third term represents an order s pole
 There will be a similar term for every high-order pole
 Each term can be inverse transformed by inspection
36
 






 N
0k
k
k
M
0k
k
k
za
zb
zX
 
  










s
1m
m1
i
m
N
ik,1k
1
k
k
NM
0r
r
r
zd1
C
zd1
A
zBzX

37. Inverse Z-Transform: Partial Fraction Expansion
 Coefficients are given as
 Easier to understand with examples
37
 
  










s
m
m
i
m
N
ikk k
k
NM
r
r
r
zd
C
zd
A
zBzX
1
1
,1
1
0 11
    kdzkk zXzdA 

 1
1
   
     1
1
1
!
1















idw
s
ims
ms
ms
i
m wXwd
dw
d
dms
C

38. Example:
 Find x(kT) if X(z) is given by:
 Solution: We first expand X(z)/z into partial fractions as follows :
 Then we obtain
 then
38
 
  2.01
10


zz
z
zX
 
      2.0
5.12
1
5.12
2.01
10






zzzzz
zX
  









2.01
5.12
z
z
z
z
zX
  )()2.0(5.12)(5.12 kTukTukTx k

  )(11
kTZ 
 kTu
z
z
Z 







1
1
 kTua
az
z
Z n







1

39. Another Solution
 In this example, if X(z), rather than X(z)/z, is expanded into partial
fractions, then we obtain:
 However, by use of the shifting theorem we find :
 Then
39
 
   2.0
5.2
1
5.12
2.01
10






zzzz
z
zX
  








 
2.0
5.2
1
5.12 11
z
z
z
z
z
zzX
  )(2.015.12)()2.0(
2.0
5.2
)(5.12)(
)()2.0(5.2)(5.12)( 1
TkTuTkTuTkTukTx
TkTuTkTukTx
kk
k

 
 
 
 
 
 
..
..
48.124
4.123
122
101
00





x
x
x
x
x
     TnkTxzXzZ o
no
1

40. Example:
 Find x(kT) if X(z) is given by:
 Solution: Expand X(z)/z into partial fraction as follows:
 Then:
 By referring to tables we find that x(kT) is given by:
 and therefore,
 x(0) = 0 -1 +3 = 2
 x(1) = 18 – 2 + 3= 19
40
 
   12
2
2
3



zz
zz
zX
 
      1
3
2
1
2
9
12
12
22
2









zzzzz
z
z
zX
 
     1
3
22
9
2






z
z
z
z
z
z
zX
  )(3)()2()()2(5.4 kTukTukTrkTx kk

 kTuk
k
kk
kTr 


 

00
0
)(

 
 kTr
z
z
Z 







2
1
1
 
 kTra
az
az
Z k








2
1

41. Solution of Difference Equations
41

42. Transfer Function Representation
 First – Order Case
 Let 𝒚(𝒌𝑻) + 𝒂𝒚(𝒌𝑻 − 𝑻) = 𝒃𝒙(𝒌𝑻)
 Then take the z-transform to get:
• 𝒀(𝒛) + 𝒂 𝒛
− 𝟏 𝒀(𝒛) = 𝒃 𝑿(𝒛)
 Simplifying:
• 𝒀(𝒛) (𝟏 + 𝒂𝒛
− 𝟏) = 𝒃 𝑿(𝒛)
• 𝒀(𝒛) = (𝒃 𝑿(𝒛))/ (𝟏 + 𝒂𝒛
− 𝟏)
 And we have the transfer function H(z):
• 𝒀(𝒛) = 𝑯(𝒛) 𝑿(𝒛)
• so  𝑯(𝒛) =
𝒃 𝒛
𝒛 + 𝒂
 By inverse z-transform: 𝒚 𝒌𝑻 = 𝒃 −𝒂 𝒌
𝒖(𝒌𝑻) 42

43. Mapping between s-plane to z-plane
43

44. Mapping between s-plane to z-plane
 Where 𝑠 = 𝜎 + 𝑗𝜔 for real number 𝜎 and real number 𝜔.
 Then 𝑧 in polar coordinates is given by
44
𝑧 = 𝑒(𝜎+𝑗𝜔)𝑇
𝑧 = 𝑒 𝜎𝑇
𝑒 𝑗𝜔𝑇
∠𝑧 = 𝜔𝑇𝑧 = 𝑒 𝜎𝑇
𝑧 = 𝑒 𝑠𝑇

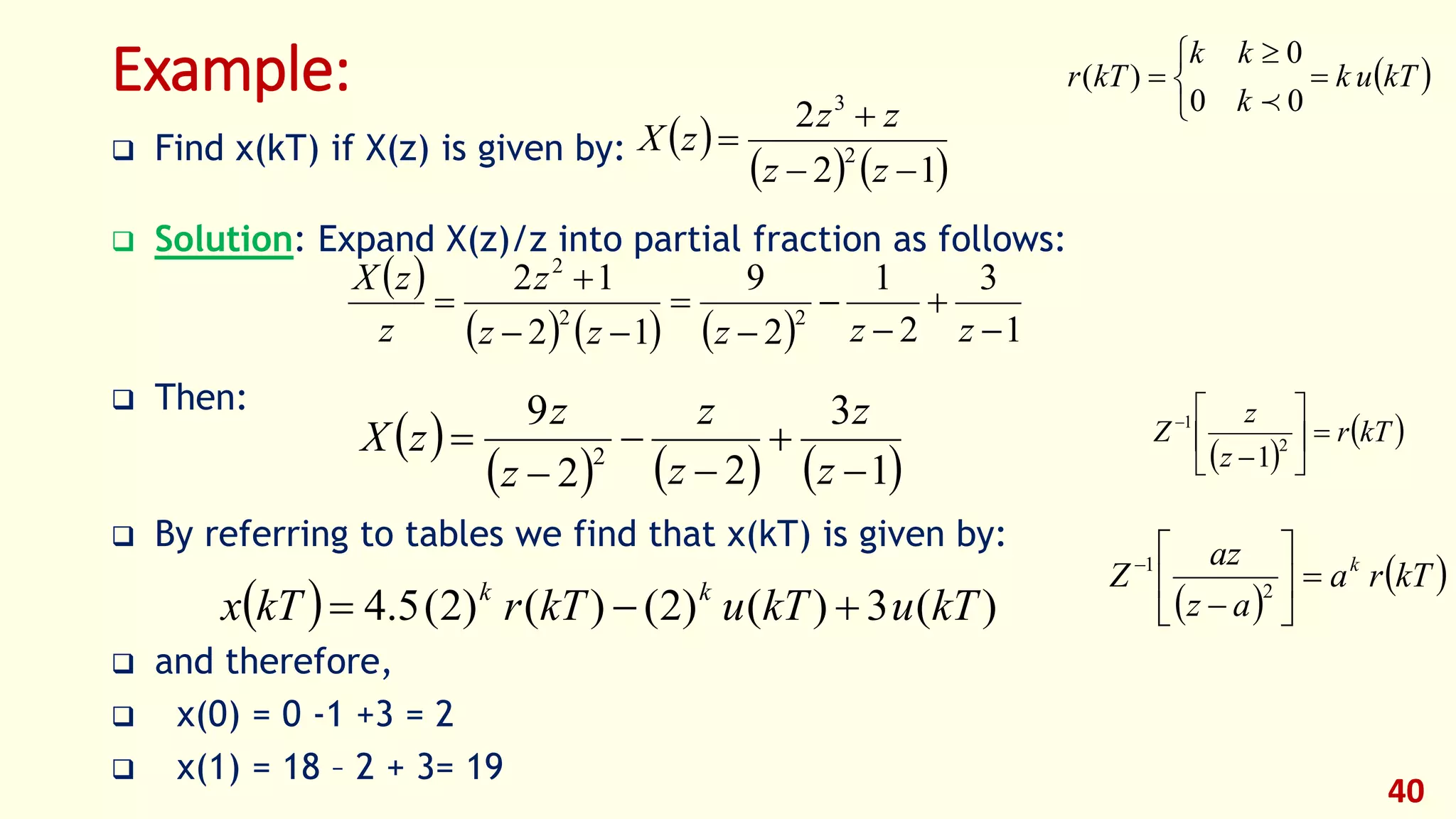
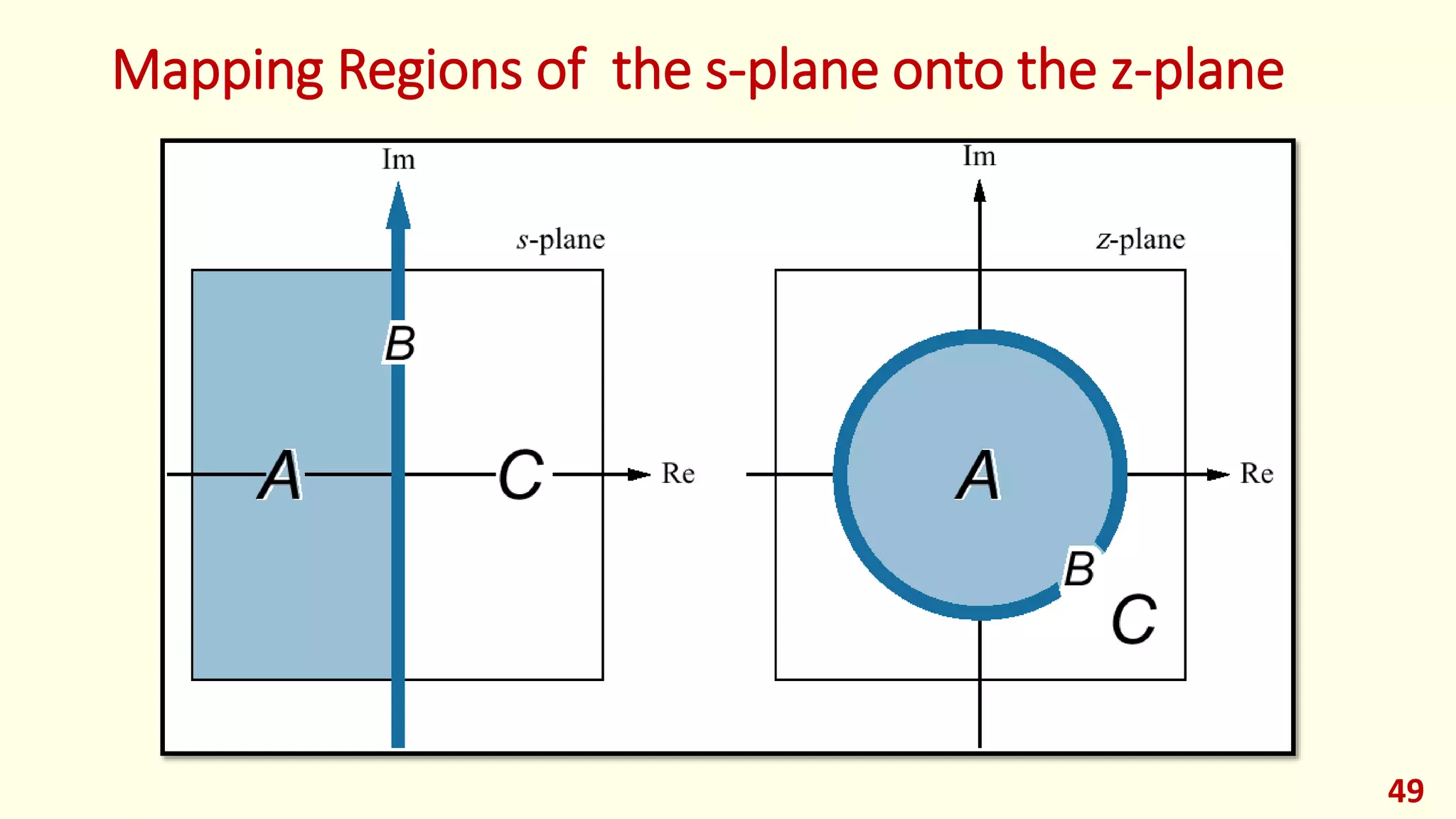
45. Mapping between s-plane to z-plane
 We will discuss following cases to map given points on s-plane to z-
plane.
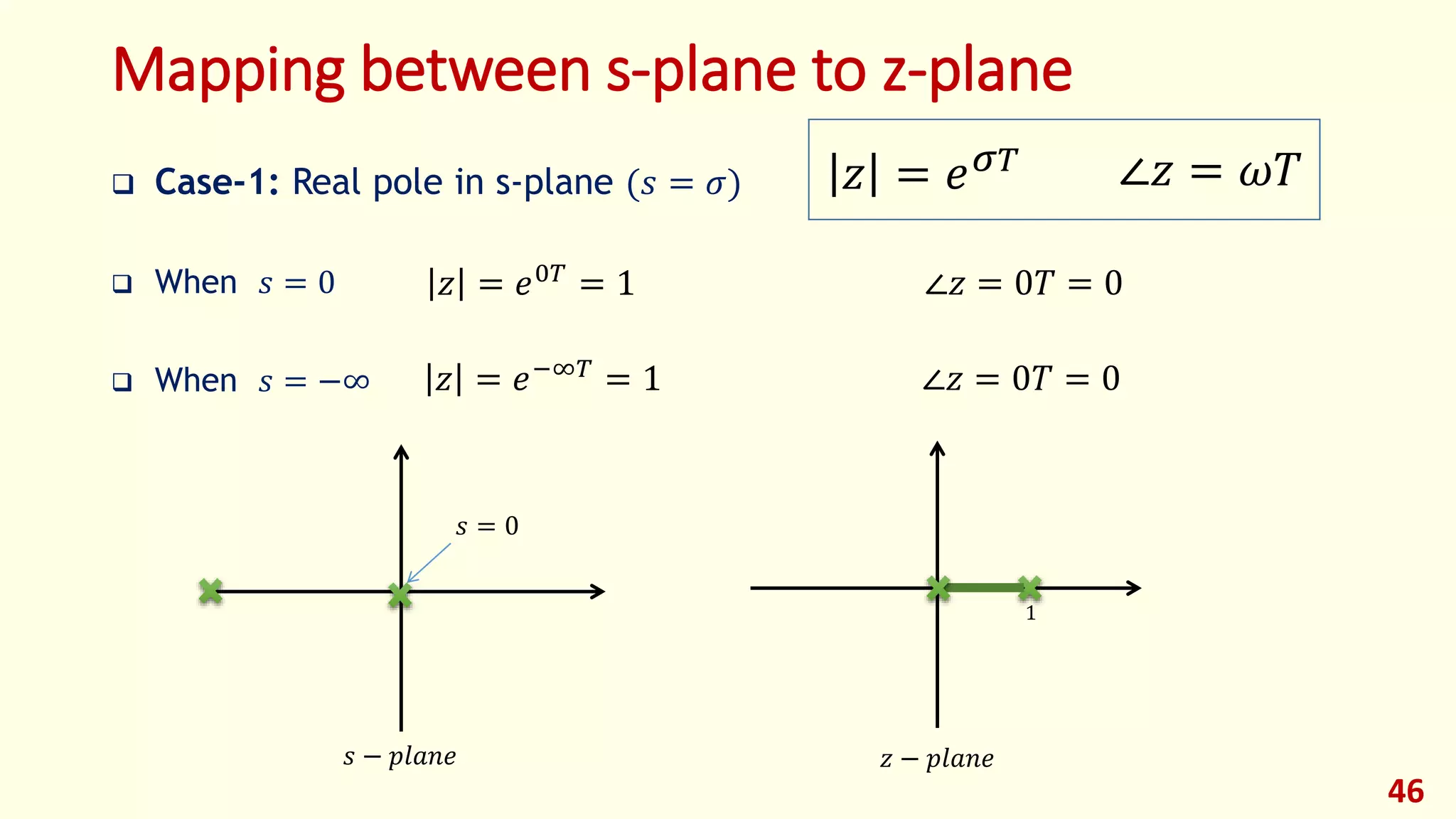
 Case-1: Real pole in s-plane (𝑠 = 𝜎) [on the left hand-side]
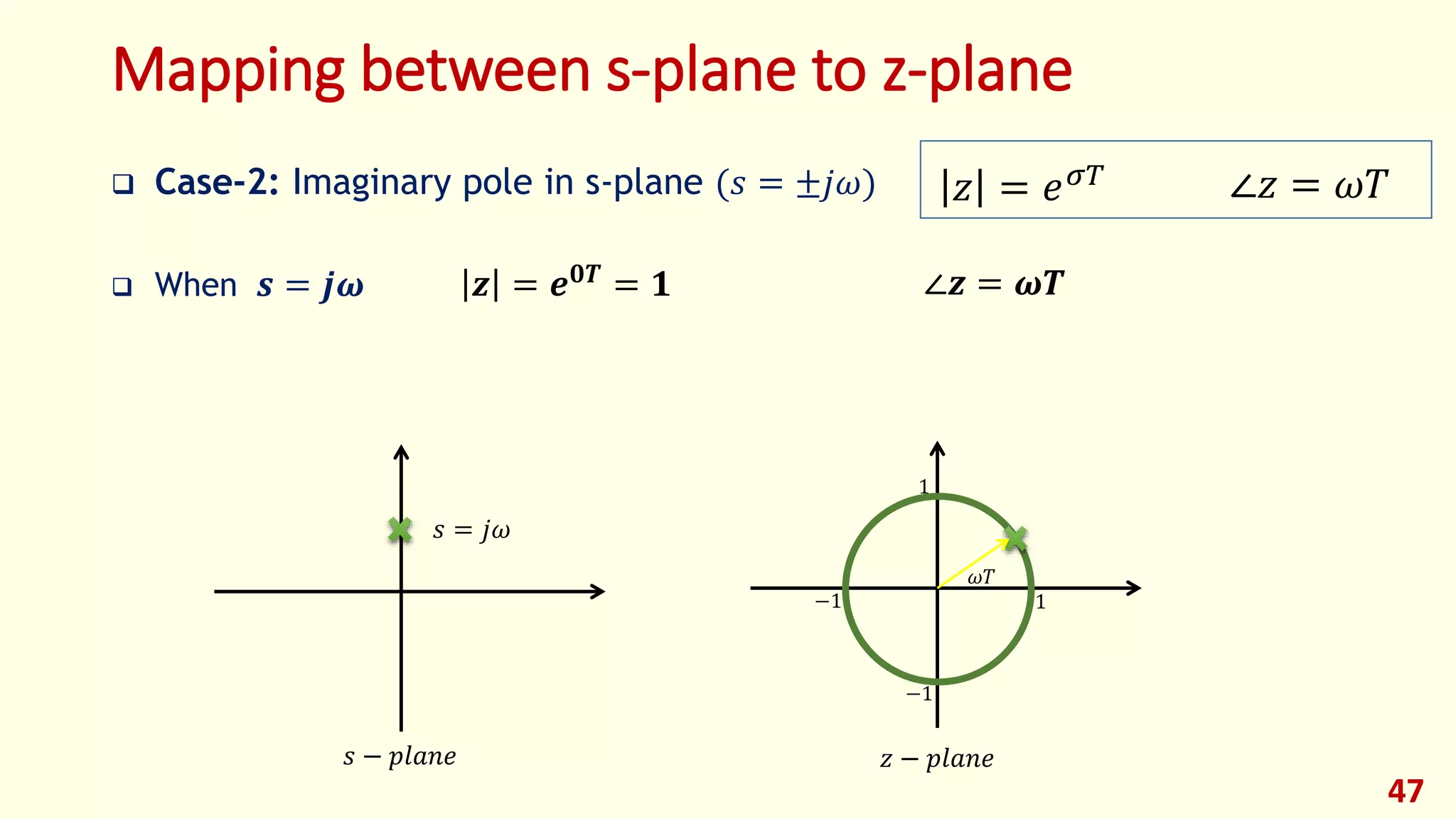
 Case-2: Imaginary Pole in s-plane (𝑠 = 𝑗𝜔)
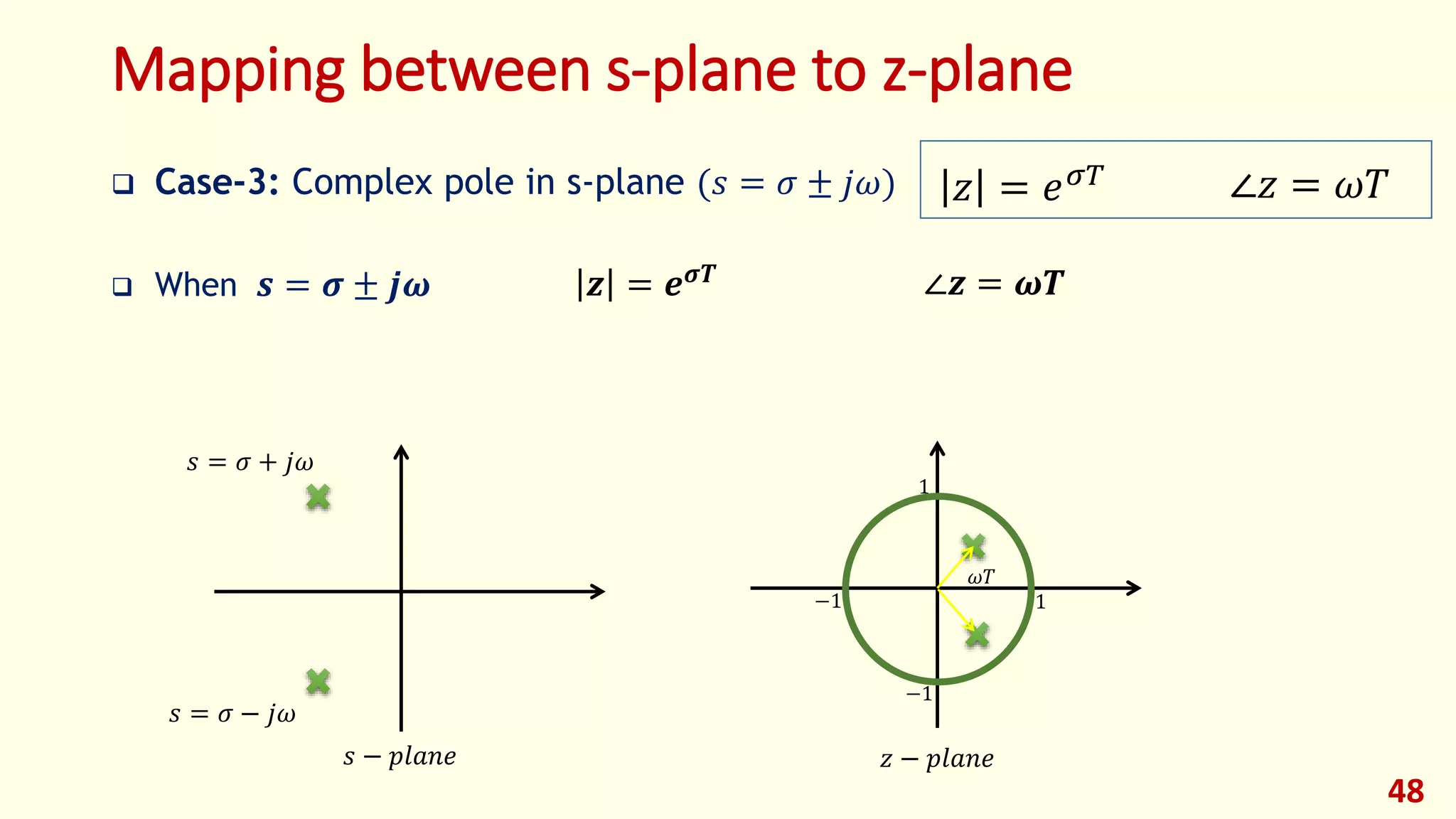
 Case-3: Complex Poles (𝑠 = 𝜎 + 𝑗𝜔)
45𝑠 − 𝑝𝑙𝑎𝑛𝑒 𝑧 − 𝑝𝑙𝑎𝑛𝑒

46. Mapping between s-plane to z-plane
 Case-1: Real pole in s-plane (𝑠 = 𝜎)
 When 𝑠 = 0
 When 𝑠 = −∞
46
∠𝑧 = 𝜔𝑇𝑧 = 𝑒 𝜎 𝑇
𝑧 = 𝑒0𝑇 = 1 ∠𝑧 = 0𝑇 = 0
𝑠 = 0
𝑠 − 𝑝𝑙𝑎𝑛𝑒 𝑧 − 𝑝𝑙𝑎𝑛𝑒
1
𝑧 = 𝑒−∞𝑇 = 1 ∠𝑧 = 0𝑇 = 0

47. Mapping between s-plane to z-plane
 Case-2: Imaginary pole in s-plane (𝑠 = ±𝑗𝜔)
 When 𝒔 = 𝒋𝝎
47
∠𝑧 = 𝜔𝑇𝑧 = 𝑒 𝜎𝑇
𝒛 = 𝒆 𝟎𝑻 = 𝟏 ∠𝒛 = 𝝎𝑻
𝑠 = 𝑗𝜔
𝑠 − 𝑝𝑙𝑎𝑛𝑒 𝑧 − 𝑝𝑙𝑎𝑛𝑒
1
−1
−1
1
𝜔𝑇

48. Mapping between s-plane to z-plane
 Case-3: Complex pole in s-plane (𝑠 = 𝜎 ± 𝑗𝜔)
 When 𝒔 = 𝝈 ± 𝒋𝝎
48
∠𝑧 = 𝜔𝑇𝑧 = 𝑒 𝜎𝑇
𝒛 = 𝒆 𝝈𝑻 ∠𝒛 = 𝝎𝑻
𝑠 = 𝜎 + 𝑗𝜔
𝑠 − 𝑝𝑙𝑎𝑛𝑒 𝑧 − 𝑝𝑙𝑎𝑛𝑒
1
−1
−1
1
𝜔𝑇
𝑠 = 𝜎 − 𝑗𝜔

49. Mapping Regions of the s-plane onto the z-plane
49

50. 50