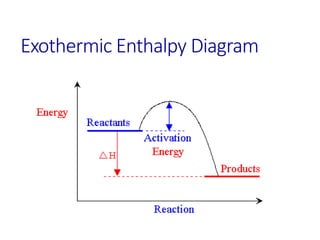
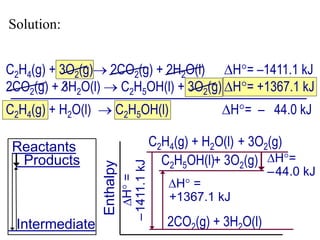
Hess's law states that the total enthalpy change for a reaction is equal to the sum of the enthalpy changes of the steps that make up that reaction. This allows one to calculate the enthalpy of a reaction from standard enthalpy of formation values without directly measuring the enthalpy change experimentally. Enthalpy diagrams can be used to visually represent how individual reaction steps add together based on Hess's law.

1. Hess’s Law

2. CalculatingEnthalpiesof Reactions
• The basis for calculating enthalpies of reaction is
known as Hess’s law: the overall enthalpy
change in a reaction is equal to the sum of
enthalpy changes for the individual steps in the
process.
• This means that the energy difference between
reactants and products is independent of the
route taken to get from one to the other.

3. If you know the reaction enthalpies of individual steps in an
overall reaction, you can calculate the overall enthalpy without
having to measure it experimentally.

4. Calculate thepotential energy of each climber takingroute
1 androute 2
-137KJ
+125KJ
+87KJ
-193KJ
+102KJ
-163KJ
+52KJ
-147KJ
-269KJ
+7KJ
Regardless of the route the climber and the miner
took they ended up having the same amount of
potential energy!!

5. Hess’s Law
Start
Finish
A State Function: Path independent.
Both lines accomplished the same result, they went
from start to finish.
Net result = same.

6. ∆Htarget = ∑∆Hknown
∆Htarget =∆Hrxn1+∆Hrxn2+∆Hrxn3+...
Hess’s Law Equation:

7. For example: C + O2  CO2
occurs as 2 steps
C + ½O2  CO H = – 110.5 kJ
CO + ½O2  CO2 H = – 283.0 kJ
C + CO + O2  CO + CO2 H = – 393.5 kJ
C + O2  CO2 H = – 393.5 kJ

8. Using Hess’s Law to find ΔH
What is the enthalpy change for the formation of two moles of
nitrogen monoxide from its elements?
This reaction may be called the target equation to
distinguish it clearly from other equations
N2(g) + O2(g) 2NO (g)
1. ½ N2(g) + O2(g) NO2(g) ΔH1
θ = +34 kJ
2. NO(g) + ½ O2(g) NO2(g) ΔH2
θ = - 56 kJ

9. If we work with these two equations, which may be
called known equations, and then add them together,
we obtain the chemical equation for the formation of
nitrogen monoxide
N2(g) + O2(g) 2NO (g)
If we look at the target eqn., it has 1 mole of N2 as
reactant. How do we make it 1 mole?

10. 2 x (½ N2(g) + O2(g) NO2(g) ΔH1
θ = 2(+34 )kJ
2 x (NO2 (g) NO(g) + ½ O2(g) ΔH2
θ = 2(+ 56 )kJ
N2(g) + 2O2(g) 2 NO2(g) ΔH1
θ = 2(+34 )kJ
2 NO2 (g) 2NO(g) + O2(g) ΔH2
θ = 2(+ 56 )kJ
N2(g) + 2O2(g) + 2NO2(g) 2NO2(g) + 2NO(g) + O2(g)
N2(g) + O2(g) 2NO(g)

11. ∆Hθ = 2(+ 34) kJ + 2(+ 56) kJ
= + 68 kJ + 112 kJ
∆Hθ = + 180 kJ

12. • To demonstrate how to apply Hess’s law, we will work
through the calculation of the enthalpy of formation for the
formation of methane gas, CH4, from its elements,
hydrogen gas and solid carbon:
C(s) + 2H2(g) → CH4(g)
fH0
? 

13. • The component reactions in this case are the
combustion reactions of carbon, hydrogen, and
methane:
0
393.5 kJcH  
0
285.8 kJcH  
0
890.8 kJcH  
H2(g) + ½O2(g) → H2O(l)
C(s) + O2(g) → CO2(g)
CH4(g) + 2O2(g) → CO2(g) + 2H2O(l)
• The overall reaction involves the formation rather than the
combustion of methane, so the combustion equation for
methane is reversed, and its enthalpy changed from
negative to positive:
CO2(g) + 2H2O(l) → CH4(g) + 2O2(g) ∆H0 = +890.8 kJ

14. • Because 2 moles of water are used as a reactant in the above
reaction, 2 moles of water will be needed as a product.
• Therefore, the coefficients for the formation of water reaction,
as well as its enthalpy, need to be multiplied by 2:
2H2(g) + O2(g) → 2H2O(l) cH0
2( 285.8 kJ)  
• We are now ready to add the three equations together using
Hess’s law to give the enthalpy of formation for methane and
the balanced equation.
0
393.5 kJcH  
0
2( 285.8 kJ)cH  
0
74.3 kJfH  
2H2(g) + O2(g) → 2H2O(l)
C(s) + O2(g) → CO2(g)
C(s) + 2H2(g) → CH4(g)
CO2(g) + 2H2O(l) → CH4(g) + 2O2(g) ΔHθ = +890.8 kJ

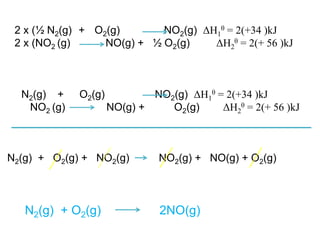
15. • Using Hess’s law, any enthalpy of reaction may be
calculated using enthalpies of formation for all the
substances in the reaction of interest, without
knowing anything else about how the reaction occurs.
• Mathematically, the overall equation for enthalpy
change will be in the form of the following equation:
∆H0 = sum of [( of products) × (mol of products)]
– sum of [( of reactants) × (mol of reactants)]
fH0

fH0


16. Hess’s law allows us to add equations.
We add all reactants, products, & H values.
We can also show how these steps add together via an
“enthalpy diagram” …

17. Exothermic Enthalpy Diagram

18. Endothermic Enthalpy Diagram

19. Steps in drawing enthalpy diagrams
1. Balance the equation(s).
2. Sketch a rough draft based on H values.
3. Draw the overall chemical reaction as an enthalpy diagram
(with the reactants on one line, and the products on the other
line).

20. 4. Draw a reaction representing the intermediate step
by placing the relevant reactants on a line.
5. Check arrows:
Start: two leading away
Finish: two pointing to finish
Intermediate: one to, one away
6. Look at equations to help complete balancing (all
levels must have the same # of all atoms).
7. Add axes and H values.

21. C + O2  CO2 H = – 393.5 kJ
Reactants
Intermediate
Products
C + O2
CO2
CO
Enthalpy
Note: states such as (s) and (g) have been ignored to reduce
clutter on these slides. You should include these in your work.
H = – 110.5 kJ
H =
– 283.0 kJ
H =
– 393.5 kJ
+ ½O2
C + ½O2  CO H = – 110.5 kJ
CO + ½O2  CO2 H = – 283.0 kJ

22. HowmuchenergyislostintheformationofC2H5OH(l) ?
C2H4(g) +H2O(l)C2H5OH(l)
Given:
C2H4(g) + 3O2(g) 2CO2(g) + 2H2O(l)
H= –1411.1 kJ
2CO2(g) + 3H2O(l)  C2H5OH(l) + 3O2(g)
H= +1367.1 kJ

23. C2H4(g) + 3O2(g) 2CO2(g) + 2H2O(l) H= –1411.1 kJ
2CO2(g) + 3H2O(l)  C2H5OH(l) + 3O2(g) H= +1367.1 kJ
C2H4(g) + H2O(l)  C2H5OH(l)
Reactants
Products
Intermediate
C2H4(g) + H2O(l)
C2H5OH(l)
2CO2(g) + 3H2O(l)
Enthalpy
H=
–1411.1kJ
H =
+1367.1 kJ
H=
–44.0 kJ
+ 3O2(g)
+ 3O2(g)
H= – 44.0 kJ
Solution:

24. Two Rules to Follow:
1. If a chemical equation is reversed, then the sign of ∆H
changes
2. If the coefficients of a chemical equation are altered by
multiplying or dividing by a constant factor, then the value of
∆H is altered in the same way

25. We may need to manipulate equations further: 2Fe +
1.5O2  Fe2O3 H=?,
Given:
Fe2O3 + 3CO  2Fe + 3CO2 H= – 26.74 kJ
CO + ½O2  CO2 H= –282.96 kJ
1: Align equations based on reactants/products.
2: Multiply based on final reaction.
3: Add equations.
2Fe + 1.5O2  Fe2O3
3CO + 1.5O2  3CO2 H= –848.88 kJ
2Fe + 3CO2  Fe2O3 + 3CO H= + 26.74 kJ
CO + ½O2  CO2 H= –282.96 kJ
H= –822.14 kJ
Flip equation =Flip sign
Multiply coefficients and values

26. Sample Problem B
Calculate the enthalpy of reaction for the combustion of nitrogen
monoxide gas, NO, to form nitrogen dioxide gas, NO2, as given in
the following equation.
NO(g) + ½O2(g) → NO2(g)
Use the enthalpy-of-formation data. Solve by combining the known
thermochemical equations.
Given: ½ N2(g) + ½ O2(g) NO(g) ∆Hf
θ +90.29 kJ
½ N2(g) + O2(g) NO2(g) ∆Hf
θ +33.2 kJ
Unknown: ∆Hθ for NO(g) + ½ O2(g) NO2(g)
Solution:
Using Hess’s law, combine the given thermochemical equations in
such a way as to obtain the unknown equation, and its ∆H0 value.

27. The desired equation is:
g + g g1
2 22
NO( ) O ( ) NO ( )
 g g + g = k1 1
22 2 f2
0
NO( ) N ( ) O ( H – 90.29) J
g g g k01
2 2 2 f2
N ( ) + O ( ) NO ( ) ΔH =+33.2 J
The other equation should have NO2 as a product, so
we can use the second given equation as is:
Reversing the first given reaction and its sign yields the
following thermochemical equation:

28. We can now add the equations and their ∆H0 values to
obtain the unknown ∆H0 value.
g g g k01
2 2 2 f2
N ( ) + O ( ) NO ( ) H =+33.2 J 
 g g + g = k1 1
22 2 f2
0
NO( ) N ( ) O ( H – 90.29) J
0
57.1 kJH  g + g g1
2 22
NO( ) O ( ) NO ( )

29. Determining Enthalpy of Formation
• When carbon is burned in a limited supply of
oxygen, carbon monoxide is produced:
s + g g1
22
C( ) O ( ) CO( )
• The above overall reaction consists of two
reactions:
1) carbon is oxidized to carbon dioxide
2) carbon dioxide is reduced to give carbon
monoxide.

30. • Because these two reactions occur simultaneously, it is not
possible to directly measure the enthalpy of formation of
CO(g) from C(s) and O2(g).
• We do know the enthalpy of formation of carbon dioxide and
the enthalpy of combustion of carbon monoxide:
fH0
2 2C(s) + O (g) CO (g) 393.5 kJ/mol   
cg g g H01
2 22
CO( ) + O ( ) CO ( ) 283.0 kJ/mol   
g g g H01
2 22
CO ( ) CO( ) + O ( ) 283.0 kJ/mol   
H0
2 2C(s) + O (g) CO (g) 393.5 kJ/mol   
• We reverse the second equation because we need CO as
a product. Adding gives the desired enthalpy of formation
of carbon monoxide.
0
110.5 kJH  s + g g1
22
C( ) O ( ) CO( )

31. Determine the heat of reaction for the reaction:
Target  4NH3(g) + 5O2(g)  4NO(g) + 6H2O(g) H= ?
Using the following sets of reactions:
(1) N2(g) + O2(g)  2NO(g) H = 180.6 kJ
(2) N2(g) + 3H2(g)  2NH3(g) H = -91.8 kJ
(3) 2H2(g) + O2(g)  2H2O(g) H = -483.7 kJ
Hint: The three reactions must be algebraically
manipulated to sum up to the desired reaction.
and.. the H values must be treated accordingly.

32. 4NH3(g) + 5O2(g)  4NO(g) + 6H2O(g)
Using the following sets of reactions:
(1) N2(g) + O2(g)  2NO(g) H = 180.6 kJ
(2) N2(g) + 3H2(g)  2NH3(g) H = -91.8 kJ
(3) 2H2(g) + O2(g)  2H2O(g) H = -483.7 kJ
Goal:
NH3:
O2 :
NO:
H2O:
(2)(Reverse and x 2) 4NH3  2N2 + 6H2 H = +183.6 kJ
Found in more than one place, SKIP IT (its hard).
(1) (Same x2) 2N2 + 2O2  4NO H = 361.2 kJ
(3)(Same x3) 6H2 + 3O2  6H2O H = -1451.1 kJ

33. 4NH3(g) + 5O2(g)  4NO(g) + 6H2O(g)Goal:
NH3:
O2 :
NO:
H2O:
Reverse and x2 4NH3  2N2 + 6H2 H = +183.6 kJ
Found in more than one place, SKIP IT.
x2 2N2 + 2O2  4NO H = 361.2 kJ
x3 6H2 + 3O2  6H2O H = -1451.1 kJ
Cancel terms and take sum.
4NH3
+ 5O2  4NO + 6H2O H = -906.3 kJ
Is the reaction endothermic or exothermic?
H = 183.6 kJ + 361.2 kJ + (-1451kJ)

34. Determine the heat of reaction for the reaction:
TARGET  C2H4(g) + H2(g)  C2H6(g) H = ?
Use the following reactions:
(1) C2H4(g) + 3O2(g)  2CO2(g) + 2H2O(l) H = -1401 kJ
(2) C2H6(g) + 7/2O2(g)  2CO2(g) + 3H2O(l)H = -1550 kJ
(3) H2(g) + 1/2O2(g)  H2O(l) H = -286 kJ
Consult your neighbour if necessary.

35. Determine the heat of reaction for the reaction:
Goal: C2H4(g) + H2(g)  C2H6(g) H = ?
Use the following reactions:
(1) C2H4(g) + 3O2(g)  2CO2(g) + 2H2O(l) H = -1401 kJ
(2) C2H6(g) + 7/2O2(g)  2CO2(g) + 3H2O(l) H = -1550 kJ
(3) H2(g) + 1/2O2(g)  H2O(l) H = -286 kJ
C2H4(g) :use 1 as is C2H4(g) + 3O2(g)  2CO2(g) + 2H2O(l) H = -1401 kJ
H2(g) :# 3 as is H2(g) + 1/2O2(g)  H2O(l) H = -286 kJ
C2H6(g) : rev #2 2CO2(g) + 3H2O(l)  C2H6(g) + 7/2O2(g) H = +1550 kJ
C2H4(g) + H2(g)  C2H6(g) H = -137 kJ

36. Hess’s Law Example Problem
Calculate H for the combustion of methane, CH4
using the equations above
Ans = -890.36 kJ
Reaction Hf
o
C + 2H2  CH4 -74.80 kJ
C + O2  CO2 -393.50 kJ
H2 + ½ O2  H2O -285.83 kJ