The document discusses solutions to Euler equations, which are differential equations of the form 0][ 2=+′+′′= yyxyxyL βα. It provides the general solutions based on whether the roots r1 and r2 of the characteristic equation are real/distinct, equal, or complex. For initial value problems, the constants in the general solution are determined using the given initial conditions. Near the singular point x=0, the qualitative behavior of the solutions depends on the nature of the roots r1 and r2.

1. Ch 5.5: Euler Equations
A relatively simple differential equation that has a regular
singular point is the Euler equation,
where α, β are constants.
Note that x0 = 0 is a regular singular point.
The solution of the Euler equation is typical of the solutions
of all differential equations with regular singular points, and
hence we examine Euler equations before discussing the
more general problem.
0][ 2
=+′+′′= yyxyxyL βα

2. Solutions of the Form y = xr
In any interval not containing the origin, the general solution
of the Euler equation has the form
Suppose x is in (0, ∞), and assume a solution of the form
y = xr
. Then
Substituting these into the differential equation, we obtain
or
or
)()()( 2211 xycxycxy +=
21
)1(,, −−
−=′′=′= rrr
xrryxryxy
0)1(][ =++−= rrrr
xxrxrrxL βα
[ ] 0)1(][ 2
=+−+= βα rrxxL rr
[ ] 0)1(][ =++−= βα rrrxxL rr
0][ 2
=+′+′′= yyxyxyL βα

3. Quadratic Equation
Thus, after substituting y = xr
into our differential equation,
we arrive at
and hence
Let F(r) be defined by
We now examine the different cases for the roots r1, r2.
( ) 0,0)1(2
>=+−+ xrrxr
βα
))(()1()( 21
2
rrrrrrrF −−=+−+= βα
2
4)1()1( 2
βαα −−±−−
=r

4. Real, Distinct Roots
If F(r) has real roots r1 ≠ r2, then
are solutions to the Euler equation. Note that
Thus y1 and y2 are linearly independent, and the general
solution to our differential equation is
21
)(,)( 21
rr
xxyxxy ==
( ) .0allfor01
12
1
1
1
2
1
2
1
121
21
21
2121
21
21
>≠−=
−=
=
′′
=
−+
−+−+
−−
xxrr
xrxr
xrxr
xx
yy
yy
W
rr
rrrr
rr
rr
0,)( 21
21 >+= xxcxcxy rr

5. Example 1
Consider the equation
Substituting y = xr
into this equation, we obtain
and
Thus r1 = -1/3, r2 = 1, and our general solution is
21
)1(,, −−
−=′′=′= rrr
xrryxryxy
[ ]
[ ]
( )( ) 0113
0123
01)1(3
0)1(3
2
=−+
=−−
=−+−
=−+−
rrx
rrx
rrrx
xrxxrr
r
r
r
rrr
0,)( 2
3/1
1 >+= −
xxcxcxy
0,03 2
>=−′+′′ xyyxyx

6. Equal Roots
If F(r) has equal roots r1 = r2, then we have one solution
We could use reduction of order to get a second solution;
instead, we will consider an alternative method.
Since F(r) has a double root r1, F(r) = (r - r1)2
, and F'(r1) = 0.
This suggests differentiating L[xr
] with respect to r and then
setting r equal to r1, as follows:
1
)(1
r
xxy =
[ ] ( )
( )
( ) ( )
0,ln)(
2ln]ln[
][
)1(][
1
2
1
2
1
2
1
2
1
2
>=⇒
−+−=
−
∂
∂
=
∂
∂
−=+−+=
xxxxy
xrrrrxxxxL
rrx
r
xL
r
rrxrrxxL
r
rrr
rr
rrr
βα

7. Equal Roots
Thus in the case of equal roots r1 = r2, we have two solutions
Now
Thus y1 and y2 are linearly independent, and the general
solution to our differential equation is
xxxyxxy rr
ln)(,)( 11
21 ==
( )
( )
.0allfor0
ln1ln
1ln
ln
12
12
11
12
1
11
121
21
1
11
11
11
>≠=
−+=
+
=
′′
=
−
−−
−−
xx
xxrxrx
xrxxr
xxx
yy
yy
W
r
rr
rr
rr
( ) 0,lnln)( 111
2121 >+=+= xxxccxxcxcxy rrr

8. Example 2
Consider the equation
Then
and
Thus r1 = r2 = -3, our general solution is
21
)1(,, −−
−=′′=′= rrr
xrryxryxy
0,0972
>=+′+′′ xyyxyx
[ ]
[ ]
( ) 03
096
097)1(
097)1(
2
2
=+
=++
=++−
=++−
rx
rrx
rrrx
xrxxrr
r
r
r
rrr
( ) 0,ln)( 3
21 >+= −
xxxccxy

9. Complex Roots
Suppose F(r) has complex roots r1 = λ + iµ, r2 = λ - iµ,
with µ ≠ 0. Then
Thus xr
is defined for complex r, and it can be shown that the
general solution to the differential equation has the form
However, these solutions are complex-valued. It can be
shown that the following functions are solutions as well:
( )
( ) ( )[ ] 0,lnsinlncoslnln
lnlnlnlnln
>+==
==== +
xxixxee
eeeeex
xix
xixxixrxr r
µµλµ
µλµλ
λ
0,)( 21 >+= −+
xxcxcxy ii µλµλ
( ) ( )xxxyxxxy lnsin)(,lncos)( 21 µµ λλ
==

10. Complex Roots
The following functions are solutions to our equation:
Using the Wronskian, it can be shown that y1 and y2 are
linearly independent, and thus the general solution to our
differential equation can be written as
( ) ( )xxxyxxxy lnsin)(,lncos)( 21 µµ λλ
==
( ) ( ) 0,lnsinlncos)( 21 >+= xxxcxxcxy µµ λλ

11. Example 3
Consider the equation
Then
and
Thus r1 = -2i, r2 = 2i, and our general solution is
0,042
>=+′+′′ xyyxyx
21
)1(,, −−
−=′′=′= rrr
xrryxryxy
[ ]
[ ] 04
04)1(
04)1(
2
=+
=++−
=++−
rx
rrrx
xrxxrr
r
r
rrr
( ) ( )
( ) ( ) 0,ln2sinln2cos
ln2sinln2cos)(
21
0
2
0
1
>+=
+=
xxcxc
xxcxxcxy

12. Solution Behavior
Recall that the solution to the Euler equation
depends on the roots:
where r1 = λ + iµ, r2 = λ - iµ.
The qualitative behavior of these solutions near the singular
point x = 0 depends on the nature of r1 and r2. Discuss.
Also, we obtain similar forms of solution when t < 0. Overall
results are summarized on the next slide.
( )
( ) ( ),lnsinlncos)(:complex,
ln)(:
)(:
2121
2121
2121
1
21
xxcxxcxyrr
xxccxyrr
xcxcxyrr
r
rr
µµ λλ
+=
+==
+=≠
0][ 2
=+′+′′= yyxyxyL βα

13. Theorem 5.5.1
The general solution to the Euler equation
in any interval not containing the origin is determined by the
roots r1 and r2 of the equation
according to the following cases:
where r1 = λ + iµ, r2 = λ - iµ.
( )
( ) ( ),lnsinlncos)(:complex,
ln)(:
)(:
2121
2121
2121
1
21
xxcxxcxyrr
xxccxyrr
xcxcxyrr
r
rr
µµ λλ
+=
+==
+=≠
02
=+′+′′ yyxyx βα
))(()1()( 21
2
rrrrrrrF −−=+−+= βα

14. Shifted Equations
The solutions to the Euler equation
are similar to the ones given in Theorem 5.5.1:
where r1 = λ + iµ, r2 = λ - iµ.
( )
( ) ( ),lnsinlncos)(
:complex,
ln)(:
)(:
02001
21
002121
020121
1
21
xxxcxxxxcxy
rr
xxxxccxyrr
xxcxxcxyrr
r
rr
−+−−=
−−+==
−+−=≠
µµ λλ
( ) ( ) 00
2
0 =+′−+′′− yyxxyxx βα

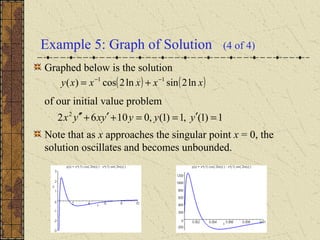
15. Example 5: Initial Value Problem (1 of 4)
Consider the initial value problem
Then
and
Using the quadratic formula on r2
+ 2r + 5, we obtain
1)1(,1)1(,01062 2
=′==+′+′′ yyyyxyx
21
)1(,, −−
−=′′=′= rrr
xrryxryxy
[ ]
[ ] 01042
0106)1(2
0106)1(2
2
=++
=++−
=++−
rrx
rrrx
xrxxrr
r
r
rrr
ir 21
2
2042
±−=
−±−
=

16. Example 5: General Solution (2 of 4)
Thus λ = -1, µ = 2, and the general solution of our initial
value problem is
where the last equality follows from the requirement that the
domain of the solution include the initial point x = 1.
To see this, recall that our initial value problem is
( ) ( )
( ) ( ),ln2sinln2cos
ln2sinln2cos)(
1
2
1
1
1
2
1
1
xxcxxc
xxcxxcxy
−−
−−
+=
+=
1)1(,1)1(,01062 2
=′==+′+′′ yyyyxyx

17. Example 5: Initial Conditions (3 of 4)
Our general solution is
Recall our initial value problem:
Using the initial conditions and calculus, we obtain
Thus our solution to the initial value problem is
( ) ( )xxcxxcxy ln2sinln2cos)( 1
2
1
1
−−
+=
1,1
12
1
21
21
1
==⇒



=+−
=
cc
cc
c
( ) ( )xxxxxy ln2sinln2cos)( 11 −−
+=
1)1(,1)1(,01062 2
=′==+′+′′ yyyyxyx

18. Example 5: Graph of Solution (4 of 4)
Graphed below is the solution
of our initial value problem
Note that as x approaches the singular point x = 0, the
solution oscillates and becomes unbounded.
( ) ( )xxxxxy ln2sinln2cos)( 11 −−
+=
1)1(,1)1(,01062 2
=′==+′+′′ yyyyxyx