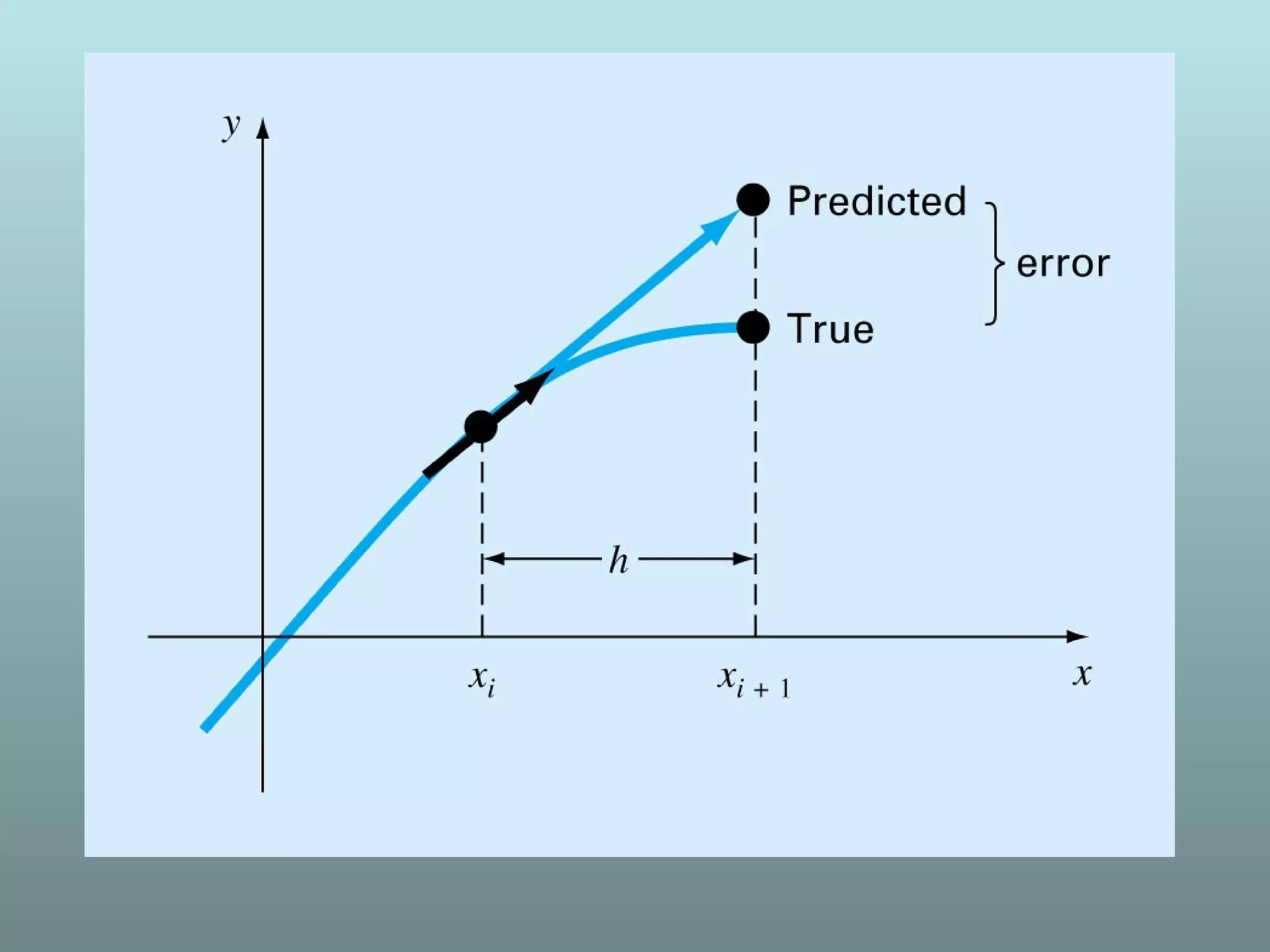
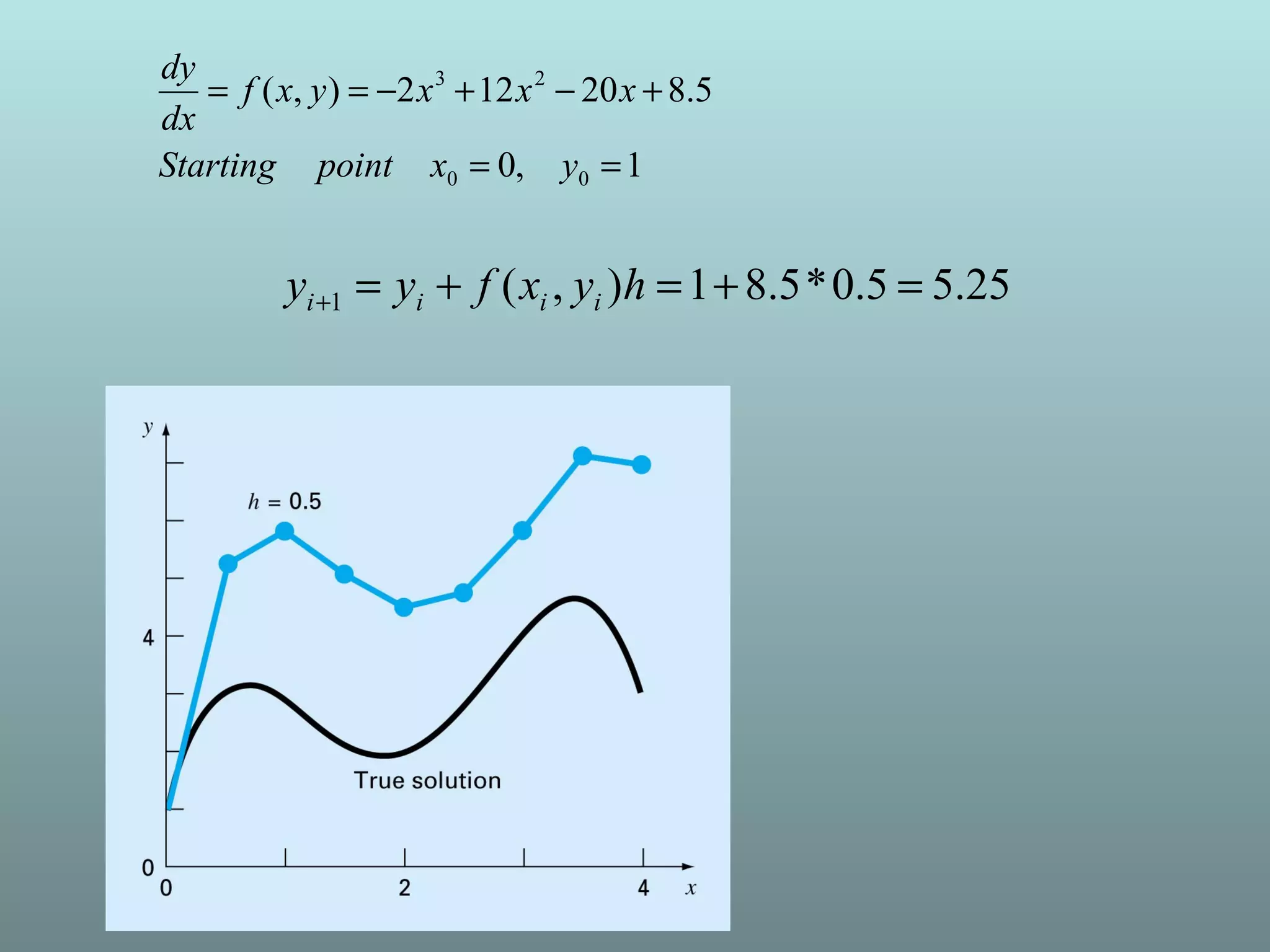
This document provides an introduction to differential equations. It defines a differential equation as an equation containing an unknown function and its derivatives. Ordinary differential equations are presented, along with definitions of the order and degree of a differential equation. Methods for solving differential equations are introduced, including Taylor series methods, Euler's method, and error analysis. Examples are provided to demonstrate applying these methods.

1. Introduction to DifferentialIntroduction to Differential
EquationsEquations
Prepared By :-
Divyanshi Bagrawala - 130420105003
Bhaumik Parikh - 130420105006
Bhumika Jariwala - 130420105019
Juhi Kala - 130420105025
Keval dalsaniya - 130420105030
Vishvaraj Chauhan - 130420105058

2. Definition:
A differential equation is an equation containing an unknown function
and its derivatives.
Equations which are composed of an unknown function and its derivatives are
called differential equations.
32 += x
dx
dy
032
2
=++ ay
dx
dy
dx
yd
36
4
3
3
=+





+ y
dx
dy
dx
yd
Examples:-
y is dependent variable and x is independent variable,
and these are ordinary differential equations
1.
2.
3.
Ordinary Differential Equations

3. Order of Differential Equation
The order of the differential equation is order of the highest
derivative in the differential equation.
Differential Equation ORDER
32 += x
dx
dy
0932
2
=++ y
dx
dy
dx
yd
36
4
3
3
=+





+ y
dx
dy
dx
yd
1
2
3

4. Degree of Differential Equation
Differential Equation Degree
032
2
=++ ay
dx
dy
dx
yd
36
4
3
3
=+





+ y
dx
dy
dx
yd
03
53
2
2
=+





+





dx
dy
dx
yd
1
1
3
The degree of a differential equation is power of the highest
order derivative term in the differential equation.

5. Solution of Differential EquationSolution of Differential Equation

6. Taylor's Series method
Consider the one dimensional initial value problem
y' = f(x, y), y(x0
) = y0
where f is a function of two variables x and y and (x0
, y0
) is a known point on the
solution curve.
•If the existence of all higher order partial derivatives is assumed for y at x = x0
, then by
Taylor series the value of y at any neibhouring point x+h can be written as
y(x0
+h) = y(x0
) + h y'(x0
) + h2
/2 y''(x0
) + h3
/3! y'''(x0
) + . . . . . .
•where ' represents the derivative with respect to x. Since at x0
, y0
is known, y' at x0
can
be found by computing f(x0
,y0
). Similarly higher derivatives of y at x0
also can be
computed by making use of the relation
y' = f(x,y)
y'' = fx
+ fy
y'
y''' = fxx
+ 2fxy
y' + fyy
y'2
+ fy
y''
and so on.
Then
y(x0
+h) = y(x0
) + h f + h2
( fx
+ fy
y' ) / 2! + h3
( fxx
+ 2fxy
y' + fyy
y'2
+ fy
y'' ) / 3! + o(h4
)
Hence the value of y at any neighboring point x0
+ h can be obtained by summing the

7. Example: 1
Solve the initial value problem y' = -2xy2
, y(0) = 1 for y at x = 1 with step length 0.2 using Taylor series
method of order four.
Solution:
Given y' = f(x,y) = -2xy2
Þ y'' = -2y2
- 4xyy'
y''' = -8yy' - 4xy'2
- 4xyy''
yiv
= -12y'2
- 12yy'' - 12xy'y'' - 4xyy'''
yv
= -48y'y'' - 16yy''' -12xy''2
- 16xy'y''' - 4xyyiv
The forth order Taylor's formula is
y(xi+h) = y(xi) + h y'(xi, yi) + h2
y''(xi, yi)/2! + h3
y'''(xi, yi)/3! + h4
yiv
(xi, yi)/4!
given at x=0, y=1 and with h = .2 we have
y' = -2(0)(1)2
= 0.0
y'' = -2(1)2
- 4(0)(1)(0) = -2
y''' = -8(1)(0) - 4(0)(0)2
- 4(0)(1)(-2) = 0.0
yiv
= -12(0)2
- 12(1)(-2) - 12(0)(0)(-2) - 4(0)(1)(0) = 24
y(0.2) = 1 + .2 (0) + .22
(-2)/2! + 0 + .24
(24)/4! = .9615
now at x = .2 we have y = .9615
y' = -0.3699, y'' = -1.5648, y''' = 3.9397 and yiv
= 11.9953
then y(0.4) = 1 + .2 (-.3699) + .22
(-1.5648)/2! + .23
(3.9397)/3! + .24
(11.9953)/4! = 0.8624
y(0.6) = 1 + .2 (-.5950) + .22
(-0.6665)/2! + .23
(4.4579)/3! + .24
(-5.4051)/4! = 0.7356
y(0.8) = 1 + .2 (-.6494) + .22
(-0.0642)/2! + .23
(2.6963)/3! + .24
(-10.0879)/4! = 0.6100
y(1.0) = 1 + .2 (-.5953) + .22
(-0.4178)/2! + .23
(0.9553)/3! + .24
(-6.7878)/4! = 0.5001

8. now at x = 1.0 we have y = .5001
y' = -0.5001,
y'' = 0.5004,
y''' = -.000525 and yiv
= -3.0005
Error in the approximation
E4 = h4
(y4
(1.0) - y4
(0.8))/ 5! = h4
(-3.0005-11.9953)/ 5! = -1.9994e-004
Analytical solution y(x) = 1/(1+x2
) at x = 1, y = .5
Alternate method:
By Taylor series method
y(x0 + x - x0) = y0 + (x-x0)y'(x0) + (x-x0)2
y''(x0)/2! + (x-x0)3
y'''(x0)/3! + (x-
x0)4
yiv
(x0)/4! + . . .
Since x0 = y' = y''' = 0, y = 1, y'' = -2 and yiv
= 24 at x = 0,
y( x ) = 1. - x2
+ x4
+ . . .

9. Example 2:
Using Taylor series method, find y(0.1) for y' = x - y2
, y(0) = 1 correct upto four
decimal places.
Solution:
Given y' = f(x,y) = x - y2
y'' = 1 - 2yy', y''' = -2yy'' - 2y'2
, yiv
= -2yy''' - 6y'y'', yv
= -2yyiv
-8y'y''' -6y''2
Since at x = 0, y = 1;
y' = -1, y'' = 3, y''' = -8, yiv
= 34 and yv
= -186
The forth order Taylor's formula is
y(x) = y(x0) + (x-x0) y'(x0, y0) + (x-x0)2
y''(x0, y0)/2! + (x-x0)3
y'''(x0, y0)/3! +
(x-x0)4
yiv
(x0, y0)/4! + h5
yv
(x0, y0)/5! +.
. .
= 1 - x + 3 x2
/2! - 8 x3
/3! + 34 x4
/4! - 186 x5
/5! (since x0 = 0)
= 1 - x + 3 x2
/2 - 4 x3
/3 + 17 x4
/12 - 31 x5
/20
Now
y(0.1) = 1 - (0.1) + 3 (0.1)2
/2 - 4 (0.1)3
/3 + 17 (0.1)4
/12 - 31 (0.1)5
/20
= 0.9 + 3 (0.1)2
/2 - 4 (0.1)3
/3 + 17 (0.1)4
/12 - 31 (0.1)5
/20
= 0.915 - 4 (0.1)3
/3 + 17 (0.1)4
/12 - 31 (0.1)5
/20
= 0.9137 + 17 (0.1)4
/12 - 31 (0.1)5
/20
= 0.9138 - 31 (0.1)5
/20
= 0.9138

10. Euler’s Method
Though in principle it is possible to use Taylor's method of
any order for the given initial value problem to get good
approximations, it has few draw backs like
•The scheme assumes the existence of all higher order
derivatives for the given function f(x,y) which is not a
requirement for the existence of the solution for any first
order initial value problem.
•Even the existence of these higher derivatives is guaranteed
it may not be easy to compute them for any given f(x,y).
•Because of the usage of higher order derivatives in the
formula it is not convenient to write computer programs , that
is the method is more suited for hand calculations.

11. To overcome these difficulties, Euler developed a scheme by
approximating y' in the given ivp. The scheme is as follows:
The derivative term in the first order ivp
y' = f(x, y) , y(x0
) = y0
is approximated by making use of Taylor series approximation of the
dependent variable y(x) at the point xi+1
. That is
y(xi+1
) = y(xi
+ ∆x) = y(xi
) + ∆xy'(xi
) + (∆x2
/ 2)y''(xi
) + . . .
= y(xi
) + ∆xf(xi
, yi
) + (∆x2
/ 2)y''(xi
) + . . .
(... y'(xi
) = f(xi
, yi
))
if the infinite series is truncated from the term ∆x2
onwards, then
y(xi+1
) = y(xi
) + ∆x y'(xi
) (or)
yi+1
= yi
+ ∆x fi
for all i
That is,
for i = 0, y1
= y0
+ ∆x f0
i = 1, y2
= y1
+ ∆x f1
i = n-1, yn
= yn-1
+ ∆x fn-1

13. • The first derivative provides a direct estimate of the
slope at xi
where f(xi,yi) is the differential equation evaluated at xi
and yi. This estimate can be substituted into the
equation:
• A new value of y is predicted using the slope to
extrapolate linearly over the step size h.
),( ii yxf=φ
hyxfyy iiii ),(1 +=+

14. 1,0
5.820122),(
00
23
==
+−+−==
yxpointStarting
xxxyxf
dx
dy
25.55.0*5.81),(1 =+=+=+ hyxfyy iiii

15. Error Analysis for Euler’s Method/
• Numerical solutions of ODEs involves two types of
error:
– Truncation error
• Local truncation error
• Propagated truncation error
– The sum of the two is the total or global truncation error
– Round-off errors
)(
!2
),(
2
2
hOE
h
yxf
E
a
ii
a
=
′
=

16. Example 3:
Find y(0.5) if y is the solution of IVP y' = -2x-y, y(0) = -1 using
Euler's method with step length 0.1. Also find the error in the
approximation.
Solution:
f(x, y) = -2x - y,
y1 = y0 + h f(x0, y0) = -1 + 0.1* (-2*0 - (-1)) = -0.8999
y2 = y1 + h f(x1, y1) = -0.8999 + 0.1* (-2*0 - (-0.8999)) = -0.8299
y3 = y2 + h f(x2, y2) = -0.8299 + 0.1* (-2*0 - (-0.8299)) = -0.7869
y4 = y3 + h f(x3, y3) = -0.7869 + 0.1* (-2*0 - (-0.7869)) = -0.7683
y5 = y4 + h f(x4, y4) = -0.7683 + 0.1* (-2*0 - (-0.7683)) = -0.7715
Truncation error in the approximation = ( h2
/2 ) f''(x), where 0 < x
<0.5
= 0.005 f''(x)

17. Example 4:
Find y(0.8) with h = 0.1 from y' = y - 2x/y, y(0) = 1 using Euler's
method:-
Solution:
f(x, y) = y - 2x/y
y1
= y0
+ h f(x0
, y0
) = 1.0 + 0.1* ( 1.0- 2*0.0/1.0 ) = 1.1000
y2
= y1
+ h f(x1
, y1
) = 1.1 + 0.1* ( 1.1- 2*0.1/1.1 ) = 1.1918
y3
= y2
+ h f(x2
, y2
) = 1.1918 + 0.1* ( 1.1918- 2*0.2/1.1918 ) = 1.2774
y4
= y3
+ h f(x3
, y3
) = 1.2774 + 0.1* ( 1.2774- 2*0.3/1.2774 ) = 1.3582
y5
= y4
+ h f(x4
, y4
) = 1.3582 + 0.1* ( 1.3582- 2*0.4/1.3582 ) = 1.4351
y6
= y5
+ h f(x5
, y5
) = 1.4351 + 0.1* ( 1.4351- 2*0.5/1.4351 ) = 1.5089
y7
= y6
+ h f(x6
, y6
) = 1.5089 + 0.1* ( 1.5089- 2*0.6/1.5089 ) = 1.5803
y8
= y7
+ h f(x7
, y7
) = 1.5803 + 0.1* ( 1.5803- 2*0.7/1.5803 ) = 1.6497

18. Modified Euler's Method :
The Euler forward scheme may be very easy to implement but it
can't give accurate solutions. A very small step size is required
for any meaningful result. In this scheme, since, the starting point
of each sub-interval is used to find the slope of the solution
curve, the solution would be correct only if the function is linear.
So an improvement over this is to take the arithmetic average of
the slopes at xi
and xi+1
(that is, at the end points of each sub-
interval). The scheme so obtained is called modified Euler's
method. It works first by approximating a value to yi+1
and then
improving it by making use of average slope.
If Euler's method is used to find the first approximation of yi+1
then
yi+1
= yi
+ 0.5h(fi
+ f(xi+1
, yi
+ hfi
))

19. Truncation error:
yi+1 = yi + h y'i + h2
yi'' /2 + h3
yi''' /3! + h4
yi
iv
/4! + . . .
fi+1 = y'i+1 = y'i + h y''i + h2
yi'''' /2 + h3
yi
iv
/3! + h4
yi
v
/4! + . . .
By substituting these expansions in the Modified Euler formula gives
yi + h y'i + h2
yi'' /2 + h3
yi''' /3! + h4
yi
iv
/4! + . . . = yi+ h/2 (y'i + y'i + h y''i
+ h2
yi'''' /2 + h3
yi
iv
/3! + h4
yi
v
/4! + . . . )
So the truncation error is: - h3
yi''' /12 - h4
yi
iv
/24 + . . . that is, Modified
Euler's method is of order two.

20. Example 5:
Find y(1.0) accurate upto four decimal places using Modified Euler's
method by solving the IVP y' = -2xy2
, y(0) = 1 with step lengh 0.2.
Solution:
f(x, y) = -2xy2
y' = -2*x*y*y, y[0.0] = 1.0 with h = 0.2
Given
y[0.0] = 1.0
Euler Solution: y(1) = y(0) + h*(-2*x*y*y)(1)
y[0.20] = 1.0
Modified Euler iterations:y(1) = y(0) + .5*h*((-2*x*y*y)(0) + (-2*x*y*y)(1)
y[0.20] = 1.0 y[0.20] = 0.9599999988079071 y[0.20] =
0.9631359989929199
y[0.20] = 0.9628947607919341 y[0.20] = 0.9629133460803093
Euler Solution: y(2) = y(1) + h*(-2*x*y*y)(2)
y[0.40] = 0.8887359638083165
Modified Euler iterations:y(2) = y(1) + .5*h*((-2*x*y*y)(1) + (-2*x*y*y)(2)
y[0.40] = 0.8887359638083165 y[0.40] = 0.8626358081578545
y[0.40] = 0.8662926943348495 y[0.40] = 0.8657868947404332
y[0.40] = 0.865856981554814

21. Euler Solution: y(3) = y(2) + h*(-2*x*y*y)(3)
y[0.60] = 0.7458966289094106
Modified Euler iterations:y(3) = y(2) + .5*h*((-2*x*y*y)(2) + (-2*x*y*y)(3)
y[0.60] = 0.7458966289094106 y[0.60] = 0.7391085349039348
y[0.60] = 0.7403181774980547 y[0.60] = 0.7401034281837107
y[0.60] = 0.7401415785278189
Euler Solution: y(4) = y(3) + h*(-2*x*y*y)(4)
y[0.80] = 0.6086629119889084
Modified Euler iterations:y(4) = y(3) + .5*h*((-2*x*y*y)(3) + (-2*x*y*y)(4)
y[0.80] = 0.6086629119889084 y[0.80] = 0.6151235687114084
y[0.80] = 0.6138585343771569 y[0.80] = 0.6141072871136244
y[0.80] = 0.6140584135348263
Euler Solution: y(5) = y(4) + h*(-2*x*y*y)(5)
y[1.00] = 0.49340256427369866
Modified Euler iterations:y(5) = y(4) + .5*h*((-2*x*y*y)(4) + (-2*x*y*y)(5)
y[1.00] = 0.49340256427369866 y[1.00] = 0.5050460713552334
y[1.00] = 0.5027209825340415 y[1.00] = 0.5031896121302805
y[1.00] = 0.5030953322323046 y[1.00] = 0.503114306721248

22. 22
Runge-Kutta Methods (RK)
• Runge-Kutta methods achieve the accuracy of a
Taylor series approach without requiring the
calculation of higher derivatives.
),(
),(
),(
),(
constants'
),,(
11,122,1111
22212133
11112
1
2211
1
hkqhkqhkqyhpxfk
hkqhkqyhpxfk
hkqyhpxfk
yxfk
sa
kakaka
hhyxyy
nnnnninin
ii
ii
ii
nn
iiii
−−−−−−
+
+++++=
+++=
++=
=
=
+++=
+=


φ
φ
Increment function
p’s and q’s are constants

23. •RK method of order 2nd
Order (v = 2)
K1 = h f(xi, yi)
K2 = h f(xi + h, yi + K1 )
yi+1 = yi + (K1 + K2 )/2 at xi+1 = xi + h
•RK method of order 4th
Order (v = 4)
K1 = h f(xi, yi)
K2 = h f(xi + h/2, yi + K1 /2)
K3 = h f(xi + h/2, yi + K2 /2)
K4 = h f(xi + h, yi + K3 )
yi+1 = yi + ( K1 + 2K2 + 2K3 + K4 )/6 at at xi+1 = xi + h

24. Example 6:
Using RK method of order four find y at x = 1.1 and 1.2 by solving y' = x2
+
y2
, y(1) = 2.3
Solution: Using RK method of order 4
Given y' = x*x+y*y,
y[1.00] = 2.3
with step-length = 0.1
K1 = 0.628999987438321
K2 = 0.7938110087671021
K3 = 0.83757991687511
K4 = 1.1054407603556848
y[1.10] = 3.1328703854960227
K1 = 1.102487701987972
K2 = 1.4895197934605002
K3 = 1.6358516854539997
K4 = 2.4180710557439085
y[1.20] = 4.761420671422837