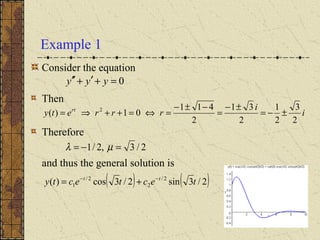
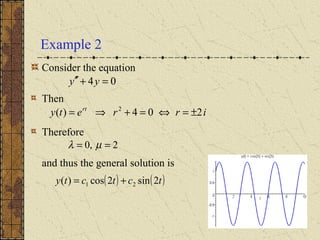
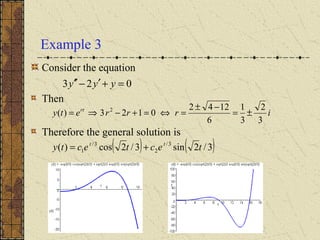
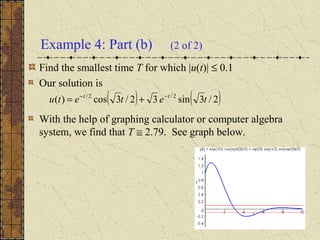
The document discusses complex roots of the characteristic equation arising from assuming exponential solutions to a differential equation. It shows that complex roots lead to complex-valued solutions, but linear combinations of solutions can give real-valued solutions in the form of sine and cosine functions. Several examples are worked out to find the general solution of differential equations and determine the time for the solution to drop below a given value based on its graph.

1. Ch 3.4:
Complex Roots of Characteristic Equation
Recall our discussion of the equation
where a, b and c are constants.
Assuming an exponential soln leads to characteristic equation:
Quadratic formula (or factoring) yields two solutions, r1 & r2:
If b2
– 4ac < 0, then complex roots: r1 = λ + iµ, r2 = λ - iµ
Thus
0=+′+′′ cyybya
0)( 2
=++⇒= cbrarety rt
a
acbb
r
2
42
−±−
=
( ) ( )titi
etyety µλµλ −+
== )(,)( 21

2. Euler’s Formula; Complex Valued Solutions
Substituting it into Taylor series for et
, we obtain Euler’s
formula:
Generalizing Euler’s formula, we obtain
Then
Therefore
( ) ( )
tit
n
t
i
n
t
n
it
e
n
nn
n
nn
n
n
it
sincos
!12
)1(
!2
)1(
!
)(
1
121
0
2
0
+=
−
−
+
−
== ∑∑∑
∞
=
−−∞
=
∞
=
tite ti
µµµ
sincos +=
( )
[ ] tietetiteeee ttttitti
µµµµ λλλµλµλ
sincossincos +=+==+
( )
( )
tieteety
tieteety
ttti
ttti
µµ
µµ
λλµλ
λλµλ
sincos)(
sincos)(
2
1
−==
+==
−
+

3. Real Valued Solutions
Our two solutions thus far are complex-valued functions:
We would prefer to have real-valued solutions, since our
differential equation has real coefficients.
To achieve this, recall that linear combinations of solutions
are themselves solutions:
Ignoring constants, we obtain the two solutions
tietety
tietety
tt
tt
µµ
µµ
λλ
λλ
sincos)(
sincos)(
2
1
−=
+=
tietyty
tetyty
t
t
µ
µ
λ
λ
sin2)()(
cos2)()(
21
21
=−
=+
tetytety tt
µµ λλ
sin)(,cos)( 43 ==

4. Real Valued Solutions: The Wronskian
Thus we have the following real-valued functions:
Checking the Wronskian, we obtain
Thus y3 and y4 form a fundamental solution set for our ODE,
and the general solution can be expressed as
tetytety tt
µµ λλ
sin)(,cos)( 43 ==
( ) ( )
0
cossinsincos
sincos
2
≠=
+−
=
t
tt
tt
e
ttette
tete
W
λ
λλ
λλ
µ
µµµλµµµλ
µµ
tectecty tt
µµ λλ
sincos)( 21 +=

5. Example 1
Consider the equation
Then
Therefore
and thus the general solution is
( ) ( )2/3sin2/3cos)( 2/
2
2/
1 tectecty tt −−
+=
0=+′+′′ yyy
i
i
rrrety rt
2
3
2
1
2
31
2
411
01)( 2
±−=
±−
=
−±−
=⇔=++⇒=
2/3,2/1 =−= µλ

6. Example 2
Consider the equation
Then
Therefore
and thus the general solution is
04 =+′′ yy
irrety rt
204)( 2
±=⇔=+⇒=
2,0 == µλ
( ) ( )tctcty 2sin2cos)( 21 +=

7. Example 3
Consider the equation
Then
Therefore the general solution is
023 =+′−′′ yyy
irrrety rt
3
2
3
1
6
1242
0123)( 2
±=
−±
=⇔=+−⇒=
( ) ( )3/2sin3/2cos)( 3/
2
3/
1 tectecty tt
+=

8. Example 4: Part (a) (1 of 2)
For the initial value problem below, find (a) the solution u(t)
and (b) the smallest time T for which |u(t)| ≤ 0.1
We know from Example 1 that the general solution is
Using the initial conditions, we obtain
Thus
( ) ( )2/3sin2/3cos)( 2/
2
2/
1 tectectu tt −−
+=
1)0(,1)0(,0 =′==+′+′′ yyyyy
3
3
3
,1
1
2
3
2
1
1
21
21
1
===⇒





=+−
=
cc
cc
c
( ) ( )2/3sin32/3cos)( 2/2/
tetetu tt −−
+=

9. Example 4: Part (b) (2 of 2)
Find the smallest time T for which |u(t)| ≤ 0.1
Our solution is
With the help of graphing calculator or computer algebra
system, we find that T ≅ 2.79. See graph below.
( ) ( )2/3sin32/3cos)( 2/2/
tetetu tt −−
+=

10. Example 4: Part (b) (2 of 2)
Find the smallest time T for which |u(t)| ≤ 0.1
Our solution is
With the help of graphing calculator or computer algebra
system, we find that T ≅ 2.79. See graph below.
( ) ( )2/3sin32/3cos)( 2/2/
tetetu tt −−
+=