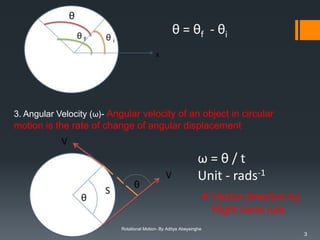
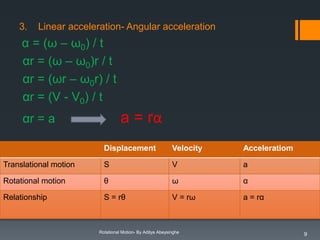
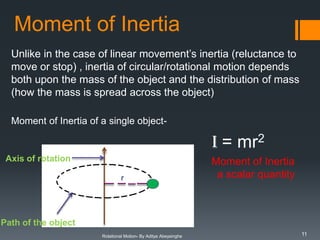
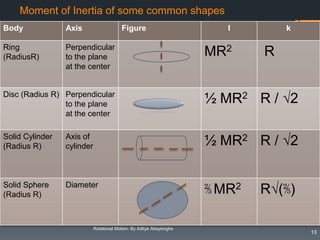
1. The document defines key terms related to rotational motion such as angular position, angular displacement, angular velocity, and angular acceleration. 2. It also outlines the four fundamental equations of angular motion and how they are analogous to the linear equations of motion. 3. Key concepts such as moment of inertia, torque, angular momentum, and their relationships to linear motion are summarized.

1. Rotational Motion
Rotational Motion- By Aditya Abeysinghe
1

2. Definitions of some special terms
1.
Angular position (Φ) - The angular position of a particle is the
angle ɸ made between the line connecting the particle to the
original and the positive direction of the x-axis, measured in a
counterclockwise direction
ɸ=l/r
2. Angular displacement (θ) - The radian value of the angle
displaced by an object on the center of its path in circular motion
from the initial position to the final position is called the angular
displacement.
Rotational Motion- By Aditya Abeysinghe
2

3. θ = θf - θi
3. Angular Velocity (ω)- Angular velocity of an object in circular
motion is the rate of change of angular displacement
ω=θ/t
Unit - rads-1
 Vector direction by
Right hand rule
Rotational Motion- By Aditya Abeysinghe
3

4. 4. Angular acceleration- Angular acceleration of an object in
circular motion is the rate of change of angular velocity
ω
t=t
α = (ω – ω0) / t
r
θ
ω0
t=0
Rotational Motion- By Aditya Abeysinghe
Unit- rads-2
Direction- By right
hand rule
4

5. Angular equations of movement
α = (ω – ω0) / t
ω = ω0 + αt
(ω + ω0 )/2 = θ / t
θ = (ω + ω0 )t/2
(ω + ω0 )/2 = θ / t , ωt = 2θ + ω0t ,
(ω0 + αt)t = 2θ + ω0t
θ = ω0t + ½ αt2
θ = (ω + ω0 )t/2, θ = (ω + ω0 )(ω - ω0 )
2
α
ω2 = ω02 + 2αθ
Rotational Motion- By Aditya Abeysinghe
5

6. Therefore the four equations of angular movement are-
1.
2.
3.
4.
ω = ω0 + αt
θ = (ω + ω0 )t/2
θ = ω0t + ½ αt2
ω2 = ω02 + 2αθ
It should be noted that these four equations are
analogous to the four linear equations of motion:
1. V = U + at
2. S = (V + U)t/2
3. S = Ut + ½ at2
4. V2 = U2 + 2as
Rotational Motion- By Aditya Abeysinghe
6

7. Right hand rule
Take your right hand and curl your fingers along the direction of the
rotation. Your thumb directs along the specific vector you need.
(angular velocity, angular acceleration, angular momentum etc.)
Thus, right hand rule
is used whenever, in
rotational motion, to
measure the
direction of a
particular vector
Direction of
rotation
Axis of rotation
Rotational Motion- By Aditya Abeysinghe
7

8. Relationship between physical
quantities measured in angular
motion and that in linear motion
1.
Linear displacement- Angular displacement
S
r
θ
S= (2πr / 2π ) × θ = rθ
S = rθ
2. Linear velocity- Angular velocity
S/t=rθ/t
V = rω
Rotational Motion- By Aditya Abeysinghe
8

9. 3.
Linear acceleration- Angular acceleration
α = (ω – ω0) / t
αr = (ω – ω0)r / t
αr = (ωr – ω0r) / t
αr = (V - V0) / t
a = rα
αr = a
Displacement
Velocity
Acceleratiom
Translational motion
S
V
a
Rotational motion
θ
ω
α
Relationship
S = rθ
V = rω
a = rα
Rotational Motion- By Aditya Abeysinghe
9

10. The period and the frequency
of an object in rotation motion
Period (T) is the time taken by an object in
rotational motion to complete one complete
circle.
Frequency (f) is the no. of cycles an object
rotates around its axis of rotation
Thus, f = 1/ T . However, ω = θ / t
Therefore, ω = 2π / T
Therefore, ω = 2π / (1/f)
Thus, ω = 2πf
Rotational Motion- By Aditya Abeysinghe
10

11. Moment of Inertia
Unlike in the case of linear movement’s inertia (reluctance to
move or stop) , inertia of circular/rotational motion depends
both upon the mass of the object and the distribution of mass
(how the mass is spread across the object)
Moment of Inertia of a single object-
I = mr2
Axis of rotation
is
r
Moment of Inertia
a scalar quantity
m
Path of the object
Rotational Motion- By Aditya Abeysinghe
11

12. Radius of gyration
Suppose a body of mass M has moment of Inertia I
about an axis. The radius of gyration, k, of the body
about the axis is defined as
I= Mk2
That is k is the distance of a point mass M
from the axis of rotation such that this point
mass has the same moment of inertia about
the axis as the given body.
Rotational Motion- By Aditya Abeysinghe
12

13. Moment of Inertia of some common shapes
Body
Axis
Figure
Ring
(RadiusR)
Perpendicular
to the plane
at the center
I
MR2
k
R
Disc (Radius R) Perpendicular
to the plane
at the center
½ MR2 R / √2
Solid Cylinder
(Radius R)
Axis of
cylinder
½ MR2 R / √2
Solid Sphere
(Radius R)
Diameter
⅖ MR2
Rotational Motion- By Aditya Abeysinghe
R√(⅖)
13

14. Angular Momentum
Angular momentum is the product of the moment of inertia and the
angular velocity of the object.
z
L = r sin θ × P
L = r P Sinθ
y
r
P
θ
x
L= Iω Sinθ
However, P= mv ,
(Linear moment= mass × linear velocity )
Therefore, L= m r v Sinθ
= m r (ω r ) Sinθ (as V= rω)
= mr2 ω Sinθ
Therefore, L = Iω Sin θ (as I = mr2)
Rotational Motion- By Aditya Abeysinghe
14

15. But in most cases the radius of rotation is perpendicular to the
momentum.
Thus, θ = 90° ,
L = Iω
P
r
Axis of
rotation
Rotational Motion- By Aditya Abeysinghe
15

16. Torque
The rate of change of angular momentum of an
object in rotational motion is proportional to the
external unbalanced torque. The direction of
the torque also lies in the direction of the
angular momentum.
Torque is called the moment of force and is a
measure of the turning effect of the force about
a given axis.
A torque is needed to rotate an object at rest or
to change the rotational mode of an object.
Rotational Motion- By Aditya Abeysinghe
16

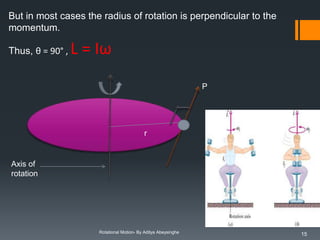
17. τ = (Iω – Iω0 )/t
τ = I [(ω - ω0 )/t]
Therefore,
τ = Iα
By Newton’s second law
of motion
F = ma
Fr = mra = mr (rα) ( as
a=rα)
Fr= mr2 α
Fr = Iα
( as I= mr2 )
However, from the above
derivation, Iα = τ .
Therefore, Fr = τ
Thus
, τ = Fr
Rotational Motion- By Aditya Abeysinghe
17

18. This theory can be expressed as:
z
F
θ
r
O
y
d
τ = F×r
x
Rotational Motion- By Aditya Abeysinghe
τ = Fd
τ = Fr Sinθ
18

19. Relationship between Torque and Angular
Momentum-
τ = dL / dt
τ – Net torque
L- Angular momentum
This result is the rotational analogue of
Newton’s second law:
F = dP / dt
Rotational Motion- By Aditya Abeysinghe
19

20. Applying Newton’s laws to
rotational motion
1. Newton’s First law and equilibriumIf the net torque acting on a rigid object is zero, it will
rotate with a constant angular velocity.
If the system
Concept of equilibriumd
M
Therefore, τM
3d
m
O
is
at
equilibrium, total
torque around O
should be zero
+ τm = 0
Mgd + [ -(mg(3d))] = 0
Therefore, m = M/3
Rotational Motion- By Aditya Abeysinghe
20

21. 2. Newton’s second law of motion
The rate of change of angular momentum of an object in rotational
motion is proportional to the external unbalanced torque. The direction
of the torque also lies in the direction of the angular momentum.
τ α α
τ = Iα
This is analogous to the linear equivalent, which states,
The rate of change of momentum is directly proportional to the
external unbalanced force applied on an object and that force lies
in the direction of the net momentum.
Thus, torque could be treated as the rotational
analogue of the force applied on an object.
Rotational Motion- By Aditya Abeysinghe
21

22. Theorem of Parallel Axes
Let ICM be the moment of inertia of a body of mass M about an
axis passing through the center of mass and let I be the moment
of inertia about a parallel axis at a distance d from the first axis.
Then, I = ICM + Md2
Thus the minimum
moment of inertia
for any object is at
the center of
mass, as x in the
above expression
is zero.
Rotational Motion- By Aditya Abeysinghe
22

23. Theorem of perpendicular axis
The moment of inertia of a body about an axis perpendicular to its
plane is equal to the sum of moments of inertia about two mutually
perpendicular axis in its own plane and crossing through the point
through which the perpendicular axis passes
Iz = Ix + Iy
Rotational Motion- By Aditya Abeysinghe
23

24. Rotational Kinetic Energy
ω
mn
rn
r1
r2
Ek = Σ ½ mi vi2
But, vi = riω
So, Ek = Σ ½ mi ri2ω2
= ½ (Σ mi ri2 ) ω2
Therefore, Ek = ½ I ω2
m1
m2
Ek = ½ I
2
ω
Rotational kinetic energy is the rotational analogue of the translational kinetic
energy, which is EK = ½ mv2. In fact, rotational kinetic energy equation can
be deduced by substituting v =rω and viceversa.
Rotational Motion- By Aditya Abeysinghe
24

25. Law of Conservation of Angular
Momentum
Law- If the resultant external torque on a system is
zero, its total angular momentum remains constant.
That is, if τ = 0, dL / dt = 0 , which means that L is a constant
This is the rotational analogue of the law of conservation of linear
momentum.
Rotational Motion- By Aditya Abeysinghe
25

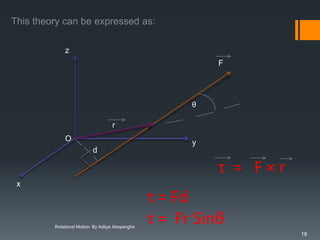
26. Work done by a torque
dW = τ dθ
Therefore, the total work done in rotating the body from an angular
displacement of θ1 to an angle displacement θ2 is
θ2
W=
∫ τ dθ
θ1
θ2
W= τ ∫ 1. dθ
θ1
Therefore,
W= τ [θ2 - θ1 ]
Rotational Motion- By Aditya Abeysinghe
26

27. Power
The rate at which work is done by a torque is called
Power
P= dw/dt = τ dθ/dt = τ ω
Therefore, P
=τω
Rotational Motion- By Aditya Abeysinghe
27

28. Work - Energy Principle
From ω2 = ω02 + 2αθ and W= τθ , it is clear that the work
done by the net torque is equal to the change in
rotational kinetic energy.
τ = Iα and ω2 = ω02 + 2αθ .
Therefore, ω2 = ω02 + 2(τ/I)θ .
Thus, ω2 = ω02 + 2[(τθ)/I] .
Thus, ω2 = ω02 + 2W/I
OR
W= ½ I (ω2 - ω02 ). This is called
the work-energy principle.
Rotational Motion- By Aditya Abeysinghe
28

29. Relationship between Angular
momentum and Angular velocity
τ = Iα = I dω/dt = d(Iω)/dt
But, τ = dL/dt
Thus, dL/dt = d(Iω)/dt
By integrating both sides,
It can be shown that,
L = Iω
This is the rotational analogue of P = mv
Rotational Motion- By Aditya Abeysinghe
29

30. Rolling Body
Rolling is a combination of rotational and transitional(linear)
motions.
Suppose a sphere is rolling on a plane surface, the velocity
distribution can be expressed as,
Rotational Motion- By Aditya Abeysinghe
30

31. This two systems (rotational and transitional) can
be combined together to understand how actually
the sphere above moves in the plane. The final
distribution shows clearly that in reality the ball
always instantly experiences a zero velocity at the
point of contact with the surface and the maximum
velocity is at the top
2V
V
V √2
V
Rotational Motion- By Aditya Abeysinghe
V=0
31

32. Thus, Etotal = Etransitional + Erotational
E=½
2
mv
+ ½
2
Iω
E = ½ mR2 ω2 + ½ mk2 ω2
(Where k- radius of gyration)
E=
2
½mω
2
(R
+
2)
k
Rotational Motion- By Aditya Abeysinghe
32

33. A body rolling down an inclined
plane
From the conservation of energy,
Mgh = ½mv2 + ½Iω2
s
h
mg
θ
Rotational Motion- By Aditya Abeysinghe
33

34. Equilibrium of a rigid body
1.
Transitional Equilibrium
For a body to be in transitional equilibrium, the vector sum
of all the external forces on the body must be zero.
Fext = M acm
and acm must be zero for transitional equilibrium.
2. Rotational Equilibrium
For a body to be in rotational equilibrium, the vector sum of
all the external torques on the body about any axis must be
zero.
τext = Iα
and α must be zero for rotational equilibrium.
Rotational Motion- By Aditya Abeysinghe
34

35. Summarizing it up!!
Term
Definition
Angular position
The angular position of a particle is the angle ɸ made between
the line connecting the particle to the original and the positive
direction of the x-axis, measured in a counterclockwise direction
Angular
displacement
The radian value of the angle displaced by an object on the
center of its path in circular motion from the initial position to the
final position is called the angular displacement.
Angular velocity
Angular velocity of an object in circular motion is the rate of
change of angular displacement
Angular acceleration
Angular acceleration of an object in circular motion is the rate of
change of angular velocity
Angular equations of
motion
ω = ω0 + αt , θ = (ω + ω0 )t/2 ,
θ = ω0t + ½ αt2 , ω2 = ω02 + 2αθ
Rotational Motion- By Aditya Abeysinghe
35

36. Right hand rule
Take your right hand and curl your fingers along the direction of the
rotation.Your thumb directs along the specific vector you need
Relationship
between linear
and angular
qualities
S = rθ , V = rω , a = rα
(s- translational displacement , v- translational velocity,
a-translational acceleration )
Period and
frequency
Period (T) is the time taken by an object in circular motion to complete
one complete circle.
Frequency (f) is the no. of cycles an object rotates around its axis of
rotation
Thus, f = 1/ T
Moment of
inertia
Inertia of circular/rotational motion depends both upon the mass of the
object and the distribution of mass.
Radius of
gyration
The radius of gyration, k, of the body about the axis is defined as
I= Mk2
Angular
momentum
Angular momentum is the product of the moment of inertia and the
angular velocity of the object.
Rotational Motion- By Aditya Abeysinghe
36

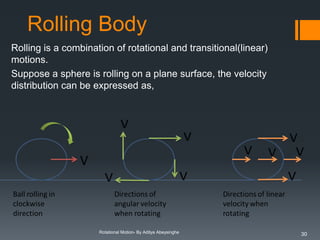
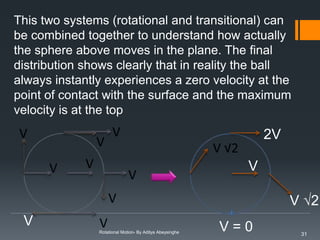
37. Torque
Torque is called the moment of force and is a measure of the
turning effect of the force about a given axis.
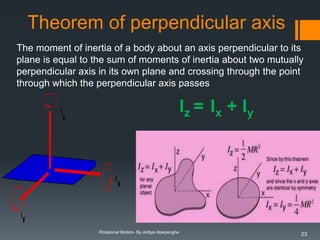
Theorem of parallel
axes
Let ICM be the moment of inertia of a body of mass M about an
axis passing through the center of mass and let I be the moment
of inertia about a parallel axis at a distance d from the first axis.
Then, I = ICM + Md2
Theorem of
perpendicular axes
The moment of inertia of a body about an axis perpendicular to its
plane is equal to the sum of moments of inertia about two
mutually perpendicular axis in its own plane and crossing through
the point through which the perpendicular axis passes
Iz = Ix + I y
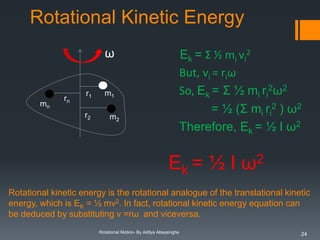
Rotational kinetic
energy
Ek = ½ I ω2
Law of conservation
of angular
momentum
If the resultant external torque on a system is zero, its total
angular momentum remains constant.
Work done
W = τ [θ2 - θ1 ]

38. Power
The rate at which work is done by a torque is called
Power
P=τω
Work-Energy principle
W= ½ I (ω2 - ω02 ). This is called the work-energy
principle.
Rolling body
Rolling is a combination of rotational and
transitional(linear) motions.
Equilibrium of a rigid body
1.
Transitional Equilibrium
For a body to be in transitional equilibrium, the vector
sum of all the external forces on the body must be zero.
Fext = Macm
and acm must be zero for transitional equilibrium.
2. Rotational Equilibrium
For a body to be in rotational equilibrium, the vector
sum of all the external torques on the body about any axis
must be zero.
τ = Iα and α must be zero for rotational equilibrium.