The document discusses complex differentiability and analytic functions. It shows that for a function f(z) to be complex differentiable, the Cauchy-Riemann equations relating the partial derivatives of the real and imaginary parts must be satisfied. It also discusses representing functions as power series and their radii of convergence. Multivalued functions like logarithms and roots are discussed, noting the need for branch cuts to define single-valued branches.

1. f ( z ) = u( x , y ) + iv ( x , y ) for z = x + iy
f ( z + ∆z ) − f ( z )
f ' ( z ) = lim [ ] exists
∆z →0 ∆z
Its value does not depend on the direction.
Ex : Show that the function f ( z ) = x 2 − y 2 + i 2 xy is
differentiable for all values of z .
for ∆z = ∆x + i∆y
f ( z + ∆z ) − f ( z )
f ' ( z ) = lim
∆z →0 ∆z
( x + ∆x ) 2 − ( y + ∆y ) 2 + 2i ( x + ∆x )( y + ∆y ) − x 2 + y 2 − 2ixy
=
∆x + i∆y
( ∆x ) 2 − ( ∆y )2 + 2i∆x∆y
= 2x + i2 y +
∆x + i∆y
(1) choose ∆y = 0, ∆x → 0 ⇒ f ' ( z ) = 2 x + i 2 y
(2) choose ∆x = 0, ∆y → 0 ⇒ f ' ( z ) = 2 x + i 2 y

2. * * Another method :
f ( z ) = ( x + iy ) 2 = z 2
' ( z + ∆z )2 − z 2 ( ∆z )2 + 2 z∆z
f ( z ) = lim [ ] = lim [ ]
∆z →0 ∆z ∆z → 0 ∆z
= lim ∆z + 2 z = 2 z
∆z → 0
Ex : Show that the function f ( z ) = 2 y + ix is not
differentiable anywhere in the complex plane.
f ( z + ∆z ) − f ( z ) 2 y + 2∆y + ix + i∆x − 2 y − ix 2∆y + i∆x
= =
∆z ∆x + i∆y ∆x + i∆y
if ∆z → 0 along a line thriugh z of slope m ⇒ ∆y = m ∆x
f ( z + ∆z ) − f ( z ) 2 ∆ y + i∆ x 2m + i
f ' ( z ) = lim = lim [ ]=
∆z →0 ∆z ∆x ,∆y →0 ∆x + i∆y 1 + im
The limit depends on m (the direction), so f ( z )
is nowhere differentiable.

3. Ex : Show that the function f ( z ) = 1 /(1 − z ) is analytic everywhere
except at z = 1.
f ( z + ∆z ) − f ( z ) 1 1 1
f ' ( z ) = lim [ ] = lim [ ( − )]
∆z →0 ∆z ∆z →0 ∆z 1 − z − ∆z 1 − z
1 1
= lim [ ]=
∆z →0 (1 − z − ∆z )(1 − z ) (1 − z ) 2
Provided z ≠ 1, f ( z ) is analytic everywhere such that
f ' ( z ) is independent of the direction.

4. 20.2 Cauchy-Riemann relation
A function f(z)=u(x,y)+iv(x,y) is differentiable and analytic,
there must be particular connection between u(x,y) and v(x,y)
f ( z + ∆z ) − f ( z )
L = lim [ ]
∆z →0 ∆z
f ( z ) = u( x , y ) + iv ( x , y ) ∆z = ∆x + i∆y
f ( z + ∆z ) = u( x + ∆x , y + ∆y ) + iv ( x + ∆x , y + ∆y )
u( x + ∆x , y + ∆y ) + iv ( x + ∆x , y + ∆y ) − u( x , y ) − iv ( x , y )
⇒ L = lim [ ]
∆x ,∆y →0 ∆x + i∆y
(1) if suppose ∆z is real ⇒ ∆y = 0
u( x + ∆x , y ) − u( x , y ) v ( x + ∆x , y ) − v ( x , y ) ∂u ∂v
⇒ L = lim [ +i ]= +i
∆x →0 ∆x ∆x ∂x ∂x
(2) if suppose ∆z is imaginary ⇒ ∆x = 0
u( x , y + ∆y ) − u( x , y ) v ( x , y + ∆y ) − v ( x , y ) ∂u ∂v
⇒ L = lim [ +i ] = −i +
∆y →0 i ∆y i ∆y ∂y ∂y
∂u ∂v ∂v ∂u
= and =- Cauchy - Riemann relations
∂x ∂y ∂x ∂y

5. Ex : In which domain of the complex plane is
f ( z ) =| x | − i | y | an analytic function?
u( x , y ) =| x |, v ( x , y ) = − | y |
∂u ∂v ∂ ∂
(1) = ⇒ | x |= [− | y |] ⇒ (a) x > 0, y < 0 the fouth quatrant
∂x ∂y ∂x ∂y
(b) x < 0, y > 0 the second quatrant
∂v ∂u ∂ ∂
(2) =− ⇒ [− | y |] = − | x |
∂x ∂y ∂x ∂y
z = x + iy and complex conjugate of z is z * = x − iy
⇒ x = ( z + z * ) / 2 and y = ( z − z * ) / 2i
∂f ∂f ∂x ∂f ∂y 1 ∂u ∂v i ∂v ∂u
⇒ = + = ( − )+ ( + )
∂z * ∂x ∂z * ∂y ∂z * 2 ∂x ∂y 2 ∂x ∂y
If f ( z ) is analytic , then the Cauchy - Riemann relations
are satisfied. ⇒ ∂f / ∂z * = 0 implies an analytic fonction of z contains
the combination of x + iy , not x − iy

6. If Cauchy - Riemann relations are satisfied
∂ ∂u ∂ ∂v ∂ ∂v ∂ ∂u ∂ 2u ∂ 2u
(1) ( ) = ( )= ( ) = − ( )⇒ 2 + 2 2 = 0
∂x ∂x ∂x ∂y ∂y ∂x ∂y ∂y ∂x ∂ y
∂ 2v ∂ 2v
(2) the same result for function v ( x , y ) ⇒ 2
+ 2 2
=0
∂x ∂ y
⇒ u( x , y ) and v ( x , y ) are solutions of Laplace' s
equation in two dimension.
For two families of curves u( x , y ) = conctant and v ( x , y ) = constant,
the normal vectors corresponding the two curves, respectively, are
 ∂u ˆ ∂u ˆ  ∂v ˆ ∂v ˆ
∇u( x , y ) = i+ j and ∇v ( x , y ) = i+ j
∂x ∂y ∂x ∂y
  ∂u ∂v ∂u ∂v ∂u ∂u ∂u ∂u
∇u ⋅ ∇v = + =− + = 0 orthogonal
∂x ∂x ∂y ∂y ∂x ∂y ∂y ∂x

7. 20.3 Power series in a complex variable
∞ ∞
f (z) = ∑ an z n
= ∑ an r n exp(inθ )
n= 0 n=0
∞
if ∑ | an | r n is convergent ⇒ f ( z ) is absolutely convergent
n=0
∞
Is ∑ | a n | r n convergent or not, can be justisfied by" Cauchy root test".
n= 0
1
The radius of convergence R ⇒ = lim | a n |1 / n ⇒ (1) | z |< R absolutely convergent
R n→ ∞
(2) | z |> R divergent
(3) | z |= R undetermined
∞
zn 1
(1) ∑ ⇒ lim ( )1 / n = 0 ⇒ R = ∞ converges for all z
n= 0 n! n→∞ n!
∞
(2) ∑ n! z n ⇒ lim ( n! )1 / n = ∞ ⇒ R = 0 converges only at z = 0
n= 0 n →∞

8. 20.4 Some elementary functions
∞
zn
Define exp z = ∑
n = 0 n!
Ex : Show that exp z1 exp z 2 = exp( z1 + z 2 )
∞
( z1 + z 2 ) n
exp( z1 + z 2 ) = ∑
n=0 n!
∞
1 n n
= ∑ n!(C 0 z1 + C1n z1n−1 z2 + C 2 z1n−2 z2 + C rn z1n−r z2 + ... + C n z2 )
n 2 r n n
n= 0
n
s r Cr 1 n! 1
set n = r + s ⇒ the coeff. of z1 z 2 is = =
n! n! ( n − r )! r ! s! r !
∞
zs ∞ zr ∞ ∞
1 s r
exp z1 exp z 2 = ∑ ∑ = ∑∑ z1 z 2
s =0 s! r = 0 r ! s =0 r = 0 s! r !
s r
There are the same coeff. of z1 z 2 for the above two terms.

9. Define the complex comonent of a real number a > 0
∞
z n (ln a ) n
a = exp( z ln a ) = ∑
z
n=0 n!
(1) if a = e ⇒ e z = exp( z ln e ) = exp z the same as real number
iy y 2 iy 3
(2) if a = e, z = iy ⇒ e = exp(iy ) = 1 − − + ...
2! 3!
y2 y4 y3
= 1− + + ..... + i ( y − + ...) = cos y + i sin y
2! 4! 3!
(3) if a = e , z = x + iy ⇒ e x + iy = e x e iy = exp( x )(cos y + i sin y )

10. Set exp w = z
Write z = r exp iθ for r is real and − π < θ ≤ π
⇒ z = r exp[i (θ + 2nπ )] ⇒ w = Lnz = ln r + i (θ + 2nπ )
Lnz is a multivalued function of z .
Take its principal value by choosing n = 0
⇒ ln z = ln r + iθ -π < θ ≤ π
If t ≠ 0 and z are both complex numbers, we define
t z = exp( zLnt )
Ex : Show that there are exactly n distinct nth roots of t .
1
1
tn = exp( Lnt ) and t = r exp[i (θ + 2kπ )]
n
1 1
1 (θ + 2kπ ) (θ + 2kπ )
⇒ tn = exp[ ln r + i ] = r n exp[i ]
n n n

11. 20.5 Multivalued functions and branch cuts
A logarithmic function, a complex power and a complex root are all
multivalued. Is the properties of analytic function still applied?
Ex : f ( z ) = z 1 / 2 and z = r exp(iθ ) (A) C
y
(A) z traverse any closed contour C that
dose not enclose the origin, θ return r
to its original value after one complete θ
x
circuit.
(B) y
(B) θ → θ + 2π enclose the origin
C' r
1/ 2 1/ 2
r exp(iθ / 2) → r exp[i (θ + 2π ) / 2]
θ
= − r 1 / 2 exp(iθ / 2) x
⇒ f (z) → − f (z)
z = 0 is a branch point of the function f ( z ) = z 1 / 2

12. Branch point: z remains unchanged while z traverse a closed contour C
about some point. But a function f(z) changes after one complete circuit.
Branch cut: It is a line (or curve) in the complex plane that we must cross ,
so the function remains single-valued.
y
Ex : f ( z ) = z 1 / 2
restrict θ ⇒ 0 ≤ θ < 2π
⇒ f ( z ) is single - valued 0
x

13. Ex : Find the branch points of f ( z ) = z 2 + 1 , and hence sketch
suitable arrangements of branch cuts.
f ( z ) = z 2 + 1 = ( z + i )( z − i ) expected branch points : z = ± i
set z − i = r1 exp(iθ1 ) and z + i = r2 exp(iθ 2 )
⇒ f ( z ) = r1r2 exp(iθ1 / 2) exp(iθ 2 / 2)
= r1r2 exp[i (θ1 + θ 2 )]
If contour C encloses
(1) neither branch point, then θ1 → θ1 , θ 2 → θ 2 ⇒ f ( z ) → f ( z )
(2) z = i but not z = − i , then θ1 → θ1 + 2π , θ 2 → θ 2 ⇒ f ( z ) → − f ( z )
(3) z = − i but not z = i , then θ1 → θ1 , θ 2 → θ 2 + 2π ⇒ f ( z ) → − f ( z )
(4) both branch points, then θ1 → θ1 + 2π ,θ 2 → θ 2 + 2π ⇒ f ( z ) → f ( z )

14. f ( z ) changes value around loops containing
either z = i or z = − i . We choose branch cut as follows :
(A) y
(B) y
i
i
x x
−i
−i

15. 20.6 Singularities and zeros of complex function
g( z )
Isolated singularity (pole) : f ( z ) =
( z − z0 ) n
n is a positive integer, g( z ) is analytic at all points in
some neighborhood containing z = z0 and g( z0 ) ≠ 0,
the f ( z ) has a pole of order n at z = z0 .
* * An alternate definition for that f ( z ) has a pole of
order n at z = z0 is
lim [( z − z0 ) n f ( z )] = a
z → z0
f ( z ) is analytic and a is a finite, non - zero complex number
(1) if a = 0, then z = z0 is a pole of order less than n.
(2) if a is infinite, then z = z0 is a pole of order greater than n.
(3) if z = z0 is a pole of f ( z ) ⇒| f ( z ) |→ ∞ as z → z0
(4) from any direction, if no finite n satisfies the limit ⇒ essential singularity

16. Ex : Find the singularities of the function
1 1
(1) f ( z ) = −
1− z 1+ z
2z
⇒ f (z) = poles of order 1 at z = 1 and z = −1
(1 − z )(1 + z )
(2) f ( z ) = tanh z
sinh z exp z − exp(− z )
= =
cosh z exp z + exp(− z )
f ( z ) has a singularity when exp z = − exp(− z )
⇒ exp z = exp[i ( 2n + 1)π ] = exp(− z ) n is any integer
1
⇒ 2 z = i ( 2n + 1)π ⇒ z = ( n + )πi
2
Using l' Hospital' s rule
[ z − ( n + 1 / 2)πi ] sinh z [ z − ( n + 1 / 2)πi ] cosh z + sinh z
lim { }= lim { }=1
z →( n+1 / 2 )πi cosh z z →( n+1 / 2 )πi sinh z
each singularity is a simple pole (n = 1)

17. Remove singularties :
Singularity makes the value of f ( z ) undetermined, but lim f ( z )
z→ z0
exists and independent of the direction from which z0 is approached.
Ex : Show that f ( z ) = sin z / z is a removable singularity at z = 0
Sol : lim f ( z ) = 0 / 0 undetermined
z →0
1 z3 z5 z3 z5
f (z) = (z − + − ........) = 1 − + − ....
z 3! 5! 3! 5!
lim f ( z ) = 1 is independent of the way z → 0, so
z →0
f ( z ) has a removable singularity at z = 0.

18. The behavior of f ( z ) at infinity is given by that of
f (1 / ξ ) at ξ = 0, where ξ = 1 / z
Ex : Find the behavior at infinity of (i) f ( z ) = a + bz −2
(ii) f ( z ) = z (1 + z 2 ) and (iii) f ( z ) = exp z
(i) f ( z ) = a + bz − 2 ⇒ set z = 1 / ξ ⇒ f (1 / ξ ) = a + bξ 2
is analytic at ξ = 0 ⇒ f ( z ) is analytic at z = ∞
(ii) f ( z ) = z (1 − z 2 ) ⇒ f (1 / ξ ) = 1 / ξ + 1 / ξ 3 has a pole of
order 3 at z = ∞
∞
(iii) f ( z ) = exp z ⇒ f (1 / ξ ) = ∑ (n! )−1ξ −n
n= 0
f ( z ) has an essential singularity at z = ∞

19. If f ( z0 ) = 0 and f ( z ) = ( z − z0 )n g ( z ), if n is
a positive integer, and g( z0 ) ≠ 0
(i) z = z0 is called a zero of order n.
(ii) if n = 1, z = z0 is called a simple zero.
(iii) z = z0 is also a pole of order n of 1 / f ( z )

20. 20.10 Complex integral y
B
A real continuous parameter t , for α ≤ t ≤ β
C2
x = x ( t ), y = y( t ) and point A is t = α ,
C1
point B is t = β
⇒ ∫ f ( z )dz = ∫ ( u + iv )(dx + idy ) x
C C
A C3
= ∫ udx − ∫ vdy + i ∫ udy + i ∫ vdx
C C C C
β dx β dy β dy β dx
=∫ u dt − ∫ v dt + i ∫ u dt + i ∫ v dt
α dt α dt α dt α dt

21. Ex : Evaluate the complex integral of f ( z ) = 1 / z , along
the circle |z| = R, starting and finishing at z = R. y
z ( t ) = R cos t + iR sin t , 0 ≤ t ≤ 2π C1
dx dy 1 x − iy R
= − R sin t , = R cos t , f ( z ) = = 2 = u + iv , t
dt dt x + iy x + y 2
x
x cos t −y − sin t
u= 2 = ,v = 2 =
x + y2 R x + y2 R
1 2π cos t 2π − sin t
∫C1 z dz = ∫0 R (− R sin t )dt − ∫0 ( R ) R cos tdt
2π cos t 2π − sin t
+ i∫ R cos tdt + i ∫ ( )( − R sin t )dt
0 R 0 R
= 0 + 0 + iπ + iπ = 2πi
* * The integral is also calculated by
dz 2π − R sin t + iR cos t 2π
∫C1 z 0 R cos t + iR sin t
=∫ dt = ∫ idt = 2πi
0
The calculated result is independent of R.

22. Ex : Evaluate the complex integral of f ( z ) = 1 / z along
(i) the contour C 2 consisting of the semicircle | z |= R in
the half - plane y ≥ 0
(ii) the contour C 3 made up of two straight lines C 3a and C 3b
(i) This is just as in the previous example, but for
y
0 ≤ t ≤ π ⇒ ∫ dz / z = πi iR
C2
C 3b
(ii) C 3a : z = (1 − t ) R + itR for 0 ≤ t ≤ 1 C 3a
C 3b : − sR + i (1 − s ) R for 0 ≤ s ≤ 1 s=1 t=0
dz 1 − R + iR 1 − R − iR −R R x
∫C3 z 0 R + t (− R + iR) 0 iR + s(− R − iR)
=∫ dt + ∫ dt
1 −1+ i 1 2t − 1 1 1
1st term ⇒ ∫ dt = ∫ dt + i ∫ dt
0 1 − t + it 0 1 − 2 t + 2t 2 0 1 − 2t + 2t 2
1 i t −1/ 2 1
= [ln(1 − 2t + 2t 2 )] |1 + [2 tan −1 (
0 )] |0
2 2 1/ 2
i π π πi a x
= 0 + [ − ( − )] = ∫ a2 + x2 dx = tan −1 ( ) + c
2 2 2 2 a

23. 1 1+ i 1 (1 + i )[ s − i ( s − 1)]
2nd term ⇒ ∫ ds = ∫ ds
0 s + i ( s − 1) 0 2
s + ( s − 1) 2
1 2s − 1 1 1
=∫ ds + i ∫ ds
0 2s 2 − 2s + 1 0 2s 2 − 2s + 1
1 s −1/ 2 1
= [ln( 2 s 2 − 2 s + 1)] |1 + i tan −1 (
0 ) |0
2 1/ 2
π π πi
= 0 + i[ − ( − )] =
4 4 2
dz
⇒ ∫C3 z = πi
The integral is independent of the different path.

24. Ex : Evaluate the complex integral of f ( z ) = Re( z ) along
the path C1 , C 2 and C 3 as shown in the previous examples.
2π
(i) C1 : ∫ R cos t ( − R sin t + iR cos t )dt = iπR 2
0
π iπ 2
(ii) C 2 : ∫ R cos t ( − R sin t + iR cos t )dt = R
0 2
(iii) C 3 = C 3a + C 3b :
1 1
∫0 (1 − t ) R( − R + iR )dt + ∫ ( − sR )( − R − iR )ds
0
1 1
= R 2 ∫ (1 − t )( −1 + i )dt + R 2 ∫ s(1 + i )ds
0 0
1 2 1
= R ( −1 + i ) + R 2 (1 + i ) = iR 2
2 2
The integral depends on the different path.

25. 20.11 Cauchy theorem
If f ( z ) is an analytic function, and f ' ( z ) is continuous
at each point within and on a closed contour C
⇒ ∫ f ( z )dz = 0
C
∂p( x , y ) ∂q( x , y )
If and are continuous within and
∂x ∂y
on a closed contour C, then by two - demensional
∂p ∂q
divergence theorem ⇒ ∫∫ ( + )dxdy = ∫ ( pdy − qdx )
R ∂x ∂y C
f ( z ) = u + iv and dz = dx + idy
I = ∫ f ( z )dz = ∫ ( udx − vdy ) + i ∫ (vdx + udy )
C C C
∂ ( − u) ∂ ( − v ) ∂ ( − v ) ∂u
= ∫∫ [ + ]dxdy + i ∫∫ [ + ]dxdy = 0
R ∂y ∂x R ∂y ∂x
f ( z ) is analytic and the Cauchy - Riemann relations apply.

26. Ex : Suppose twos points A and B in the complex plane are joined
by two different paths C1 and C 2 . Show that if f ( z ) is an
analytic function on each path and in the region enclosed by the
two paths then the integral of f ( z ) is the same along C1 and C 2 .
y
B
∫C 1
f ( z )dz − ∫
C2
f ( z )dz = ∫
C1 − C 2
f ( z )dz = 0 C1
path C1 − C 2 forms a closed contour enclosing R R
⇒∫ f ( z )dz = ∫ f ( z )dz x
C1 C2
A

27. Ex : Consider two closed contour C and γ in the Argand diagram, γ being
sufficiently small that it lies completely with C . Show that if the function
f ( z ) is analytic in the region between the two contours then ∫ f ( z )dz = ∫ f ( z )dz
C γ
the area is bounded by Γ, and
f ( z ) is analytic C
y
∫Γ f ( z )dz = 0 γ
C1
= ∫ f ( z )dz + ∫ f ( z )dz + ∫ f ( z )dz + ∫ f ( z )dz
C γ C1 C2
If take the direction of contour γ as that of C2
contour C ⇒ ∫ f ( z )dz = ∫ f ( z )dz
C γ
x
Morera' s theorem :
if f ( z ) is a continuous function of z in a closed domain R
bounded by a curve C , for ∫ f ( z )dz = 0 ⇒ f ( z ) is analytic.
C

28. 20.12 Cauchy’s integral formula
If f ( z ) is analytic within and on a closed contour C
1 f (z)
2πi ∫C z − z0
and z0 is a point within C then f ( z0 ) = dz
f (z) f (z) C
I=∫ dz = ∫ dz
C z − z0 γ z−z
0
for z = z0 + ρ exp(iθ ), dz = iρ exp(iθ )dθ γ
2π f ( z0 + ρe iθ ) z0
I=∫ iρe iθ dθ
0 ρe iθ
2π ρ →0
iθ
= i∫ f ( z0 + ρe )dθ = 2πif ( z0 )
0

29. The integral form of the derivative of a complex function :
1 f (z)
f ' ( z0 ) =
2πi ∫C ( z − z )2 dz
0
f ( z 0 + h) − f ( z 0 )
f ' ( z0 ) = lim
h→ 0 h
1 f (z) 1 1
= lim [
h→0 2πi
∫C h z − z0 − h z − z0 )dz ]
( −
1 f (z)
= lim [
h→ 0 2πi ∫C ( z − z0 − h)( z − z0 )dz ]
1 f (z)
=
2πi ∫C ( z − z )2 dz
0
n! f (z)
2πi ∫C ( z − z0 )n+1
For nth derivative f ( n ) ( z0 ) = dz

30. Ex : Suppose that f ( z ) is analytic inside and on a circleC of radius
R centered on the point z = z0 . If | f ( z ) |≤ M on the circle, where
Mn!
M is some constant, show that | f ( n ) ( z0 ) |≤ n
.
R
n! f ( z )dz n! M Mn!
| f ( n ) ( z0 ) |= |∫ |≤ 2πR = n
2π C ( z − z0 )n+1 2π R n+1 R
Liouville' s theorem : If f ( z ) is analytic and bounded for all
z then f ( z ) is a constant.
Mn!
Using Cauchy' s inequality : | f ( n ) ( z0 ) |≤
Rn
set n = 1 and let R → ∞ ⇒ | f ' ( z0 ) |= 0 ⇒ f ' ( z0 ) = 0
Since f ( z ) is analytic for all z , we may take z0 as any
point in the z - plane. f ' ( z ) = 0 for all z ⇒ f ( z ) = constant

31. 20.13 Taylor and Laurent series
Taylor’s theorem:
If f ( z ) is analytic inside and on a circle C of radius R centered
on the point z = z0 , and z is a point inside C, then
∞ ∞
f ( n ) ( z0 )
f (z) = ∑ a n ( z − z0 ) n
= ∑ n!
( z − z0 ) n
n= 0 n= 0
1 f (ξ )
2πi ∫C ξ − z
f ( z ) is analytic inside and on C, so f ( z ) = dξ where ξ lies on C
∞
1 z − z0 1 1 z − z0 n
expand
ξ −z
as a geometric series in
ξ − z0
⇒ =
ξ − z ξ − z0
∑( ξ − z0
)
n=0
1 f (ξ ) ∞ z − z0 n 1 ∞ f (ξ )
⇒ f (z) = ∑ ( ξ − z ) dξ = 2πi ∑ ( z − z0 )n ∫C (ξ − z )n+1 dξ
2πi ∫C ξ − z0 n= 0 0 n= 0 0
1 ∞ n 2πif
( n)
( z0 ) ∞ n f
(n)
( z0 )
= ∑
2πi n=0
( z − z0 )
n!
= ∑ ( z − z0 )
n!
n=0

32. If f ( z ) has a pole of order p at z = z0 but is analytic at every other point inside
and on C . Then g ( z ) = ( z − z0 ) p f ( z ) is analytic at z = z0 and expanded as a Taylor
∞
series g( z ) = ∑ bn ( z − z0 )n .
n=0
Thus , for all z inside C f ( z ) can be exp anded as a Laurent series
a− p a − p +1 a
f (z) = + + ....... + −1 + a0 + a1 ( z − z0 ) + a 2 ( z − z0 )2
( z − z0 ) p ( z − z0 ) p−1 z − z0
g ( n ) ( z0 ) 1 g( z )
a n = bn+ p and bn =
n!
=
2πi ∫ ( z − z )n+1 dz C2
0
R
1 g( z ) 1 f (z)
2πi ∫ ( z − z0 ) n+1+ p 2πi ∫ ( z − z0 ) n+1
⇒ an = dz = dz
z 0 C1
∞
f (z) = ∑ an ( z − z0 )n is analytic in a region R between
n= −∞
two circles C1 and C 2 centered on z = z0

33. ∞
f (z) = ∑ a n ( z − z0 ) n
n = −∞
(1) If f ( z ) is analytic at z = z0 , then all an = 0 for n < 0.
It may happen a n = 0 for n ≥ 0, the first non - vanishing
term is a m ( z-z0 ) m with m > 0, f ( z ) is said to have a zero
of order m at z = z0 .
(2) If f ( z ) is not analytic at z = z0
(i) possible to find a − p ≠ 0 but a − p− k = 0 for all k > 0
f ( z ) has a pole of order p at z = z0 , a −1 is called the residue of f ( z )
(ii) impossible to find a lowest value of − p ⇒ essential singularity

34. 1
Ex : Find the Laurent series of f ( z ) = 3
about the singularities
z ( z − 2)
z = 0 and z = 2. Hence verify that z = 0 is a pole of order 1 and z = 2 is a
pole of order 3, and find the residue of f ( z ) at each pole.
(1) point z = 0
−1 −1 − z ( −3)( −4) − z 2 ( −3)( −4)( −5) − z 3
f (z) = 3
= [1 + ( −3)( ) + ( ) + ( ) + ...]
8 z (1 − z / 2) 8z 2 2! 2 3! 2
1 3 3 5z 2
=− − − z− − ... z = 0 is a pole of order 1
8 z 16 16 32
(2) point z = 2 ⇒ set z − 2 = ξ ⇒ z( z − 2) 3 = ( 2 + ξ )ξ 3 = 2ξ 3 (1 + ξ / 2)
1 1 ξ ξ ξ ξ
f (z) = 3 = 3 [1 − ( ) + ( )2 − ( )3 + ( )4 − ...]
2ξ (1 + ξ / 2) 2ξ 2 2 2 2
1 1 1 1 ξ 1 1 1 1 z−2
= − + − + − .. = − + − + −
2ξ 3
4ξ 2 8ξ 16 32 2( z − 2) 3
4( z − 2) 2 8( z − 2) 16 32
z = 2 is a pole of order 3, the residue of f ( z ) at z = 2 is 1 / 8.

35. How to obtain the residue ?
a− m a−1
f (z) = + ...... + + a0 + a1 ( z − z0 ) + a 2 ( z − z0 )2 + ...
( z − z0 ) m ( z − z0 )
⇒ ( z − z0 )m f ( z ) = a − m + a − m +1 ( z − z0 ) + ....... + a −1 ( z − z0 )m −1 + ...
d m −1 ∞
⇒ m −1
[( z − z0 ) f ( z )] = ( m − 1)! a −1 + ∑ bn ( z − z0 )n
m
dz n =1
Take the limit z → z0
1 d m −1
R( z0 ) = a −1 = lim { [( z − z0 ) m f ( z )]} residue at z = z0
z → z0 ( m − 1)! dz m −1
(1) For a simple pole m = 1 ⇒ R( z0 ) = lim [( z − z0 ) f ( z )]
z → z0
g( z )
(2) If f ( z ) has a simple at z = z0 and f ( z ) = , g ( z ) is analytic and
h( z )
non - zero at z0 and h( z0 ) = 0
( z − z0 ) g ( z ) ( z − z0 ) 1 g( z )
⇒ R( z0 ) = lim = g ( z0 ) lim = g ( z0 ) lim ' = ' 0
z → z0 h( z ) z → z0 h( z ) z → z0 h ( z ) h ( z0 )

36. Ex : Suppose that f ( z ) has a pole of order m at the point z = z0 . By
considering the Laurent series of f ( z ) about z0 , deriving a general
expression for the residue R( z0 ) of f ( z ) at z = z0 . Hence evaluate
exp iz
the residue of the function f ( z ) = 2 2
at the point z = i .
( z + 1)
exp iz exp iz
f (z) = 2 2
= 2 2
poles of order 2 at z = i and z = − i
( z + 1) (z + i) (z − i)
for pole at z = i :
d d exp iz i 2
[( z − i ) 2 f ( z )] = [ 2
]= 2
exp iz − 3
exp iz
dz dz ( z + i ) (z + i) (z + i)
1 i 2 −i
R( i ) = [ e −1 − e −1 ] =
1! ( 2i ) 2 ( 2i ) 3 2e

37. 20.14 Residue theorem
f ( z ) has a pole of order m at z = z0 C
∞ γ
f (z) = ∑ a n ( z − z0 ) n
n= − m ρ • z0
I = ∫ f ( z )dz = ∫ f ( z )dz
C γ
set z = z0 + ρe iθ ⇒ dz = iρe iθ dθ
∞ ∞ 2π
I= ∑ an ∫ ( z − z0 ) dz =
C
n
∑ an ∫ 0
iρ n+1e i ( n+1)θ dθ
n= − m n= − m
2π n +1 i ( n+1)θ iρ n+1e i ( n+1)θ 2π
for n ≠ −1 ⇒ ∫ iρ e dθ = |0 = 0
0 i ( n + 1)
2π
for n = 1 ⇒ ∫ idθ = 2πi
0
I = ∫ f ( z )dz = 2πia −1
C

38. Residue theorem:
f ( z ) is continuous within and on a closed contour C
and analytic, except for a finite number of poles within C
∫C f ( z )dz = 2πi ∑ R j
j
∑ R j is the sum of the residues of f ( z ) at its poles within C
j
C C'

39. The integral I of f ( z ) along an open contour C
C
if f ( z ) has a simple pole at z = z0 ρ
⇒ f ( z ) = φ ( z ) + a−1 ( z − z0 ) −1 z0
φ ( z ) is analytic within some neighbour surrounding z0
| z − z0 |= ρ and θ1 ≤ arg( z − z0 ) ≤ θ 2
ρ is chosen small enough that no singularity of f ( z ) except z = z0
I = ∫ f ( z )dz = ∫ φ ( z )dz + a −1 ∫ ( z − z0 ) −1 dz
C C C
lim
ρ →0 C
∫ φ ( z )dz = 0
θ2 1
I = lim ∫ f ( z )dz = lim (a −1 ∫ iθ
iρe iθ dθ ) = ia −1 (θ 2 − θ1 )
ρ →0 C ρ →0 ρe θ1
for a closed contour θ 2 = θ1 + 2π ⇒ I = 2πia −1

40. 20.16 Integrals of sinusoidal functions
2π
∫0 F (cos θ , sin θ )dθ set z = exp iθ in unit circle
1 1 1 1
⇒ cos θ = ( z + ), sin θ = ( z − ), dθ = − iz −1dz
2 z 2i z
2π cos 2θ
Ex : Evaluate I = ∫ 2 2
dθ for b > a > 0
0 a + b − 2ab cos θ
1 n 1
cos nθ = ( z + z − n ) ⇒ cos 2θ = ( z 2 + z − 2 )
2 2
1 2 1
cos 2θ ( z + z − 2 )( − iz −1 )dz − ( z 4 + 1)idz
dθ = 2 = 2 2
a 2 + b 2 − 2ab cos θ 2 2 1 −1 z ( za 2 + zb 2 − abz 2 − ab )
a + b − 2ab ⋅ ( z + z )
2
i ( z 4 + 1)dz i ( z 4 + 1)
= = dz
2ab 2 2 a b 2ab 2 a b
z ( z − z ( − + ) + 1) z ( z − )( z − )
b a b a

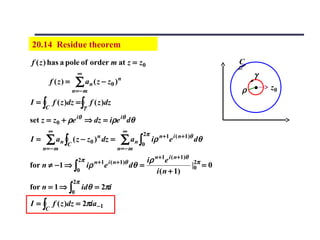
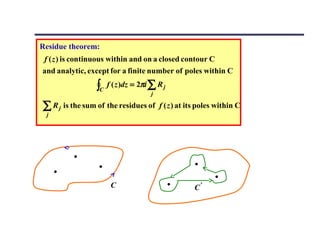
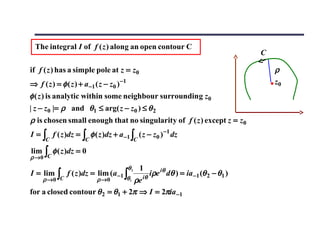
41. i z4 + 1
2ab ∫C
I= dz double poles at z = 0 and z = a / b within the unit circle
a b
z 2 ( z − )( z − )
b a
1 d m −1
Residue : R( z0 ) = lim { [( z − z0 ) m f ( z )]
z → z0 ( m − 1)! dz m −1
(1) pole at z = 0, m = 2
1 d 2 z4 + 1
R(0) = lim { [z 2 ]}
z →0 1! dz z ( z − a / b )( z − b / a )
4z 3 ( z 4 + 1)( −1)[2 z − (a / b + b / a )]
= lim { + }= a/b+b/a
z →0 ( z − a / b )( z − b / a ) 2
( z − a / b) ( z − b / a ) 2
(2) pole at z = a / b, m = 1
z4 + 1 (a / b)4 + 1 − (a 4 + b 4 )
R(a / b) = lim [( z − a / b ) 2
]= 2
=
z →a / b z ( z − a / b )( z − b / a ) (a / b) (a / b − b / a ) ab(b 2 − a 2 )
i a 2 + b2 a 4 + b4 2πa 2
I = 2πi × [ − ]= 2 2
2ab ab ab(b − a ) b (b − a 2 )
2 2

42. 20.17 Some infinite integrals
∞
∫−∞ f ( x )dx
f ( z ) has the following properties :
(1) f ( z ) is analytic in the upper half - plane, Im z ≥ 0, except for
a finite number of poles, none of which is on the real axis.
(2) on a semicircle Γ of radius R, R times the maximum of y
| f | on Γ tends to zero as R → ∞ (a sufficient condition
is that zf ( z ) → 0 as | z |→ ∞ ). Γ
0 ∞
(3) ∫ f ( x )dx and ∫0 f ( x )dx both exist
−∞ x
∞
⇒ ∫− ∞ f ( x )dx = 2π i ∑ R j −R 0 R
j
for | ∫ f ( z )dz |≤ 2π R × (maximum of | f | on Γ ), the integral along Γ
Γ
tends to zero as R → ∞ .

43. ∞ dx
Ex : Evaluate I = ∫0 2
(x + a ) 2 4
a is real
dz R dx dz
∫C ( z 2 + a 2 )4 = ∫− R ( x 2 + a 2 )4 ∫Γ ( z 2 + a 2 )4
+ as R → ∞
Γ
dz dz ∞ dx ai
⇒∫ →0⇒ ∫C ( z 2 + a 2 )4 = ∫− ∞ ( x 2 + a 2 )4
Γ ( z 2 + a 2 )4
( z 2 + a 2 )4 = 0 ⇒ poles of order 4 at z = ± ai , −R 0 R
only z = ai at the upper half - plane
1 1 1 iξ − 4
set z = ai + ξ , ξ → 0 ⇒ 2 2 4
= 2 4
= 4
(1 − )
(z + a ) ( 2aiξ + ξ ) ( 2aiξ ) 2a
1 ( −4)( −5)( −6) − i 3 − 5i
the coefficient of ξ −1 is ( ) =
( 2a ) 4 3! 2a 32a 7
∞ dx − 5i 10π 1 10π 5π
∫0 ( x 2 + a 2 )4
= 2πi (
32a 7
)=
32a 7
⇒I = ×
2 32a 7
=
32a 7

44. For poles on the real axis: y
Γ
Principal value of the integral, defined as ρ → 0
R z0 − ρ R
P∫ f ( x )dx = ∫− R f ( x )dx + ∫z + ρ f ( x )dx γ ρ
−R 0
-R 0 z0 R x
for a closed contour C
z0 − ρ R
∫C f ( z )dz = ∫− R f ( x )dx + ∫γ f ( z )dz + ∫z + ρ
0
f ( x )dx + ∫Γ f ( z )dz
R
= P∫ f ( x )dx + ∫γ f ( z )dz + ∫Γ f ( z )dz
−R
(1) for ∫ f ( z )dz has a pole at z = z0 ⇒ ∫ f ( z )dz = −πia1
γ γ
iθ
(2) for ∫ f ( z )dz set z = Re dz = i Re iθ dθ
Γ
⇒ ∫Γ f ( z )dz = ∫Γ f (Re iθ )i Re iθ dθ
If f ( z ) vanishes faster than 1 / R 2 as R → ∞, the integral is zero

45. Jordan’s lemma
(1) f ( z ) is analytic in the upper half - plane except for a finite
number of poles in Im z > 0
( 2) the maximum of | f ( z ) |→ 0 as | z |→ ∞ in the upper half - plane
(3) m > 0, then
∫Γ e
imz
IΓ = f ( z )dz → 0 as R → ∞, Γ is the semicircular contour
for 0 ≤ θ ≤ π / 2, 1 ≥ sin θ / θ ≥ π / 2 f (θ ) f = 2θ / π
| exp(imz )| = | exp(− mR sin θ )|
π
IΓ ≤ ∫Γ |e imz f ( z )||dz| ≤ MR ∫ e − mR sin θ dθ
0
f = sin θ
π/ 2 − mR sin θ
= 2 MR ∫ e dθ
0
M is the maximum of |f ( z )| on |z| = R, R → ∞ M → 0 π /2 θ
πM
π / 2 − mR ( 2θ / π ) πM
I Γ < 2 MR ∫ e (1 − e − mR ) <
dθ =
0 m m
as R → ∞ ⇒ M → 0 ⇒ I Γ → 0

46. cos mx
∞
Ex : Find the principal value of ∫− ∞ x − a dx a real, m > 0 Γ
e imz
Consider the integral I = ∫C z−a
dz = 0 no pole in the
γ ρ
−1
upper half - plane, and |( z − a ) | → 0 as |z| → ∞
-R 0 a R
e imz
I = ∫C z−a
dz
a−ρ e imx e imz R e imx e imz
= ∫− R x−a
dx + ∫γ z−a
dz + ∫a + ρ x−a
dx + ∫Γ z−a
dz = 0
e imz
As R → ∞ and ρ → 0 ⇒ ∫ dz → 0
Γ z−a
∞e imx
⇒ P∫ dx − iπa−1 = 0 and a−1 = e ima
−∞ x − a
∞ cos mx ∞ sin mx
⇒ P∫ dx = −π sin ma and P ∫ dx = π cos ma
−∞ x − a −∞ x − a

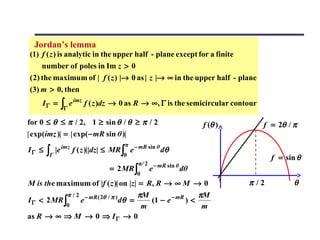
47. 20.18 Integral of multivalued functions
1/ 2
y
Multivalued functions such as z , Lnz
Single branch point is at the otigin. We let R → ∞ R Γ
and ρ → 0. The integrand is multivalued, its values
γ
along two lines AB and CD joining z = ρ to z = R A B
are not equal and opposite. ρ x
C D
∞ dx
Ex : I = ∫0 ( x + a )3 x1 / 2
for a > 0
(1) the integrand f ( z ) = ( z + a ) −3 z −1 / 2 , |zf ( z )| → 0 as ρ → 0 and R → ∞
the two circles make no contribution to the contour integral
(2) pole at z = − a , and ( − a )1 / 2 = a 1 / 2 e iπ / 2 = ia 1 / 2
1 d 3 −1 1
R( − a ) = lim [( z + a )3 ]
z → − a ( 3 − 1)! dz 3 − 1 3 1/ 2
(z + a) z
1 d 2 −1 / 2 − 3i
= lim z =
z → − a 2! dz 2 8a 5 / 2

48. − 3i
∫AB dz + ∫Γ dz + ∫DC dz + ∫γ dz = 2πi (
8a 5/2
)
and ∫ dz = 0 and ∫γ dz = 0
Γ
along line AB ⇒ z = xe i 0 , along line CD ⇒ z = xe i 2π
∞ dx 0 dx 3π
∫0, A→ B ( x + a )3 x1 / 2 ∞,C → D ( xe i 2π + a )3 x1 / 2e (1 / 2×2πi ) 4a 5 / 2
+∫ =
1 ∞ dx 3π
⇒ (1 − iπ )∫ =
e 0 ( x + a )3 x1 / 2 4a 5 / 2
∞ dx 3π
⇒∫ =
0 ( x + a )3 x1 / 2 8a 5 / 2

49. ∞ x sin x
Ex : Evaluate I (σ ) = ∫− ∞ x 2 − σ 2 dx
z sin z 1 ze iz 1 ze − iz
∫C z2 − σ 2
dz =
2i ∫C 1 z2 − σ 2
dz −
2i ∫C 2
2
z −σ 2
dz = I1 + I 2
(1) for I1 , the contour is choosed on the upper half - plane C1
due to the term e iz , and only one pole at z = σ . Γ
1 ze iz 1 −σ − ρ xe ix γ1
I1 =
2i ∫C 1 z2 − σ 2
dz =
2i ∫− R x2 − σ 2
dx
ρ
1 σ −ρ xe ix 1 ∞ xe ix -R -σ σ R
+
2i ∫−σ + ρ x2 − σ 2
dx +
2i ∫σ + ρ x 2 − σ 2 dx γ2
1 ze iz 1 ze iz 1 ze iz
+
2i ∫γ 1 z2 − σ 2
dz + ∫ 2
2i γ 2 z − σ 2
dz +
2i ∫Γ z 2 − σ 2 dz
1 σe iσ π
= 2πi × Res( z = σ ) = π = e iσ
2i 2σ 2

50. As ρ → 0 and R → ∞ ⇒ ∫ dz → 0
Γ
1 ze iz 1 − π − iσ
2i ∫γ 1 ( z + σ )( z − σ )
dz =
2i
× ( −πi )Res( z = −σ ) =
4
e
1 ze iz 1 π
∫γ dz = × πiRes( z = σ ) = e iσ
2i 2 ( z + σ )( z − σ ) 2i 4
1 ∞ xe ix π π γ1
dx + (e iσ − e − iσ ) = e iσ
2i ∫− ∞ x 2 − σ 2
I1 = σ
4 2
−σ
(2) for I 2 , we choose the lower half - plane by the
− iz Γ γ2
term e , only one pole at z = −σ
−1 ze − iz − 1 −σ − ρ xe − ix
I2 =
2i ∫C2 z 2 − σ 2 dz = 2i ∫− R x 2 − σ 2 dx C2
1 σ −ρ xe − ix 1 ∞ xe − ix 1 ze − iz
−
2i ∫−σ + ρ x2 − σ 2
dx −
2i ∫σ + ρ x2 − σ 2
dx −
2i ∫γ 1
2
z −σ 2
dz
1 ze − iz 1 ze − iz −1 ( −σ )e iσ π
− ∫γ dz − ∫Γ dz = ( ) × ( −2πi ) = e iσ
2i 2 z2 − σ 2 2i z2 − σ 2 2i − 2σ 2

51. As ρ → 0, R → ∞ ⇒ ∫ dz → 0
Γ
−1 ze − iz −1 ( −σ )e iσ π
= e iσ
2i ∫γ 1 ( z + σ )( z − σ )
dz = ( )( −πi )
2i − 2σ 4
−1 ze − iz −1 σe − iσ − π − iσ
2i ∫γ 2 ( z + σ )( z − σ )dz = (
2i
)(πi )
2σ
=
4
e
− 1 ∞ xe − ix π π
dx + (e iσ − e − iσ ) = e iσ
2i ∫− ∞ x 2 − σ 2
I2 =
4 2
− 1 ∞ xe − ix π 1
dx = e iσ − (e iσ − e − iσ )
2i ∫− ∞ x 2 − σ 2
⇒
2 4
∞ x sin x 1 ∞ xe ix 1 ∞ xe − ix
I (σ ) = ∫
2i ∫− ∞ x 2 − σ 2 2i ∫− ∞ x 2 − σ 2
dx = dx − dx
−∞ x 2 − σ 2
π π π π
= e iσ − ( e iσ − e − iσ ) + e iσ − ( e iσ − e − iσ )
2 4 2 4
π π π
= πe iσ − e iσ + e − iσ = (e iσ + e − iσ ) = π cos σ
2 2 2