This document discusses partial differential equations (PDEs). It provides examples of how PDEs can be formed by eliminating constants or functions from relations involving multiple variables. It also discusses different types of first-order PDEs and methods for solving them. Several example problems are presented with step-by-step solutions showing how to derive and solve PDEs that model different physical situations. Standard forms and techniques for reducing PDEs to simpler forms are also outlined.

1. PARTIAL DIFFERENTIAL
EQUATIONS

2. Formation of Partial Differential equations
Partial Differential Equation can be formed either
by elimination of arbitrary constants or by the
elimination of arbitrary functions from a relation
involving three or more variables .
SOLVED PROBLEMS
1.Eliminate two arbitrary constants a and b from
here R is known
( x - a)2 + ( y - b)2 + z2 = R2
constant .

3. (OR) Find the differential equation of all spheres
of fixed radius having their centers in x y- plane.
solution
( x - a)2 + ( y -b)2 + z2 = R2.......(1)
Differentiating both sides with respect to x and y
x a
=- -
2 2( )
y b
=- -
2 2( )
q
p z
¶
¶
¶
¶
= ¶
y
z z
x
z z
z
¶
x
y
=
¶
x a pz y b qz
¶
- =- - =-
,
,

4. By substituting all these values in (1)
2 2 2 2 2 2
p z + q z + z =
R
2
z R
2 2 1
2
+ +
Þ =
p q
or
1
2
z R
2 2
2
ö
+ ÷ ÷ø
æ
z
¶
+¶ ÷ø
ç çè
z
¶
=
æ
ö ¶
çè
y
x

5. 2. Find the partial Differential Equation by eliminating
arbitrary functions from
z = f (x2 - y2 )
2 2
SOLUTION
z f x y
( )..........(1)
d . wr . . to .
xandy
' 2 2
( ) 2 ......(2)
' 2 2
f x y y
( ) 2 ......(3)
z
¶
z
¶
y
f x y x
x
= - ´-
¶
= - ´
¶
= -

6. (2)
By (3)
x
=-
z
¶
ö çè
ö
÷ ÷ø
x
æ
¶
x
z
=- Þ + =0
ç çè
¶
÷ø
æ
¶
py qx
y
p
q
y
y

7. 3.Find Partial Differential Equation
by eliminating two arbitrary functions from
z = yf (x) +xg( y)
SOLUTION
z = yf (x)+xg( y)......(1)
Differentiating both sides with respect to x and y
( ) ( )........(2)
f x xg y
( ) ( )........(3)
z
¶
z
¶
y
yf x g y
x
= + ¢
¶
= ¢ +
¶

8. Again d . w .r. to x and yin equation (2)and(3)
= ¢ + ¢
f x g y
z
¶
x y
( ) ( )
¶ ¶
x (2) y (3)...... to ...
get
2
´ + ´

9. =
y z
+ ¶
¶
x z
xg y yf x xy f x g y
( ) ( ) ( ( ) ( ))
( )
ö
÷ ÷ø
æ
¶ ¶
¶
= + ¢+ ¢
z xy z
= + ¶
ç çè
z xy f g
y z
+ ¶
¶
x z
Þ ¶
¶
+ + ¢ + ¢
¶
x y
y
x
y
x
2

10. Different Integrals of Partial Differential
Equation
1. Complete Integral (solution)
Let
F x y z ¶ z
¶
z
F x y z p q
( , , , , ) = ( , , , , ) = 0......(1)
y
¶
x
¶
be the Partial Differential Equation.
The complete integral of equation (1) is given
by
f (x, y, z, a,b) = 0..........(2)

11. 2. Particular solution
A solution obtained by giving particular values to
the arbitrary constants in a complete integral is
called particular solution .
3.Singular solution
The eliminant of a , b between
=
x y z a b
f f
f
( , , , , ) 0
= ¶
=
¶
0, 0
¶
¶
a b
when it exists , is called singular solution

12. 4. General solution
In equation (2) assume an arbitrary relation
of the form . b = f (a) Then (2) becomes
f (x, y, z, a, f (a)) = 0.........(3)
Differentiating (2) with respect to a,
¶ f a
a b
¢( ) = 0..........(4)
+ ¶
¶
f f
¶
The eliminant of (3) and (4) if exists,
is called general solution

13. Standard types of first order equations
TYPE-I
The Partial Differential equation of the form
f ( p,q) = 0
has solution
z = a x + b y + c with
f (a,b) = 0
TYPE-II
The Partial Differential Equation of the form
z = px + qy + f ( p, q)
is called Clairaut’s form
of pde , it’s solution is given by
z = ax + by + f (a,b)

14. f (z, p,q) = 0
TYPE-III
If the pde is given by
then assume that
z = f
x +
ay
( )
u = x +
ay
z f
u
( )
=

15. dz
z
= ¶
¶
.1
a a dz
u
du
z
u
u
= ¶
¶
u
u
= ¶
¶
y
z
p z
q z
= ¶
¶
y
du
u
x
z
x
=
¶
¶
¶
= ¶
=
¶
¶
¶
= ¶
.
The given pde can be written as
f ( z , dz , a dz
) = 0
.And also this can
dx
dy
be integrated to get solution

16. TYPE-IV
The pde of the form f (x, p) = g( y,q)
can be
solved by assuming
f ( x , p ) = g ( y , q )
=
a
f x p = a Þ p =
f
x a
( , ) ( , )
g y q = a Þ q = Y
y a
( , ) ( , )
dz = ¶
z
dx + ¶
z
dy
¶
x
¶
y
= f
( , ) +Y( , )
dz x a dx y a dy
Integrate the above equation to get solution

17. SOLVED PROBLEMS
1.Solve the pde p2 - q = 1
and find the complete
and singular solutions
Solution
Complete solution is given by
z = ax + by + c
2
Þ = -
1
1
2
a b
- =
b a
with

18. z =ax +(a2 -1) y +c
d.w.r.to. a and c then
2
= =
1 0
z
¶
z
¶
¶
= +
¶
c
x ay
a
Which is not possible
Hence there is no singular solution
pq + p +q =0
2.Solve the pde and find the
complete, general and singular solutions

19. Solution
The complete solution is given by
z = ax +by +c
with
ab a b
+ + =
a b
1
0
= -
+
b
.......(1)
z b + +
1
x by c
= -
b
+

20. = -
1
( )
1 0
0
1
2
= =
z
¶
z
¶
¶
+ =
+
¶
c
x y
b b
no singular solution
To get general solution assume that
c = g(b)
( ).......(2)
From eq (1)
z b + +
1
x by g b
= -
b
+

21. z = -
1
+ + ¢
( ) ( ).......(3)
1
2 x y g b
¶
c b
+
¶
Eliminate from (2) and (3) to get general
solution
3.Solve the pde
z = px + qy + 1+ p2 + q2
and find the complete and singular solutions
Solution
The pde
z = px + qy + 1+ p2 + q2
is in Clairaut’s form

22. complete solution of (1) is
z =ax+by + 1+a2 +b2 .......(2)
d.w.r.to “a” and “b”
ö
........(3)
0
x a
y b
1
0
1
2 2
2 2
÷ ÷ ÷ ÷ ÷
ø
=
+ +
= +
z
¶
z
¶
¶
=
+ +
= +
¶
a b
b
a b
a

23. y b
2 2
2
From (3)
x a
x y a b
1 ( )
+ = +
1
1
2
1
1
,
1
2 2
2 2
2 2
2 2
2 2
2
2 2
2
x y
a b
a b
a b
a b
= - +
+ +
Þ
+ +
+ +
=
+ +
=

24. 2
2 2
ax a
a b
+ +
2 2
=
=
by b
a b
+ +
1 1
= Þ = - +
0 1 ( )
1
1
1
0
1
0
1
0
1
+ +
2 2 2
2 2 2
2 2
2 2
2 2
2
+
+
-
Þ + + =
=
+ +
+ + + + -
x y z
z x y
a b
z
a b
ax by a b
is required singular solution

25. 4.Solve the pde(1- x) p + (2 - y)q = 3- z
Solution
pde
- x p + - y q = -
z
= + + - -
(1 ) (2 ) 3
z px qy p q
(3 2 )
Complete solution of above pde is
z =ax +by +(3-a -2b)
5.Solve the pde p2 + q2 = z
Solution
Assume that z =f(x+ay)

26. u = x +
ay
z =f
(u)
dz
z
= ¶
¶
.1
a a dz
u
du
z
u
u
= ¶
¶
u
u
= ¶
¶
y
z
p z
q z
= ¶
¶
y
du
u
x
z
x
=
¶
¶
¶
= ¶
=
¶
¶
¶
= ¶
.
2
2
÷ø
p q z dz + a 2
æ ÷ø
dz
= 2
+ = Þ æ
2 2 z
du
du
ö çè
ö çè
From given pde

27. du
dz
z a
z
z
2
a
dz
ö çè
dz
ö du
çè
a
du
2 2
2
1
1
1
1
+
Þ =
+
= ÷ø
æ
+
= ÷ø
æ
Integrating on both sides
b
2
z x ay
a
b
a
z u
+
= +
+
+
+
=
2
1
2
1
2

28. 6. Solve the pde zpq = p + q
Solution
Assume
q = ap
Substituting in given equation
dy
zpap = p +
ap
q a
p a
= + = +
1 , 1
dx +¶
z
x
¶
dx a
z
=¶
¶
dz a
az
dy
y
dz z
z
az
Þ = 1 + + 1
+

29. zadz =(1+a)(dx+ady)
Integrating on both sides
a z 2
=(1+a)(x+ay)+b
2
7.Solve pde
pq xy
z
z
¶
¶
(or) xy
y
x
=
¶
¶
=
( )( )
Solution
q
y
p =
x

30. Assume that
y
= =
p ax q y
p
= =
,
dz pdx qdy axdx y
dy
a
a
a
q
x
= + = +
Integrating on both sides
2 2
z =a x + y +
b
a
2 2

31. 8. Solve the equation p2 + q2 = x + y
Solution
2 2
p - x = y - q =
a
p = a + x ,
q = y -
a
dz = pdx + qdy = a + xdx + y -
ady
integrating
3
3
z = a + x + y - a 2 + b
( ) 2
( )
3
2

32. Equations reducible to the standard forms
(i)If and occur in the pde as in
(xm p) ( ynq)
F(xm p, ynq) = 0 Or in F(z, xm p, ynq) = 0
Case (a) Put and
x1-m = X y1-n = Y
m ¹ 1 n ¹ 1
if ;
n
m
(1 )
n y
z
= ¶
¶
z
= ¶
¶
Y
X
z
= ¶
¶
z
Y
Y
x
p z
q z
= ¶
¶
y
m x
X
x
X
x
-
-
-
¶
¶
¶
= ¶
-
¶
¶
¶
= ¶
(1 )

33. (1 ) (1 )
n Q n
(1 ) (1 )
x m
p = ¶
z
y q = ¶
z
Y
m P m
X
n
- = -
¶
- = -
¶
z =
P z
¶ ,
= ¶
where Q
Y
X
¶
¶
Then F ( x m p , y n q ) = 0 reduces to F(P,Q) = 0
F(z, xm p, ynq) = 0 F(z, P,Q) = 0
Similarly reduces
to

34. case(b)
m = 1 n = 1
log x = X ,log y = Y
If or
put
qy Q
p = ¶
z
q =¶
z
1
Y y
px P
X x
Þ =
¶
Þ =
¶
1
(zk p) (zkq) F(zk p, zkq)
(ii)If and occur in pde as in
( , ) ( , ) 1 2 Or in f x zk p = f y zkq

35. Case(a) Put z 1 + k = Z if k ¹ -1
= + ¶
¶
k k
- - -
`1 `1
(1 ) (1 )
= + ¶
¶
- - -
z q k Q
z k Z
z k Z
Þ = +
¶
y
Z
Z
= ¶
¶
z
Z
Z
y
z
z
= ¶
¶
y
z p k P
x
x
z
x
k k
`1 `1
(1 ) (1 )
¶
¶
¶
Þ = +
¶
¶
¶
¶
Z =
Q
P Z
¶ , where
= ¶
y
x
¶
¶
Given pde reduces to
F(P,Q) and
f ( x , P ) = f ( y , Q
) 1 2

36. Case(b) if k = -1 log z = Z
-
1
z q Q
z Z
= ¶
¶
z Z
y
Z
Z
= ¶
¶
Z
Z
= ¶
¶
y
z
z
z
= ¶
¶
y
z p P
x
x
z
x
Þ =
¶
¶
¶
¶
Þ =
¶
¶
¶
¶
-
1
Solved Problems
1.Solve
p2x4 +q2 y4 = z2
2 2 2 2
ö
æ
+ ÷ ÷ø
æ
qy
px
Solution 1.......(1)
= ÷ ÷ø
ç çè
ö
ç çè
z
z

37. m n
= =
k
2, 2
=-
1
x-1 = X y-1 = Y log z = Z
= - ¶
¶
- -
2 2
= - ¶
¶
- -
zy Q
zx Z
zy Z
Y
X
X
¶
¶
Y
Y
y
z
Z
Z
p = ¶
z
q z
y
zx P
X
x
z
Z
Z
x
2 2
= -
¶
¶
¶
¶
¶
= ¶
= ¶
¶
= -
¶
¶
¶
= ¶
¶
Z =
Q
P Z
¶ , where
= ¶
Y
X
¶
¶

38. Q
px = - = -
P qy
z
z
2 2
,
( ) ( )
2 2
+ =
P Q
- + - =
P Q
1
1
2 2
(1)becomes
Z aX bY c
= + +
a 2 + b 2 = 1, b = 1
-
a
2
log 1
2 2 2
z = ax + - a y +
c

39. 2. Solve the pde p2 + q2 = z2 (x2 + y2 )
SOLUTION
p = + ÷ø
( 2 2 ).....(1)
2 2
x y
q
z
z
æ + ÷ø
ö çè
çè
æ
ö k =-1 log z = Z
-
1
z q Q
z Z
= ¶
¶
z Z
y
Z
Z
= ¶
¶
y
z
z
= ¶
¶
= ¶
¶
Z
z
z
y
z p P
x
x
Z
x
Þ =
¶
¶
¶
¶
Þ =
¶
¶
¶
¶
-
1

40. Eq(1) becomes
P 2 + Q 2 = ( x 2 +
y
2 ).....(2)
P 2 - x 2 = y 2 - Q 2 =
a
2
x a x
1 2 2
b
2
z a x
ö çè
y y a a y
ö a
çè
a
+ ÷ø
- æ
-
+ + + ÷ø
= æ
-
-
1
2 2 2
cosh
( )
2 2
( )
2
sinh
2
log

41. Lagrange’s Linear Equation
Def: The linear partial differenfial equation
of first order is called as Lagrange’s linear Equation.
This eq is of the form Pp + Qq = R
Where P , Q and R are functions x,y and z
The general solution of the partial differential
equation P p + Q q = R is F(u,v) = 0
Where is arbitrary function of
and
F 1 u(x, y, z) = c
2 v(x, y, z) = c

42. Here u = c and v = 1 c2 are independent solutions
dz
of the auxilary equations
R
dx = dy
=
Q
P
Solved problems
1.Find the general solution of x2 p + y2q = (x + y)z
Solution
dx
dy
dz
auxilary equations are = =
x
2 y
2 ( x + y )
z

43. dy
dx
=
Integrating on both sides
2 y
2
u x y c
( - 1 -
1
) 1
x
= - =
2 2 ( )
x y z
( )
( )( ) ( )
dz
z
dx -
dy
d x -
y
d x -
y
( )
x y
dz
x y z
x y x y
dz
x y
=
-
+
=
- +
+
=
-
( )
Integrating on both sides

44. x - y = z +
c
= - =
log( ) log log
v x y z c
2
1
2
( )
-
The general solution is given by F(u,v) = 0
F(x-1 - y-1,(x - y)z-1) = 0
2.solve x2 (y - z) + y2 (z - x)q = z2 (x - y)
solution Auxiliary equations are given by
dz
dy
dx
2 ( ) y 2 ( z x
) z2 (x y)
x y z
-
=
-
=
-

45. dz
dy
dx
2 2 2
z
y
x
( ) ( ) ( )
dy
+ +
dz
dx
2 2 2
y - z + z - x + x -
y
( ) ( ) ( )
0
dz
dy
+ + =
dx
2 2 2
-
=
-
=
-
z
y
x
z
y
x
x y
z x
y z
Integrating on both sides

46. u =1 +1 +1 =
a
x y z
- - -
1 1 1
z dz
z x y
y dy
y z x
x dx
x y z
( ) ( ) ( )
1 1 1
+ +
x y - z + y z - x + z x -
y
( ) ( ) ( )
0
dz
dy
+ + =
-
=
-
=
-
- - -
z
y
dx
x
x dx y dy z dz
Integrating on both sides
v = xyz =b

47. The general solution is given by
F(x-1 + y-1 + z-1, xyz) = 0
HOMOGENEOUS LINEAR PDE WITH
CONSTANT COEFFICIENTS
Equations in which partial derivatives
occurring are all of same order (with degree
one ) and the coefficients are constants ,such
equations are called homogeneous linear PDE
with constant coefficient

48. a z
n
a z
a z
+ ¶
+ ¶
+ ¶
........ ( , ) 1 1 2 2 2 F x y
¢ = ¶
= ¶
¶
Assume that , .
y
D
x
D
¶
¶
nth
then order linear homogeneous equation is
given by
n + n- ¢ + n- ¢ + + ¢ =
1 D a D D a D D a D n z F x y
n
( 2 2 ......... ) ( , )
2
1
or
f (D,D¢)z = F(x, y).........(1)
y
x y
x y
x
z
n
n
n n
n
n
n
n
=
¶
¶ ¶
¶ ¶
¶
- -

49. The complete solution of equation (1) consists
of two parts ,the complementary function and
particular integral.
The complementary function is complete
solution of equation of f (D,D¢)z = 0
Rules to find complementary function
Consider the equation
k z
0 2
2
+ ¶
2
2
k z
+ ¶
2 1
2
=
¶
¶ ¶
¶
¶
y
x y
x
z
or
D2 + k DD¢ + k D¢ z =
( 2 ) 0.............(2)
1 2

50. The auxiliary equation for (A.E) is given by
D2 + k DD¢ + k D¢ =
D = m,D¢ =1
And by giving
2 0
1 2
m2 + k m+ k =
The A.E becomes 0....(3) 1 2
Case 1
If the equation(3) has two distinct roots 1 2 m ,m
The complete solution of (2) is given by
( ) ( ) 1 1 2 2z = f y + m x + f y + m x

51. Case 2
If the equation(3) has two equal roots i.e 1 2 m = m
The complete solution of (2) is given by
( ) ( ) 1 1 2 1z = f y +m x +xf y +m x
Rules to find the particular Integral
Consider the equation
D2 + k DD¢+ k D¢ z = F x y
( 2 ) ( , )
1 2
f (D,D¢)z = F(x, y)

52. Particular Integral (P.I)
F x y
( , )
f D D
¢
( , )
=
Case 1 If
F(x, y) = eax+by
then P.I=
¢
ax +
by
= ¹
, ( , ) 0
1
( , )
1
( , )
+
e f a b
f a b
e
f D D
ax by
D - a ¢
f (a,b) = 0 ( D )
If and is
b
factor of f (D,D¢)
then

53. P.I =xeax+by
If and D - a ¢
is
factor of
2
then P.I
F(x, y) = sin(mx +ny)or cos(mx +ny)
= +
sin( )
mx ny
= +
2 2 f m2 mn n2
( , , )
sin( )
( , , )
mx ny
f D DD D
- - -
¢ ¢
Case 2
P.I
f (a,b) = 0 ( D )2
b
f (D,D¢)
= x eax+by
2

54. Case 3
F(x, y) = xm yn
1 = ¢ -
xm yn [ f D D ] xm yn
f D D
( , ) 1
¢
( , )
P.I =
[ ( , )] 1 Expand f D D ¢ - in ascending powers of
D or D ¢ and operating on x m y n term by term.
Case 4 when is any function of x
and y.
P.I=
F(x, y)
1 F x y
( , )
f D D¢
( , )
1 ( , ) ( , )
=ò -
- ¢
F x y F x c mx dx
D mD

55. (D -mD¢) f (D,D¢)
Here is factor of
(y + mx)
Where ‘c’ is replaced by after integration
Solved problems
1.Find the solution of pde
(D3 - D¢3 + 3DD¢2 - 3D2D¢)z = 0
Solution
The Auxiliary equation is given by

56. Solution
The Auxiliary equation is given by
m3 -1+3m-3m2 = 0
By taking
D = m,D¢ = 1
m =1,1,1.
2
1 2 = f y + x + xf y + x + x f y + x
Complete solution ( ) ( ) ( ) 3
2. Solve the pde (D3 + 4D2D¢ - 5DD¢)z = 0
Solution
The Auxiliary equation is given by

57. 3 2
m m m
+ - =
4 5 0
= -
0,1, 5
z f y f y x f y x
( ) ( ) ( 5 )
1 2 3
m
= + + + -
3. Solve the pde (D2 + D¢2 )z = 0
Solution
the A.E is given by m2 +1=0
m = ±i
( ) ( ) 1 2 z = f y + ix + f y - ix

58. 4. Find the solution of pde
(D2 + 3DD¢ - 4D¢2 )z = e2x+ 4 y
Solution
Complete solution =
Complementary Function + Particular Integral
m2 + 3m- 4 = 0
The A.E is given by
m =-4,1
. ( ) ( 4 ) 1 2 C F = f y + x +f y - x

59. 2 4
P I e
3 4 36
.
2 4
2 2
-
=
+ ¢- ¢
=
x+ y e x+ y
D DD D
Complete solution
= C.F + P.I
e x y y x y x
36
( ) ( 4 )
2 4
1 2
+
= f + +f - -

60. 5.Solve (D3 - 3DD¢ + 2D¢3 )z = e2x- y + ex+ y
Solution
3
A E m m
= - +
. 3 2
= -
1,1, 2.
C F y x x y x y x
. ( ) ( ) ( 2 )
1 2 3
m
= f + + f + + f
-
x y 2
x y
2
e
P I e
=
. 2 2
1 D 3 - DD ¢ 2 + D
¢
3
D D D D
- ¢ + ¢
3 2 ( ) ( 2 )
=
- -

61. 2
P I e
- -
( ) ( 2 ) 9
.
2
2
1
x y xe x y
D D D D
=
- ¢ + ¢
=
x y x y
P I e
2 3 2 3 2 2
x y
P I x e
e
D D D D
D DD D
+
+ +
=
- ¢ + ¢
=
- ¢ + ¢
=
6
.
3 2 ( ) ( 2 )
.
2
2
1 2 z = C.F + P.I + P.I

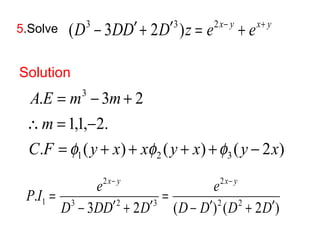
62. x y
x -
y
z = y + x + x y + x + y - x + xe +
x e +
9 6
( ) ( ) ( 2 )
2 2
1 2 3 f f f
6.Solve (D2 -DD¢)z =cos x cos 2y
Solution
(D2 -DD¢)z = 1 x + y + x - y
[cos( 2 ) cos( 2 )]
2
2
A E m m
. 0
0,1
C F y x y
. ( ) ( )
1 2
m
=f + +f
=
= - =

63. P I x y = +
. cos( 2 ) 1 2 x y x y
cos( 2 )
= +
cos( 2 )
(( 1) ( 2))
= +
D DD
( )
- - -
- ¢
P I x y
= - = x -
y x y
D DD
. cos( 2 ) 2 2 -
cos( 2 )
3
cos( 2 )
(( 1) (2))
( )
= -
- -
- ¢
( ) ( ) cos( 2 ) 1 1 2 z = f y + x +f y - x + x + y - x - y
cos( 2 )
3
7.Solve (D2 + DD¢ - 6D¢2 )z = x2 y2
Solution
. 2 6 0
= -
A E m m
= + - =
2, 3.
m

64. . ( 2 ) ( 3 ) 1 2 C F = f y + x +f y - x
2 2
2
2
æ ¢
2
2
2
æ ¢
æ ¢
2
P I x y
D
é
1 1 6
é
D 2
D
2 2
1
2
2
2 2
2 2
6
D
D
D
ù
ö
ö
1 6 6
.
x y
D
D
D
D
D
x y
D
D
D
D DD D
ù
ú ú
û
ê ê
ë
ö
÷ ÷ø
ç çè
-
¢
+ ÷ ÷ø
ç çè
-
¢
= -
úû
êë
÷ ÷ø
ç çè
-
¢
= +
+ ¢ - ¢
=
-
-

65. é ¢
ö
D D
1 6
2
D
D
2 2
2
x
D x y x y
2 6 2 2
2
x
3 4 4
D x y x y 6 2
x x
3 4
D x y x y 8 2
x
ù
úû
é
é
2 2 2
é
æ ¢
æ
-
-
-
2 2 2
= + +
é
= + +
êë
ù
ö
ö
ù
úû
êë
ù
ù
úû
êë
2
+ ÷ ÷ø
ç çè æ
= - -
úû
êë
+ ÷ ÷ø
ç çè
= - -
úû
êë
+ ÷ ÷ø
ç çè
-
¢
= -
-
2
90
2
60
12
12
3
2
12
12
3
2
4 2 5 6
2
2
2 2 2
2 2
2
2
2
x y x y x
D
D
D
x y
D
D
D

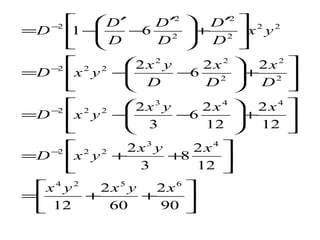
66. 7.Solve (D2 - 5DD¢ + 6D¢2 )z = y sin x
Solution
A.E is m2 - 5m+ 6 = 0
m =3,m = 2.
C . F =P . I f ( y y sin x
+ 3 x ) +f ( y + 2 x
) 1 2 2
2 y x
y x
sin
sin
ù
é
[ ]
[ x x x y x x]
1
1
1
1
D D
a x x x x
D D
a x xdx
D D
D D
D D
D D D D
D DD D
2 cos 2sin ( 2 ) cos
( 3 )
cos 2( cos sin )
( 3 )
( 2 )sin
( 3 )
( 2 )
( 3 )
( 3 )( 2 )
5 6
- - +
- ¢
=
- - - +
- ¢
=
-
- ¢
=
úû
êë
- ¢ - ¢
=
- ¢ - ¢
=
- ¢ + ¢
=
ò

67. P I y x
. sin 2 2
y x
y x
sin
sin
ù
é
here
= +2
[ ]
[ x x x y x x]
1
1
1
1
D D
a x x x x
D D
a x xdx
D D
D D
D D
D D D D
D DD D
2 cos 2sin ( 2 ) cos
( 3 )
cos 2( cos sin )
( 3 )
( 2 ) sin
( 3 )
( 2 )
( 3 )
( 3 )( 2 )
5 6
- - +
- ¢
=
- - - +
- ¢
=
-
- ¢
=
úû
êë
- ¢ - ¢
=
- ¢ - ¢
=
- ¢+ ¢
=
ò (a y x)

68. [ y x x
]
1
=
D D
= ò ( - ( b - 3 x )cos x -
2sin x )
dx
(b y x)
b x x x x x
= - + + +
sin 2cos 3( sin cos )
y x x x x x x
= - + + + +
( 3 )sin 2cos 3( sin cos )
x y x
5cos sin
cos 2sin
( 3 )
= -
- -
- ¢
here
= +3

69. Non Homogeneous Linear PDES
If in the equation f (D,D¢)z = F(x, y)............(1)
the polynomial expression f (D,D¢)
is not
homogeneous, then (1) is a non- homogeneous
linear partial differential equation
Ex (D2 + 3D + D¢ - 4D¢2 )z = e2x+3 y
Complete Solution
= Complementary Function + Particular Integral
To find C.F., factorize
into factors of the form
f (D,D¢)
(D -mD¢-c)

70. If the non homogeneous equation is of the form
- ¢ - - ¢ - =
D m D c D m D c z F x y
( )( ) ( , )
1 1 2 2
= c x + + c x +
C F e 1 f y m x e 2 f
y m x
. ( ) ( )
1 2
1.Solve (D2 -DD¢+D)z = x2
Solution
f (D,D¢) = D2 - DD¢ + D = D(D - D¢ +1)
. ( ) ( ) 1 2 C F =e-xf y +x +f y

71. 2
D
P I x
. 1 1 ( 1)
x D
x D
1 ( 1) ( 1) ......
ù
úû
é ¢ +
= -
é ¢ +
+ úûù
é
ù
+ + = úû
êë
ù
é
é
é ¢ +
= + +
êë
ù
ú úû
ê êë
ù
+ úû
êë
êë
= +
úû
êë
- ¢ +
=
-
3 12 3.4 3.4.5 12.5.6
1
3 4 4 5 6
2
2
2
2
2 2
2
2
1
2 2
x x x x x x
D
x
D
D
D
x
D
D DD D D

72. 2.Solve (D +D¢-1)(D + 2D¢-3)z = 4
Solution
( ) ( 2 ) 4 1
3
z =exf y -x +e 3
xf y - x +
1