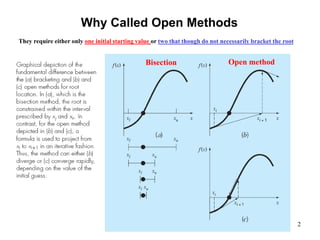
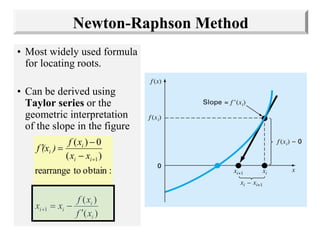
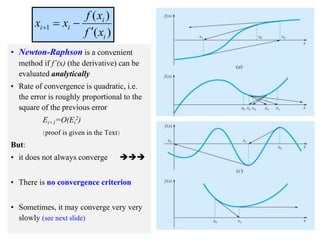
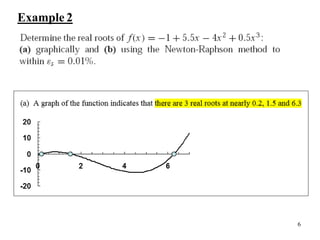
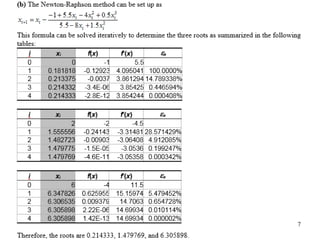
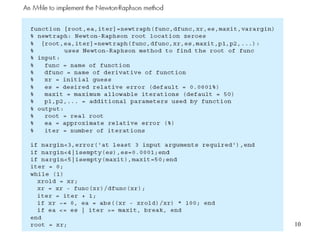
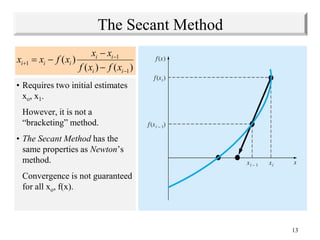
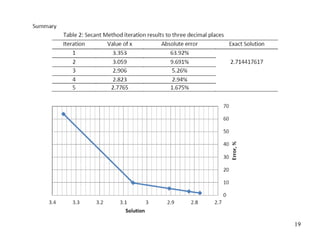
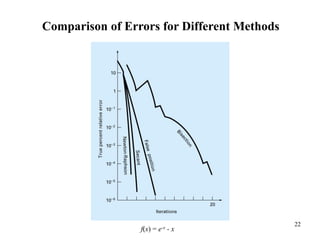
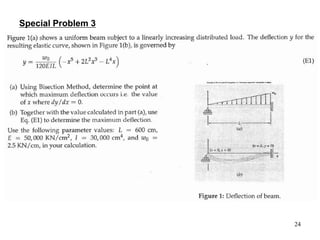
The document discusses various numerical methods for finding the roots of functions, including the Newton-Raphson method, secant method, and bisection method. The Newton-Raphson method uses the tangent line approximation at each iteration to quickly converge on roots. It has quadratic convergence but may not always converge. The secant method is similar but computes the derivative numerically when an analytical derivative is not available. Bisection is a bracketing method that uses two initial values to successively narrow the range containing the root. Multiple roots can pose problems as the function value reaches zero before the derivative at the root, preventing convergence of Newton-Raphson and secant methods which rely on the derivative. Special functions

1. 1
Chapter 6
Open Methods

2. 2
Why Called Open Methods
They require either only one initial starting value or two that though do not necessarily bracket the root
Bisection Open method

3. Newton-Raphson Method
• Most widely used formula
for locating roots.
• Can be derived using
Taylor series or the
geometric interpretation
of the slope in the figure
)
(
)
(
:
obtain
to
rearrange
)
(
0
)
(
1
1
i
i
i
i
i
i
i
i
x
f
x
f
x
x
x
x
x
f
)
(x
f










4. 4
• Newton-Raphson is a convenient
method if f’(x) (the derivative) can be
evaluated analytically
• Rate of convergence is quadratic, i.e.
the error is roughly proportional to the
square of the previous error
Ei+1=O(Ei
2)
(proof is given in the Text)
But:
• it does not always converge 
• There is no convergence criterion
• Sometimes, it may converge very very
slowly (see next slide)
)
(
)
(
1
i
i
i
i
x
f
x
f
x
x





5. 5
Example 1: Slow Convergence
1
:
of
roots
positive
the
Find
10

 x
f(x)
Iteration x
0 0.5
1 51.65
2 46.485
3 41.8365
4 37.65285
5 33.887565
.
.
38 1.083
∞ 1.0000000
5
.
0
use
10
1
9
10
1 



 o
i
i
i
i x
x
x
x
x
:
Formula
R
-
N

6. 6
Example 2

7. 7

8. 8
Example 3

9. 9

10. 10

11. 11
Newton-Raphson Method: Drawbacks
 The Newton-Raphson method requires the calculation of the
derivative of a function, which is not always easy.
 If f' vanishes at an iteration point, then the method will fail to
converge.
 When the step is too large or the value is oscillating, other
more conservative methods should take over the case.

12. The Secant Method
• If derivative f’(x) can not be computed analytically then we need to
compute it numerically (backward finite divided difference method)
RESULT: N-R becomes SECANT METHOD
1
1
1










i
i
i
i
i
i
i
i
i
x
x
x
f
x
f
dx
df
x
f
x
f
x
f
x
x
)
(
)
(
)
(
)
(
'
)
(
:
Raphson
-
Newton

,
,
,
)
(
)
(
)
(
:
Secant 3
2
1
1
1
1 






 i
x
f
x
f
x
x
x
f
x
x
i
i
i
i
i
i
i

13. 13
• Requires two initial estimates
xo, x1.
However, it is not a
“bracketing” method.
• The Secant Method has the
same properties as Newton’s
method.
Convergence is not guaranteed
for all xo, f(x).
)
(
)
(
)
(
1
1
1







i
i
i
i
i
i
i
x
f
x
f
x
x
x
f
x
x
The Secant Method

14. 14
)
(
'
)
(
:
Raphson
-
Newton
i
i
i
i
x
f
x
f
x
x 

1
Modified Secant Method
)
(
)
(
)
(
:
Secant
Original
1
1
1







i
i
i
i
i
i
i
x
f
x
f
x
x
x
f
x
x
)
(
)
(
)
(
:
formula
R
-
N
original
the
in
)
(
)
(
)
(
'
compute
to
fraction
on
perturbati
small
a
Use
:
Secant
Modified
i
i
i
i
i
i
i
i
i
i
i
i
x
f
x
x
f
x
x
f
x
x
x
x
f
x
x
f
x
f













1

15. 15

16. 16
)
(
)
(
)
(
1
1
1
:
Secant
Original







i
i
i
i
i
i
i
x
f
x
f
x
x
x
f
x
x
Example 4

17. 17
Example 5

18. 18

19. 19

20. 20
Example 6

21. 21
Complete

22. 22
Comparison of Errors for Different Methods
f(x) = e-x - x

23. 23
Multiple Roots
f(x) = (x-3)(x-1)2
f(x) = (x-3)(x-1)3
f(x) = (x-3)(x-1)4
1. The function does not change sign at even
multiple roots – the bracket methods can not be
used, only open methods can be used.
2. f’(x) also goes to 0 at the roots. This causes
problem for both Newton-Raphson and Secant
methods since they require derivative f’(x) in the
denominator, causing divided by 0.
(one help: f(x) always reaches 0 before f’(x))

24. 24
Special Problem 3

25. 25
Use the bisection, Newton-Raphson and Second Methods to find
the root for the following problems
Home Work

26. 26
5.