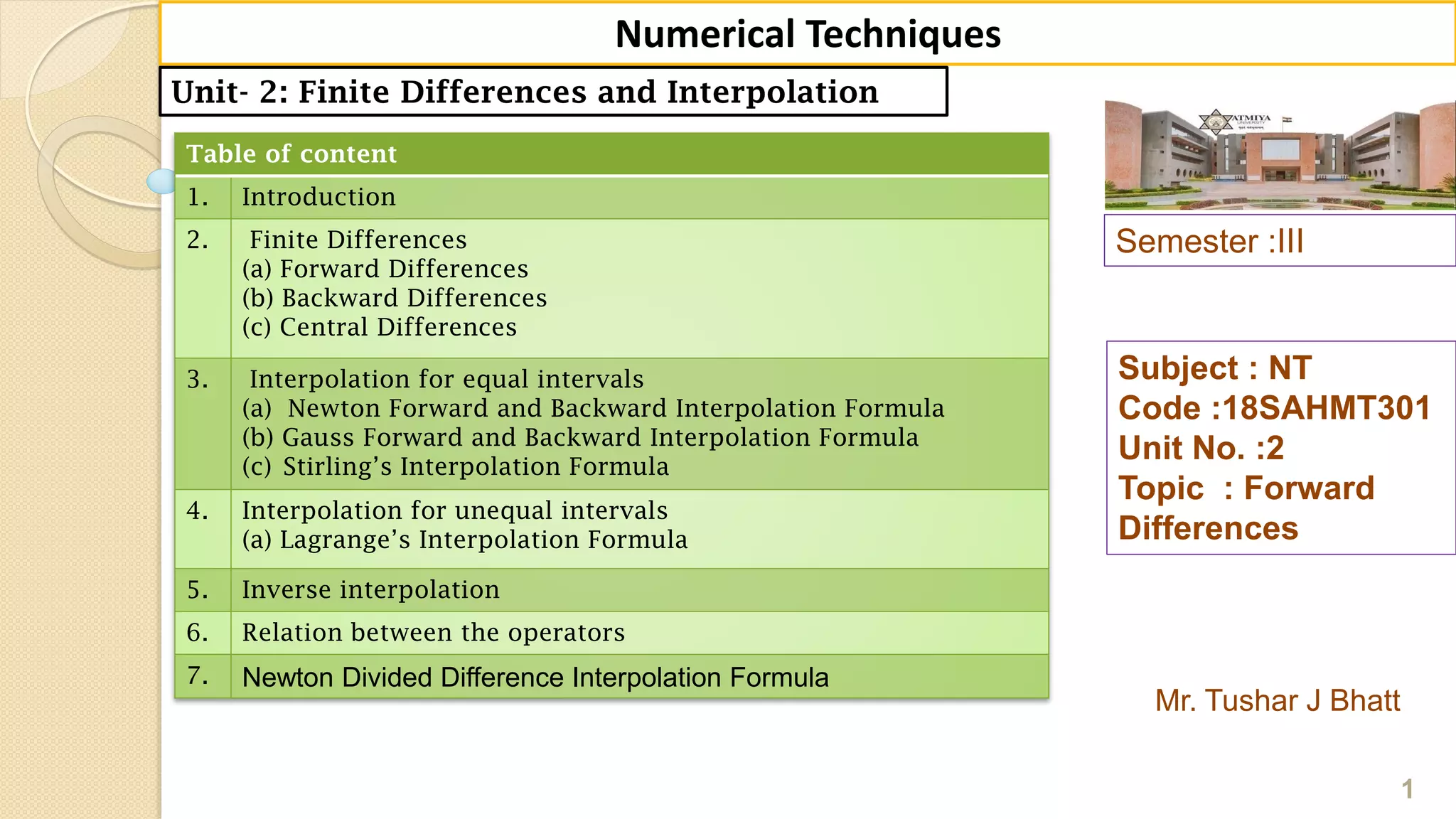
The document outlines the topic of 'Forward Differences' as part of a course on numerical techniques, emphasizing finite differences and interpolation methods. It includes definitions, types of differences (forward, backward, and central), and presents various interpolation formulas like Newton's and Lagrange's. Additionally, it details the properties of the operators and provides examples and tables for better understanding.

1. Semester :III
Mr. Tushar J Bhatt
Subject : NT
Code :18SAHMT301
Unit No. :2
Topic : Forward
Differences
1
Numerical Techniques
Unit- 2: Finite Differences and Interpolation
Table of content
1. Introduction
2. Finite Differences
(a) Forward Differences
(b) Backward Differences
(c) Central Differences
3. Interpolation for equal intervals
(a) Newton Forward and Backward Interpolation Formula
(b) Gauss Forward and Backward Interpolation Formula
(c) Stirling’s Interpolation Formula
4. Interpolation for unequal intervals
(a) Lagrange’s Interpolation Formula
5. Inverse interpolation
6. Relation between the operators
7. Newton Divided Difference Interpolation Formula

2. Semester :III
Mr. Tushar J Bhatt
Subject : NT
Code :18SAHMT301
Unit No. :2
Topic : Forward
Differences
2
Numerical Techniques
Unit- 2: Finite Differences and Interpolation
D efinition : Finite D ifferences
0 1 1 1
L et ( , ) ; 0,1, 2, ..., b e an y set o f d ata va lu es fo r th e fu n ctio n
( ) w ith th e valu es are eq u ally sp aced , d istan ce ap art so
th at ... ; th at is , an d ( ).
S o th e val
i i
i
n n i i i i
x y i n
y f x x h
x x x x x x h y f x 


      
1
0 1
0 1
u e o f is k n o w n as th e F in ite d ifferen c e
b etw een tw o co n secu tive term s o f .
S u p p o se th at , , ..., b e th e set o f valu es o f co rresp o n d in g
to th e valu es o f as , , ..., th en th e ex p re
i i
n
n
h x x
x
y y y y
x x x x

 
1 0 2 1 1
ssio n lik e
y , y , ..., y are called th e d ifferen ces o f .n n
y y y y
  

3. Semester :III
Mr. Tushar J Bhatt
Subject : NT
Code :18SAHMT301
Unit No. :2
Topic : Forward
Differences
3
Numerical Techniques
There are three types of finite differences as follows :
Finite
Differences
Forward
Difference
Backward
Difference
Central
Difference

4. Semester :III
Mr. Tushar J Bhatt
Subject : NT
Code :18SAHMT301
Unit No. :2
Topic : Forward
Differences
4
Numerical Techniques
Unit- 2: Finite Differences and Interpolation
Definition : Forward Difference
0 1 0
1 2 1
2 3 2
1
T h e d iffe re n c e b e tw e e n tw o c o n se c u tiv e v a lu e s o f y is c a lle d
th e fo rw a rd d iffe re n c e a n d it is d e n o te d b y .
M a th e m a tic a lly w e e x p re ss it a s fo llo w s:
,
,
,
.
.
.
w h e rei i i
y y y
y y y
y y y
y y y i

  
  
  
    0 ,1, 2 ..., .n
1st forward
difference

5. Semester :III
Mr. Tushar J Bhatt
Subject : NT
Code :18SAHMT301
Unit No. :2
Topic : Forward
Differences
5
Numerical Techniques
Unit- 2: Finite Differences and Interpolation
Definition : Forward Difference
2
2
0 0 1 0 1 0
2
1 1 2 1 2 1
2
2 2 3 2 3 2
2
1
T h e S e c o n d fo rw a rd d iffe re n c e is d e n o te d b y .
M a th e m a tic a lly w e e x p re ss it a s fo llo w s:
( ) ( ) ,
( ) ( ) ,
( ) ( ) ,
.
.
.
( ) ( )i i i i
y y y y y y
y y y y y y
y y y y y y
y y y y

          
          
          
        1
w h e re 0 ,1, 2 ..., .
i i
y y
i n

  

2nd forward
difference

6. Semester :III
Mr. Tushar J Bhatt
Subject : NT
Code :18SAHMT301
Unit No. :2
Topic : Forward
Differences
6
Numerical Techniques
Unit- 2: Finite Differences and Interpolation
Definition : Forward Difference
1 1 1 1
1 1
S im ilarly w e o b tain ed th e n fo rw ard d ifferen ce is d en o ted b y .
M ath em atically w e ex p ress it as fo llo w s:
( ) ( )
w h ere 0 ,1, 2 ..., .
th n
n n n n n
i i i i i i
y y y y y y
i n
   
 

          

nth forward
difference

7. Semester :III
Mr. Tushar J Bhatt
Subject : NT
Code :18SAHMT301
Unit No. :2
Topic : Forward
Differences
7
Numerical Techniques
A bove all the form ulae w e show n in the follow ing tabular form :
x y 
2

3

4

0
x 0
y
1
x 1
y
2
x 2
y
3
x 3
y
4
x 4
y
0
y
1
y
2
y
3
y
2
0
y
2
1
y
2
2
y
3
0
y
3
1
y
4
0
y

8. Semester :III
Mr. Tushar J Bhatt
Subject : NT
Code :18SAHMT301
Unit No. :2
Topic : Forward
Differences
8
Numerical Techniques
P roperties of the operator :
   1 . [ ( ) ( )] ( ) ( )
w h ere ' ' an d ' ' are co n stan ts.
a f x b g x a f x b g x
a b
     
 2 . [ ( ) ] ( ) w h ere 'c' is co n stan t.c f x c f x  
 3 . ( ) ( )
w h e re ' ' a n d ' ' a re p o s itiv e in te g e rs .
m n m n
f x f x
m n

   
 4 . [ ( ) ( )] ( ) ( )f x g x f x g x    
5 . [ ] 0 w h ere 'c' is co n stan tc 

9. Semester :III
Mr. Tushar J Bhatt
Subject : NT
Code :18SAHMT301
Unit No. :2
Topic : Forward
Differences
9
Numerical Techniques
2
2 3
E x -1 : C o n stru ct th e fo rw ard tab le fo r ( ) ; 0,1, 2, 3, 4 an d fin d
th e valu es o f ( (2 )), (1), (0 ).
f x x x
f
 
  
x y 
2

3

4

0
0x  0
0y 
1
1x  1
1y 
2
2x  2
4y 
3
3x  3
9y 
4
4x  4
1 6y 
0
1y 
1
3y 
2
5y 
2
0
2y 
2
1
2y 
3
0
0y 
3
7y 
2
1
2y 
3
1
0y 
4
0
0y 

10. Semester :III
Mr. Tushar J Bhatt
Subject : NT
Code :18SAHMT301
Unit No. :2
Topic : Forward
Differences
10
Numerical Techniques
2
T o fin d : (a ) ( ( 2 ))
N o w ( 2 ) = 4
( ( 2 )) ( 4 ) ( ) 5 .
f
f
f y

     
2
2 2
1
T o fin d : (b ) (1)
(1) ( ) 2 .y

    
3
3 3
0
T o fin d : (c ) ( 0 )
( 0 ) ( ) 0 .y

    

11. Semester :III
Mr. Tushar J Bhatt
Subject : NT
Code :18SAHMT301
Unit No. :2
Topic : Backward
Differences
11
Numerical Techniques
Definition : Backward Difference
1 1 0
2 2 1
3 3 2
1
T h e d iffe re n c e b e tw e e n tw o c o n se c u tiv e v a lu e s o f y is c a lle d
th e b a c k w a rd d iffe re n c e a n d it is d e n o te d b y .
M a th e m a tic a lly w e e x p re ss it a s fo llo w s:
,
,
,
.
.
.
w h e rei i i
y y y
y y y
y y y
y y y i

  
  
  
   1, 2 ..., .n
1st backward
difference

12. Semester :III
Mr. Tushar J Bhatt
Subject : NT
Code :18SAHMT301
Unit No. :2
Topic : Backward
Differences
12
Numerical Techniques
Definition : Backward Difference
2nd forward
difference
2
2
1 1 1 0 1 0
2
2 2 2 1 2 1
2
3 3 3 2 3 2
2
1
T h e S e c o n d fo rw a rd d iffe re n c e is d e n o te d b y .
M a th e m a tic a lly w e e x p re s s it a s fo llo w s :
( ) ( ) ,
( ) ( ) ,
( ) ( ) ,
.
.
.
( ) ( )i i i i
y y y y y y
y y y y y y
y y y y y y
y y y y 

          
          
          
        1
w h e re 1, 2 ..., .
i i
y y
i n

  


13. Semester :III
Mr. Tushar J Bhatt
Subject : NT
Code :18SAHMT301
Unit No. :2
Topic : Backward
Differences
13
Numerical Techniques
1 1 1 1
1 1
S im ilarly w e o b tain ed th e n b ack w ard d ifferen ce is d en o ted b y .
M ath em atically w e ex p ress it as fo llo w s:
( ) ( )
w h ere 1, 2 ..., .
th n
n n n n n
i i i i i i
y y y y y y
i n
   
 

          

nth
backward
difference
Definition : Backward Difference

14. Semester :III
Mr. Tushar J Bhatt
Subject : NT
Code :18SAHMT301
Unit No. :2
Topic : Backward
Differences
14
Numerical Techniques
A bove all the form ulae w e show n in the follow ing tabular form :
x y 
2

3

4

0
x 0
y
1
x 1
y
2
x 2
y
3
x 3
y
4
x 4
y
1
y
2
y
3
y
4
y
2
2
y
2
3
y
2
4
y
3
3
y
3
4
y
4
4
y

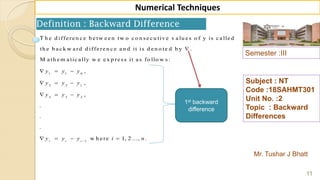
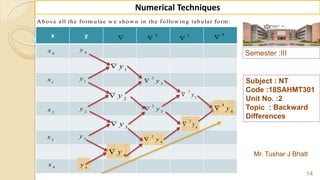
15. Semester :III
Mr. Tushar J Bhatt
Subject : NT
Code :18SAHMT301
Unit No. :2
Topic : Backward
Differences
15
Numerical Techniques
P roperties of the operator :
   1 . [ ( ) ( )] ( ) ( )
w h ere ' ' an d ' ' are co n stan ts.
a f x b g x a f x b g x
a b
     
 2 . [ ( ) ] ( ) w h ere 'c' is co n stan t.c f x c f x  
 3 . ( ) ( )
w h e re ' ' a n d ' ' a re p o s itiv e in te g e rs .
m n m n
f x f x
m n

   
 4 . [ ( ) ( )] ( ) ( )f x g x f x g x    
5 . [ ] 0 w h ere 'c' is co n stan tc 

16. Semester :III
Mr. Tushar J Bhatt
Subject : NT
Code :18SAHMT301
Unit No. :2
Topic : Central
Difference
16
Numerical Techniques
Definition : Central Difference
1 1 0
2
3 2 1
2
5 3 2
2
2 1 1
2
T h e d iffe re n c e b e tw e e n tw o c o n se c u tiv e v a lu e s o f y is c a lle d
th e b a c k w a rd d iffe re n c e a n d it is d e n o te d b y .
M a th e m a tic a lly w e e x p re ss it a s fo llo w s:
,
,
,
.
.
.
i i i
y y y
y y y
y y y
y y y




  
 
 
 
  w h e re 1, 2 ..., .i n
1st central
difference

17. Semester :III
Mr. Tushar J Bhatt
Subject : NT
Code :18SAHMT301
Unit No. :2
Topic : Central
Difference
17
Numerical Techniques
A bove all the form ulae w e show n in the follow ing tabular form :
x y 
2

3

0
x 0
y
1
x 1
y
2
x 2
y
3
x 3
y
1
2
y
3
2
y
5
2
y
2
1
y
2
2
y
3
3
2
y

18. Semester :III
Mr. Tushar J Bhatt
Subject : NT
Code :18SAHMT301
Unit No. :2
Topic :
Interpolation
18
Numerical Techniques
Definition : Interpolation and Extrapolation
(a) Newton Forward Interpolation Formula
2 3 4
0 0 0 0 0
0
1 0 2 1 1
( 1) ( 1)( 2) ( 1)( 2)( 3)
( ) ...
2 ! 3 ! 4 !
W h e r e , ...
n
n n
p p p p p p p p p
P x y p y y y y
x x
p h x x x x x x
h

     
         

       
Interpolation for equal intervals

19. E x -1 : U s in g N e w t o n F o r w a r d In t e r p o la t io n F o r m u la f in d
(1 .6 ) f r o m t h e f o llo w in g t a b u la r v a lu e s .
1 1 .4 1 .8 2 .2
( ) 3 .4 9 4 .8 2 5 .9 6 6 .5
f
x
y f x
Semester :III
Mr. Tushar J Bhatt
Subject : NT
Code :18SAHMT301
Unit No. :2
Topic : N-F-I-F
19
Numerical Techniques
2 3
0 0 0 0
0
1 0 2 1 1
( 1) ( 1)( 2)
( ) .......... (1)
2 ! 3 !
W h e r e , ...
n
n n
p p p p p
P x y p y y y
x x
p h x x x x x x
h

  
        

       
:Solu tion
W e k n o w th a t th e N -F -I-F is g iv e n b y ,
0
0
G iv e n th a t 1, 1 .6 a n d 0 .4
1 .6 1 0 .6 3
1 .5
0 .4 0 .4 2
x x h
x x
T h e r e fo r e p
h
  
 
    
2 3 4
0 0 0 0
In w h ic h w e w a n t t o f in d t h e v a lu e s o f
y , y , y , y , ..... u s in g f o llo w in g t a b le .   

20. Semester :III
Mr. Tushar J Bhatt
Subject : NT
Code :18SAHMT301
Unit No. :2
Topic : N-F-I-F
20
Numerical Techniques
x y 
2

3

0
1x 0
3 .4 9y
1
1 .4x 1
4 .8 2y
2
1 .8x 2
5 .9 6y
3
2 .2x 3
6 .5y
1.33
1.14
0.54
0.19
0.60
0.41
:Solu tion
0 0
2 3
0 0
T h e re fo re 3 .4 9 , 1 .3 3,
0 .1 9 a n d 0 .4 1
S u b s titu te in a b o v e re s u lt ------(1 ) w e g e t,
  
     
y y
y y

21. Semester :III
Mr. Tushar J Bhatt
Subject : NT
Code :18SAHMT301
Unit No. :2
Topic : N-F-I-F
21
Numerical Techniques
2 3
0 0 0 0
( 1) ( 1)( 2)
(1) ( ) ...
2 ! 3 !
n
p p p p p
P x y p y y y
  
        
:Solu tion
1 .5 (1 .5 1) 1 .5 (1 .5 1) (1 .5 2)
( ) 3 .4 9 1 .5 1 .3 3 ( 0 .1 9) ( 0 .4 1)
2 6
n
P x
     
                   
   
( ) 3 .4 9 1 .9 9 5 0 .0 7 1 3 0 .0 2 5 6n
P x                  

22. E x -2 : T h e p o p u la tio n o f th e to w n in d e c e n n ia l c e n s u s w a s a s g iv e n
b e lo w e s tim a te th e p o p u la tio n fo r th e y e a r 1 8 9 5 .
y e a r (x ) 1 8 9 1 1 9 0 1 1 9 1 1 1 9 2 1 1 9 3 1
P o p u la tio n (y ) 4 6 6 6 8 1 9 3 1 0 1
(in th o u s a n d )
Semester :III
Mr. Tushar J Bhatt
Subject : NT
Code :18SAHMT301
Unit No. :2
Topic : N-F-I-F
22
Numerical Techniques
2 3 4
0 0 0 0 0
0
1 0 2 1 1
( 1) ( 1)( 2) ( 1)( 2)( 3)
( ) .......... (1)
2 ! 3 ! 4 !
W h e r e , ...
n
n n
p p p p p p p p p
P x y p y y y y
x x
p h x x x x x x
h

     
         

       
:Solu tion
W e k n o w th a t th e N -F -I-F is g iv e n b y ,

23. Semester :III
Mr. Tushar J Bhatt
Subject : NT
Code :18SAHMT301
Unit No. :2
Topic : N-F-I-F
23
Numerical Techniques
:Solu tion
0
0
G iv e n th a t 1 8 9 1, 1 8 9 5 a n d 1 0
1 8 9 5 1 8 9 1 4
0 .4
1 0 1 0
x x h
x x
T h e r e fo r e p
h
  
 
   
2 3 4
0 0 0 0
In w h ic h w e w a n t t o f in d t h e v a lu e s o f
y , y , y , y , ..... u s in g f o llo w in g t a b le .   

24. x y
1981 46
1901 66
1911 81
1921 93
1931 101
Semester :III
Mr. Tushar J Bhatt
Subject : NT
Code :18SAHMT301
Unit No. :2
Topic : N-F-I-F
24
Numerical Techniques
:Solu tion

2
 3

4

20
15
12
8
-5
-3
-4
2
-1
-3

25. Semester :III
Mr. Tushar J Bhatt
25
Numerical Techniques
:Solu tion
0 0
2 3 4
0 0 0
T h e re fo re 4 6 , 2 0 ,
5 , 2 a n d 3
S u b s titu te in a b o v e re s u lt ------(1 ) w e g e t,
  
       
y y
y y y
2 3 4
0 0 0 0 0
( 1) ( 1)( 2) ( 1)( 2)( 3)
(1) ( )
2 ! 3 ! 4 !
n
p p p p p p p p p
P x y p y y y y
     
         
0 .4 (0 .4 1) 0 .4 (0 .4 1)(0 .4 2)
( ) 4 6 0 .4 2 0 ( 5) (2)
2 6
0 .4 (0 .4 1)(0 .4 2)(0 .4 3)
( 3)
2 4
n
P x
     
              
   
   
   
 
0 .4 ( 0 .6 ) 0 .4 ( 0 .6 )( 1 .6 )
( ) 4 6 0 .4 2 0 ( 5) (2)
2 6
0 .4 ( 0 .6 )( 1 .6 )( 2 .6 )
( 3)
2 4
n
P x
     
              
   
   
   
 

26. Semester :III
Mr. Tushar J Bhatt
Subject : NT
Code :18SAHMT301
Unit No. :2
Topic : N-F-I-F
26
Numerical Techniques
:Solu tion
( ) 4 6 8 0 .6 0 .1 2 8 0 .4 5 1 2n
P x                       

27. E x -3 : D e t e r m in e t h e in t e r p o la t in g p o ly n o m ia l f o r t h e
1 2 3 4
f o llo w in g t a b le o f d a t a :
( ) 1 1 1 5
x
y f x  
Semester :III
Mr. Tushar J Bhatt
Subject : NT
Code :18SAHMT301
Unit No. :2
Topic : N-F-I-F
27
Numerical Techniques
2 3
0 0 0 0
0
1 0 2 1 1
( 1) ( 1)( 2)
( ) .......... (1)
2 ! 3 !
W h e r e , ...
n
n n
p p p p p
P x y p y y y
x x
p h x x x x x x
h

  
        

       
:Solu tion
W e k n o w th a t th e N -F -I-F is g iv e n b y ,
0
0
G iv e n th a t 1, a n d 1
1
1
1
x x x h
x x x
T h e r e fo r e p x
h
  
 
   
2 3 4
0 0 0 0
In w h ic h w e w a n t t o f in d t h e v a lu e s o f
y , y , y , y , ..... u s in g f o llo w in g t a b le .   

28. x y
1 -1
2 -1
3 1
4 5
Semester :III
Mr. Tushar J Bhatt
Subject : NT
Code :18SAHMT301
Unit No. :2
Topic : N-F-I-F
28
Numerical Techniques
:Solu tion

2
 3

0
2
4
2
2
0

29. Semester :III
Mr. Tushar J Bhatt
29
Numerical Techniques
:Solu tion
2 3
0 0 0 0
T h e re fo re 1, 0 , 2 , 0
S u b s titu te in a b o v e re s u lt ------(1 ) w e g e t,
       y y y y
2 3
0 0 0 0
( 1) ( 1)( 2)
(1) ( )
2 ! 3 !
n
p p p p p
P x y p y y y
  
       
( 1)( 2) ( 1)( 2)( 3)
( ) 1 ( 1) (0 ) (2) (0 )
2 6
n
x x x x x
P x x
       
               
   
2
( ) 1 0 3 2 0n
P x x x       

30. Semester :III
Mr. Tushar J Bhatt
30
Numerical Techniques
2 3
4
( 1) ( 1) ( 2)
( )
2 ! 3 !
( 1) ( 2)( 3)
...
4 !
n n n n n
n
p p p p p
P x y p y y y
p p p p
y
  
      
  
  
(b) Newton Backward Interpolation Formula
1 0 1
W h e re , ... , 1 1
n
n n
x x
p h x x x x p
h


        

31. Semester :III
Mr. Tushar J Bhatt
31
Numerical Techniques
2 3
4
( 1) ( 1) ( 2)
( )
2 ! 3 !
( 1) ( 2)( 3)
... (1)
4 !
n n n n n
n
p p p p p
P x y p y y y
p p p p
y
  
      
  
       
E x -1 : C o m p u t e t h e v a lu e o f (7 .5), b y u s i n g s u it a b le in t e r p o la t io n
f o r m u la u s in g t h e f o llo w in g d a t a :
3 4 5 6 7 8
( ) 2 8 6 5 1 2 6 2 1 7 3 4 4 5 1 3
f
x
y f x
:Solu tion
W e k n o w th a t th e N -B -I-F is g iv e n b y ,
G iv e n th a t 8, 7 .5 a n d 1
7 .5 8
0 .5
1
n
n
x x h
x x
T h e r e fo r e p
h
  
 
   
2 3 4
In w h ic h w e w a n t t o f in d t h e v a lu e s o f
y , y , y , y , ..... u s in g f o llo w in g t a b le .n n n n
   

32. x y
3 28
4 65
5 126
6 217
7 344
8 513
Semester :III
Mr. Tushar J Bhatt
Subject : NT
Code :18SAHMT301
Unit No. :2
Topic : N-F-I-F
32
Numerical Techniques
:Solu tion
37
61
91
127
169
24
30
36
42
6
6
6
0
0
0

2

3

4
 5


33. Semester :III
Mr. Tushar J Bhatt
33
Numerical Techniques
:Solu tion
2 3
4 5
T h e re fo re 5 1 3, 1 6 9 , 4 2 , 6 ,
0 , 0
S u b s titu te in a b o v e re s u lt ------(1 ) w e g e t,
      
   
n n n n
n n
y y y y
y y
2 3 4( 1) ( 1) ( 2) ( 1) ( 2)( 3)
(1) ( ) ...
2 ! 3 ! 4 !
n n n n n n
p p p p p p p p p
P x y p y y y y
     
          
( 0 .5) ( 0 .5 1) ( 0 .5) ( 0 .5 1) ( 0 .5 2)
( ) 5 1 3 ( 0 .5) (1 6 9) (4 2) (6 )
2 6
n
P x
          
                  
   
( ) 5 1 3 8 4 .5 5 .2 5 0 .3 7 5n
P x                  

34. Semester :III
Mr. Tushar J Bhatt
34
Numerical Techniques
2 3
4
( 1) ( 1) ( 2)
( )
2 ! 3 !
( 1) ( 2)( 3)
... (1)
4 !
n n n n n
n
p p p p p
P x y p y y y
p p p p
y
  
      
  
       
E x -2 : P o p u la t io n o f a t o w n in t h e c e n s u s is a s g iv e n in t h e d a t a .
E s t im a t e t h e p o p u la t io n in t h e y e a r 1 9 9 6 .
( ) 1 9 6 1 1 9 7 1 1 9 8 1 1 9 9 1 2 0 0 1
P o p u la t io n ( ) 4 6 6 6 8 1 9 3 1 0 1
(in t h o u s a n d s)
Y e a r x
y
:Solu tion
W e k n o w th a t th e N -B -I-F is g iv e n b y ,
G iv e n th a t 2 0 0 1, 1 9 9 6 a n d 1 0
1 9 9 6 2 0 0 1
0 .5
1 0
n
n
x x h
x x
T h e r e fo r e p
h
  
 
   
2 3 4
In w h ic h w e w a n t t o f in d t h e v a lu e s o f
y , y , y , y , ..... u s in g f o llo w in g t a b le .n n n n
   

35. x y
1961 46
1971 66
1981 81
1991 93
2001 101
Semester :III
Mr. Tushar J Bhatt
Subject : NT
Code :18SAHMT301
Unit No. :2
Topic : N-F-I-F
35
Numerical Techniques
:Solu tion
20
15
12
8
-5
-3
-4
2
-1
-3

2

3

4


36. Semester :III
Mr. Tushar J Bhatt
36
Numerical Techniques
:Solu tion
2 3
4
T h e re fo re 1 0 1, 8, 4 , 1,
3
S u b s titu te in a b o v e re s u lt ------(1 ) w e g e t,
        
  
n n n n
n
y y y y
y
2 3 4( 1) ( 1) ( 2) ( 1) ( 2)( 3)
(1) ( ) ...
2 ! 3 ! 4 !
n n n n n n
p p p p p p p p p
P x y p y y y y
     
          
( 0 .5) ( 0 .5 1) ( 0 .5) ( 0 .5 1) ( 0 .5 2)
( ) 1 0 1 ( 0 .5) (8 ) ( 4 ) ( 1)
2 6
( 0 .5) ( 0 .5 1) ( 0 .5 2)( 0 .5 3)
( 3)
2 4
n
P x
          
                    
   
       
   
 
( ) 1 0 1 4 .0 0 .5 0 .0 6 2 5 0 .1 1 7 2n
P x                       

37. Semester :III
Mr. Tushar J Bhatt
37
Numerical Techniques
(c) Gauss’s Forward Interpolation Formula
2 3 4
0 0 1 1 2
( 1) ( 1) ( 1) ( 1) ( 1)( 2)
....
2 ! 3! 4 !
p
p p p p p p p p p
y y p y y y y  
     
         
x y 
2

3

4

2
x 
1
x 
0
x
1
x
2
x
2
y 
1
y 
0
y
1
y
2
y
0
y
1
y
1
y 

2
y 

2
0
y
2
1
y 

2
2
y 

3
1
y 

3
2
y 

4
2
y 

0
1 0 1
W h ere ,
in w h ich ... .n n
x x
p
h
h x x x x 


    

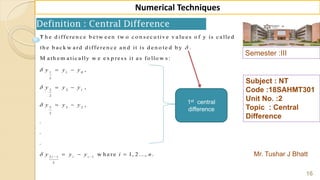
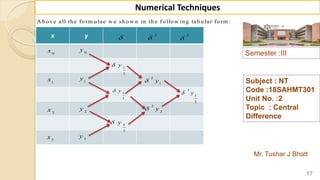
38. Semester :III
Mr. Tushar J Bhatt
38
Numerical Techniques
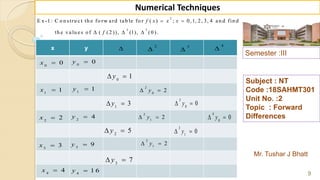
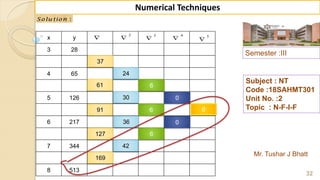
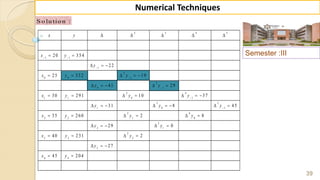
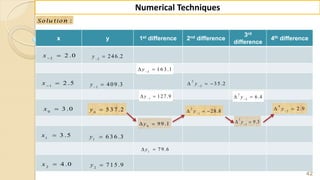
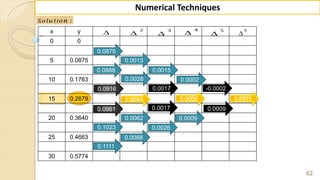
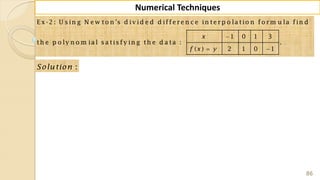
E x -1 : F in d ( 2 2 ) fro m th e fo llo w in g ta b u la r v a lu e s u sin g
G a u ss's fo rw a rd fo rm u la .
2 0 2 5 3 0 3 5 4 0 4 5
3 5 4 3 3 2 2 9 1 2 6 0 2 3 1 2 0 4
f
x
y
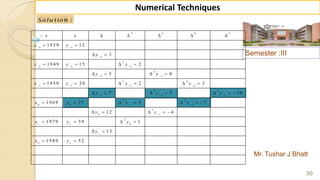
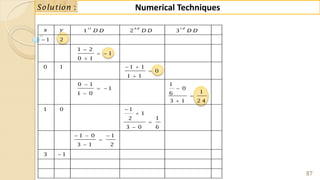
S o lu tio n :
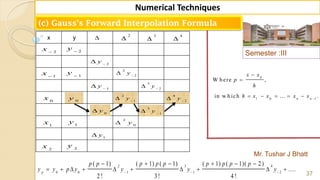
W e k n o w th a t th e G -F -I-F is g iv e n b y ,
2 3 4
0 0 1 1 2
( 1) ( 1) ( 1) ( 1) ( 1)( 2)
....
2 ! 3! 4 !
p
p p p p p p p p p
y y p y y y y  
     
         
1
 

  
    
0
0
H e re w e w a n t to fin d ( ) w h e re 2 2, S o 2 2 is lie s in th e in te rv a l [2 5, 3 0 ] ,
in w h ic h 2 2 is v e ry n e a r to 2 5 ra th e r th a n 3 0 th e re fo re w e c h o o s e 2 5 .
2 2 2 5 3
0 .6
5 5
f x x x
x
x x
p
h

39. 2 3 4 5
1 1
1
2
0 0 1
3
0 1
2 4
1 1 0 1
3 5
1 0 1
2 4
2 2 1 0
3
2 1
2
3 3 2
3
4 4
20 354
22
25 332 19
41 29
30 291 10 37
31 8 45
35 260 2 8
29 0
40 231 2
27
45 204
x y
x y
y
x y y
y y
x y y y
y y y
x y y y
y y
x y y
y
x y
 





    
 
  
    
    
      
       
     
    
   
  
 
Semester :III
39
Numerical Techniques
S o lu tio n :

40. Semester :III
40
Numerical Techniques
S o lu tio n : W e have substitute the values of
2 3 4
0 0 1 1 2
( 1) ( 1) ( 1) ( 1) ( 1)( 2)
....
2 ! 3! 4 !
p
p p p p p p p p p
y y p y y y y  
     
         
1
  0 .6A n d p
in th e fo llo w in g eq u atio n ......(1 ) w e g et
( 0.6)( 0.6 1) ( 0.6 1)( 0.6)( 0.6 1)
(1) 332 ( 0.6)( 41) ( 19) (29)
2 6
p
y
       
         
( 0.6)( 0.6 1) ( 0.6 1)( 0.6)( 0.6 1)
332 ( 0.6)( 41) ( 19) (29)
2 6
332 24.6 9.12 1.856
349.336
p
p
p
y
y
y
       
         
    
 

41. Semester :III
41
Numerical Techniques
1 0 1
0
W h e r e ,
... 0 .5
3 .2 3 .0 0 .2
0 .4
0 .5 0 .5
n n
h x x x x
x x
p
h

     
 
   
E x -2 : F in d t h e v a lu e s o f y w h e n x = 3 .2 f r o m t h e f o llo w in g d a t a
u s in g G a u s s 's f o r w a r d in t e r p o la t io n f o r m u la :
2 .0 2 .5 3 .0 3 .5 4 .0
2 4 6 .2 4 0 9 .3 5 3 7 .2 6 3 6 .3 7 1 5 .9
x
y
:Solu tion
W e k n o w th a t th e G -F -I-F is g iv e n b y ,
2 3 4
0 0 1 1 2
( 1) ( 1) ( 1) ( 1) ( 1)(p 2)
( ) ...
2 ! 3 ! 4 !
n
p p p p p p p p
P x y p y y y y  
     
         
1

42. 42
Numerical Techniques
1
x y 1st difference 2nd difference
3rd
difference
4th difference
2
2 .0
x
1
2 .5
x
0
3 .0x
1
3 .5x
2
4 .0x
0
5 3 7 .2y
1
409.3
y
2
246.2
y
1
6 3 6 .3y
2
7 1 5 .9y
0
9 9 .1 y
1
7 9 .6 y
1
127.9
 y
2
1 6 3 .1
 y
2
1
28.8
  y
2
2
35.2
  y
3
1
9.3
 y
3
2
6.4
 y
4
2
2.9
 y
:Solu tion

43. 43
Numerical Techniques
:Solu tion
N o w w e h a v e 0 .4 a n dp
2 3 4
0 0 1 1 2
( 1) ( 1) ( 1) ( 1) ( 1)(p 2)
(1) ( ) ...
2 ! 3 ! 4 !
n
p p p p p p p p
P x y p y y y y  
     
          
   
0 .4 (0 .4 1)
( ) 5 3 7 .2 0 .4 9 9 .1 2 8 .8
2
(0 .4 1) (0 .4 ) (0 .4 1) (0 .4 1) (0 .4 ) (0 .4 1) (0 .4 2)
9 .3 2 .9
6 2 4
n
P x
  
                
  
          
             
      
         ( ) 5 3 7 .2 3 9 .6 4 3 .4 5 6 0 .5 2 0 8 0 .0 6 4 9 6n
P x     
( ) 5 7 9 .8 4n
P x  ANSWER
S ubstitute all the above values in result ..............(1) w e get

44. Semester :III
Mr. Tushar J Bhatt
44
Numerical Techniques
(d) Gauss’s Backward Interpolation Formula
2 3 4
0 1 1 2 2
( 1) ( 1) ( 1) ( 1) ( 1)( 2)
....
2 ! 3! 4 !
p
p p p p p p p p p
y y p y y y y   
     
         
x y 
2

3

4

2
x 
1
x 
0
x
1
x
2
x
2
y 
1
y 
0
y
1
y
2
y
0
y
1
y
1
y 

2
y 

2
0
y
2
1
y 

2
2
y 

3
1
y 

3
2
y 

4
2
y 

0
1 0 1
W h ere ,
in w h ich ... .n n
x x
p
h
h x x x x 


    

45. Semester :III
Mr. Tushar J Bhatt
45
Numerical Techniques
E x -1 : U s in g G a u s s 's b a c k w a rd in te rp o la ti o n fo rm u la fin d (8 ) fro m th e
0 5 1 0 1 5 2 0 2 5
fo llo w in g ta b le .
7 1 1 1 4 1 8 2 4 3 2
y
x
y
:Solu tion
W e k n o w th a t th e G -B -I-F is g iv e n b y ,
2 3 4
0 1 1 2 2
( 1) ( 1) ( 1) ( 1) ( 1)( 2)
....
2 ! 3! 4 !
p
p p p p p p p p p
y y p y y y y   
     
         
1 0 1
0
0
W h ere ... 5, an d 8 is n ear to th e tab u lar valu e 1 0
th erefo re 1 0 .
8 1 0 2
In w h ich 0 .4
5 5
n n
h x x x x x
x
x x
p
h

      

  
    
1

46. 2 3 4 5
2 2
2
2
1 1 2
3
1 2
2 4
0 0 1 2
3 5
0 1 2
2 4
1 1 0 1
3
1 0
2
2 2 1
2
3 3
0 7
4
5 1 1 1
3 2
1 0 1 4 1 1
4 1 0
1 5 1 8 2 1
6 0
2 0 2 4 2
8
2 5 3 2
x y
x y
y
x y y
y y
x y y y
y y y
x y y y
y y
x y y
y
x y
 

  
 
 
 

    
 
 
    
   
      
     
      
   
   
 
 
Semester :III
Mr. Tushar J Bhatt
46
Numerical Techniques
:Solu tion :Solu tion

47. Semester :III
Mr. Tushar J Bhatt
47
Numerical Techniques
:Solu tion :Solu tion
 N o w w e h a v e 0 .4 a n dp
S ubstitute all the above values in result ..............(1) w e get
2 3 4
0 1 1 2 2
( 1) ( 1) ( 1) ( 1) ( 1)( 2)
(1) ....
2 ! 3! 4 !
p
p p p p p p p p p
y y p y y y y   
     
          

48. Semester :III
Mr. Tushar J Bhatt
48
Numerical Techniques
:Solu tion :Solu tion
( 0 .4 )( 0 .4 1)
(1) 1 4 ( 0 .4 ) (3) (1)
2
( 0 .4 1)( 0 .4 )( 0 .4 1)
( 2 )
6
( 0 .4 1)( 0 .4 )( 0 .4 1)( 0 .4 2 )
( 1)
2 4
p
y
  
      
    
 
      
  
1 4 1 .2 0 .1 2 0 .1 1 2 0 .0 3 4
1 2 .8 2 6
p
p
y
y
     
 

49. Semester :III
Mr. Tushar J Bhatt
49
Numerical Techniques
E x -2 : U s in g G a u s s 's b a c k w a rd in te rp o la ti o n fo rm u la fin d (1 9 7 4 ) fro m th e
1 9 3 9 1 9 4 9 1 9 5 9 1 9 6 9 1 9 7 9 1 9 8 9
fo llo w in g ta b le .
1 2 1 5 2 0 2 7 3 9 5 2
y
x
y
:Solu tion
W e k n o w th a t th e G -B -I-F is g iv e n b y ,
2 3 4
0 1 1 2 2
( 1) ( 1) ( 1) ( 1) ( 1)( 2)
....
2 ! 3! 4 !
p
p p p p p p p p p
y y p y y y y   
     
         
1 0 1
0
0
W h ere ... 1 0, an d 1 9 7 4 is n ear to th e tab u lar valu e 1 9 6 9
th erefo re 1 9 6 9 .
1 9 7 4 1 9 6 9 5
In w h ich 0 .5
1 0 1 0
n n
h x x x x x
x
x x
p
h

      

 
   
1

50. Semester :III
Mr. Tushar J Bhatt
50
Numerical Techniques
:Solu tion
2 3 4 5
3 3
3
2
2 2 3
3
2 3
2 4
1 1 2 3
3 5
1 2 3
2 4
0 0 1 2
3
0 1
2
1 1 0
1
2 2
1 9 3 9 1 2
3
1 9 4 9 1 5 2
5 0
1 9 5 9 2 0 2 3
7 3 1 0
1 9 6 9 2 7 5 7
1 2 4
1 9 7 9 3 9 1
1 3
1 9 8 9 5 2
x y
x y
y
x y y
y y
x y y y
y y y
x y y y
y y
x y y
y
x y
 

  
 
   
  
 

    
 
 
   
   
     
      
      
    
   
 
 

51. Semester :III
Mr. Tushar J Bhatt
51
Numerical Techniques
:Solu tion :Solu tion
N o w w e h a v e 0 .5 a n dp
S ubstitute all the above values in result ..............(1) w e get
2 3 4
0 1 1 2 2
5
3
( 1) ( 1) ( 1) ( 1) ( 1)( 2 )
(1)
2 ! 3 ! 4 !
( 1) ( 1)( 2 )( 2 )
5 !
p
p p p p p p p p p
y y p y y y y
p p p p p
y
   

     
         
   
 

52. Semester :III
Mr. Tushar J Bhatt
52
Numerical Techniques
:Solu tion :Solu tion
(0 .5 )(0 .5 1) (0 .5 1)(0 .5 )(0 .5 1)
(1) 2 7 (0 .5 )(7 ) (5 ) (3)
2 6
(0 .5 1)(0 .5 )(0 .5 1)(0 .5 2 )
( 7 )
2 4
(0 .5 1)(0 .5 )(0 .5 1)(0 .5 2 )(0 .5 2 )
( 1 0 )
1 2 0
p
y
  
      
  
  
   
  
      
 
2 7 3 .5 1 .8 7 5 0 .1 8 7 5 0 .2 7 4 3 0 .1 1 7 2
3 2 .5 3 2
p
p
y
y

53. Semester :III
Mr. Tushar J Bhatt
53
Numerical Techniques
:Solu tion :Solu tion
      
 
2 7 3 .5 1 .8 7 5 0 .1 8 7 5 0 .2 7 4 3 0 .1 1 7 2
3 2 .5 3 2
p
p
y
y

54. Semester :III
Mr. Tushar J Bhatt
54
Numerical Techniques
(c) Stirling’s Interpolation Formula
 We have discussed Newton forward and backward
interpolation formulae which are applicable for interpolation
near the beginning and end respectively, of tabulated values.
 They are not suited to estimate the value of a function near
the middle of a table.
 To obtain more accuracy near the middle of a table, we use
central difference interpolation formulae.

55. Semester :III
Mr. Tushar J Bhatt
55
Numerical Techniques
(c) Stirling’s Interpolation Formula
x y
1st
difference
2nd
difference
3rd
difference
4th
difference
2
x
1
x
0
x
1
x
2
x
0
y
1
y
2
y
1
y
2
y
0
 y
1
 y
1
 y
2
 y
2
0
 y
2
1
 y
2
2
 y
3
1
 y
3
2
 y
4
2
 y

56. Mr. Tushar J Bhatt
56
Numerical Techniques
(c) Stirling’s Interpolation Formula
3 32 2 2 2
2 40 1 1 2
0 1 2
5 52 2 2 2 2
62 3
3
( 1) ( 1)
2 2 ! 3 ! 2 4 !
( 1)( 4 ) ( 1)( 4 )
...
5 ! 2 6 !
p
y y y yp p p p p
y y p y y
y yp p p p p p
y
  
 
 

         
         
  
      
    
 
0
1 0 1
W h e r e , ... n n
x x
p h x x x x
h


     
1 1
In u s in g t h is f o r m u la , w e s h o u ld h a v e < .
2 2
1 1
G o o d e s t im a t e s w ill b e o b t a in e d if < .
4 4
p
p





57. Semester :III
Mr. Tushar J Bhatt
57
Numerical Techniques
1 2 .2
E x -1 : U sin g S tirlin g 's fo rm u la to co m p u t e fro m th e fo llo w in g tab le
1 0 1 1 1 2 1 3 1 4
0 .2 3 9 6 7 0 .2 8 0 6 0 0 .3 1 7 8 8 0 .3 5 2 0 9 0 .3 8 3 6 8
y
x
y
:Solu tion
W e k n o w th a t th e S -C -I-F is g iv e n b y ,
1
3 32 2 2 2
2 40 1 1 2
0 1 2
( 1) ( 1)
...
2 2 ! 3 ! 2 4 !
p
y y y yp p p p p
y y p y y
  
 
         
          
  


     
 
  
0
1 0 1
0
H e r e 1 2 .2 is n e a r t o t h e t a b u la r v a lu e s = 1 2
A n d W h e r e ... 1 ,
1 2 .2 1 2
0 .2
1
n n
x x
h x x x x
x x
p
h

58. 58
Numerical Techniques
x y 1st difference 2nd difference 3rd difference 4th difference
2
1 0x 

1
1 1x 

0
1 2x 
1
1 3x 
2
1 4x 
0
0.31788y 
1
0.28060y

2
0.23967y

1
0.35209y 
2
0.38368y 
0
0 .0 3 4 2 1y 
1
0.03159y 
1
0.03728y
 
2
0.04093y
 
2
0
0.00062y  
2
1
0.00307y
  
2
2
0.00365y
  
3
1
0.00045y
  
3
2
0 .0 0 0 5 8y
 
4
2
0.00013y
  
:Solu tion

59. 59
Numerical Techniques
:Solu tion
N o w w e h a v e 0 .5 a n dp
S ubstitute all the above values in result ..............(1) w e get
  
 
         
           
  
3 32 2 2 2
2 40 1 1 2
0 1 2
( 1) ( 1)
(1) ...
2 2 ! 3 ! 2 4 !
p
y y y yp p p p p
y y p y y

60. 60
Numerical Techniques
:Solu tion
 
       
 
   
    
 
2
2 2 2
0 .0 3 7 2 8 0 .0 3 4 2 1 (0 .2)
(1) 0 .3 1 7 8 8 (0 .2) ( 0 .0 0 3 0 7 )
2 2
(0 .2) ((0 .2) 1) 0 .0 0 0 5 8 0 .0 0 0 4 5 (0 .2) ((0 .2) 1)
( 0 .0 0 0 1 3)
6 2 2 4
p
y
     0 .3 1 7 8 8 0 .0 0 7 1 5 0 .0 0 0 0 6 0 .0 0 0 0 0 2 0 .0 0 0 0 0 0 2p
y
  0 .3 2 4 9 7p
y

61. Semester :III
Mr. Tushar J Bhatt
61
Numerical Techniques
E x -2 : U sin g S tirlin g 's fo rm u la to co m p u t e tan 1 6 fro m th e fo llo w in g tab le
0 5 1 0 1 5 2 0 2 5 3 0
tan 0 0 .0 8 7 5 0 .1 7 6 3 0 .2 6 7 9 0 .3 6 4 0 0 .4 6 6 3 0 .5 7 7 4
x
y x
:Solu tion W e k n o w th a t th e S -C -I-F is g iv e n b y ,
0
1 0 1
0
H e r e 1 6 is n e a r t o t h e t a b u la r v a lu e s = 1 5
A n d W h e r e ... 5 ,
1 6 1 5 1
0 .2
5 5
n n
x x
h x x x x
x x
p
h


     
 
   
3 32 2 2 2
2 40 1 1 2
0 1 2
5 52 2 2 2 2
62 3
3
( 1) ( 1)
2 2 ! 3 ! 2 4 !
( 1)( 4 ) ( 1)( 4 )
... (1)
5 ! 2 6 !
p
y y y yp p p p p
y y p y y
y yp p p p p p
y
  
 
 

         
         
  
      
      
 

62. 62
Numerical Techniques
:Solu tion
x y
0 0
5 0.0875
10 0.1763
15 0.2679
20 0.3640
25 0.4663
30 0.5774

2

3

4
 5

6

0.0875
0.0888
0.0916
0.1023
0.1111
0.0961
0.0013
0.0028
0.0015
0.0062
0.0088
0.0045
0.0017
0.0017
0.0026
0.0002
0.0000
-0.0002
0.0009
0.0009
0.0011

63. 63
Numerical Techniques
:Solu tion
N o w w e h a v e 0 .2 a n dp 
S ubstitute all the above values in result ..............(1) w e get
3 5
2 4 61 2 3
0 1 2 33 3
0 1 2
0 .0 9 1 6 0 .0 0 1 7 0 .0 0 0 2
0 .2 6 7 9 0 .0 0 4 5 0 0 .0 0 1 1
0 .0 9 6 1 0 .0 0 1 7 0 .0 0 0 9
y y y
y y y y
y y y
  
  
 
      
      
     
3 32 2 2 2
2 40 1 1 2
0 1 2
5 52 2 2 2 2
62 3
3
( 1) ( 1)
2 2 ! 3 ! 2 4 !
( 1)( 4 ) ( 1)( 4 )
... (1)
5 ! 2 6 !
p
y y y yp p p p p
y y p y y
y yp p p p p p
y
  
 
 

         
         
  
      
      
 

64. 64
Numerical Techniques
:Solu tion
   
   
   
2
2 2
2 2
2 2
0 .0 9 6 1 0 .0 9 1 6 (0 .2)
(1) 0 .2 6 7 9 (0 .2) (0 .0 0 4 5)
2 2
(0 .2) (0 .2) 1 (0 .2) (0 .2) 10 .0 0 1 7 0 .0 0 1 7
(0 )
6 2 2 4
(0 .2) (0 .2) 1 (0 .2) 4 0 .0 0 0 9 0 .0 0 0 2
1 2 0 2
(0 .2) (0 .2) 1 (0 .2) 4
(0 .0 0 1 1)
7 2 0
p
y
 
      
 
    
    
 
     
   
 
   
 
0 .2 6 7 9 0 .0 1 8 7 7 0 .0 0 0 0 9 0 .0 0 0 0 5 0 0 .0 0 0 0 0 2 0 .0 0 0 0 0 0 2p
y       
0 .2 8 6 7p
y 

65. Semester :III
65
Numerical Techniques
Interpolation for unequal intervals
 The various interpolation formulae derived so far possess the
disadvantage of being applicable only to equally spaced values of an interval.
It is, therefore desirable to develop interpolation formulae for unequally
spaced values of x.
 Therefore we shall study the Lagrange’s interpolation formula.
Lagrange’s interpolation formula
0 1 0 1
0 11 2
0 1
0 1 0 2 0 1 0 1 2 1
0 1
If y = f (x ) t a k e s t h e v a lu e y , , ..., c o r e s s p o n d in g t o , , ..., t h e n
( )( ) ( )( )( ) ( )
( )
( )( ) ( ) ( )( ) ( )
( )( ) (
n n
nn
n n
y y x x x x
x x x x x xx x x x x x
y f x y y
x x x x x x x x x x x x
x x x x x

    
    
     
  

0 1 1
2
2 0 2 1 2 0 1 1
) ( )( ) ( )
...
( )( ) ( ) ( )( ) ( )
n n
n
n n n n n
x x x x x x x
y y
x x x x x x x x x x x x


  
   
     

66. 66
Numerical Techniques
1 : F o r th e g iv e n fo llo w in g ta b u la r v a lu e s e v a lu a te f(9 ),
5 7 1 1 1 3
u s in g L a g ra n g e 's fo rm u la
( ) 1 5 0 3 9 2 1 4 5 2 2 3 6 6
E x
x
y f x


:Solu tion

   
   
0 1 2 3
0 1 2 3
H e r e g iv e n t h a t 9,
5, 7 , 1 1, 1 3 a n d
1 5 0, 3 9 2, 1 4 5 2, 2 3 6 6 .
x
x x x x
y y y y
            
        
               
1 2 3 0 2 3 0 1 3
0 1
0 1 0 2 0 3 1 0 1 2 1 3 2 0 2 1 2 3
W e know that the Lagrange's interp olatio n form ula is,
( )( )( ) ( )( )( ) ( )( )( )
y
( )( )( ) ( )( )( ) ( )( )( )
p
x x x x x x x x x x x x x x x x x x
y y
x x x x x x x x x x x x x x x x x x
    
    
       
0 1 2
2 3
3 0 3 1 3 2
( )( )( )
.....(1)
( )( )( )
subtitute all the above values in equation ....(1) w e get
x x x x x x
y y
x x x x x x
N ow

67. 67
Numerical Techniques
:Solu tion
        
       
        
        
      
        
(9 7 )(9 1 1)(9 1 3) (9 5)(9 1 1)(9 1 3)
(1 ) y 1 5 0 3 9 2
(5 7 )(5 1 1)(5 1 3) (7 5)(7 1 1)(7 1 3)
(9 5)(9 7 )(9 1 3) (9 5)(9 7 )(9 1 1)
1 4 5 2 2 3 6 6
(1 1 5)(1 1 7 )(1 1 1 3) (1 3 5)(1 3 7 )(1 3 1 1)
p
                    
               
                    
2 ( 2) ( 4) 4 ( 2) ( 4) 4 2 ( 4) 4 2 ( 2)
y 1 5 0 3 9 2 1 4 5 2 2 3 6 6
( 2) ( 6) ( 8) 2 ( 4) ( 6) 6 4 ( 2) 8 6 2
p
        
               
       
1 2 2 ( 1)
y 1 5 0 3 9 2 1 4 5 2 2 3 6 6
6 3 3 6
p
       
           
       
1 5 0 7 8 4 9 6 8 2 3 6 6
y
6 3 1 6
p

68. 68
Numerical Techniques
:Solu tion
                   y 2 5 2 6 1 .3 3 9 6 8 3 9 4 .3 3p
 y 8 1 0p
       
           
       
1 5 0 7 8 4 9 6 8 2 3 6 6
y
6 3 1 6
p

69. 69
Numerical Techniques
2 : F o r th e g iv e n fo llo w in g ta b u la r v a lu e s e v a lu a te ( 4 ),
2 3 5 6
u s in g L a g ra n g e 's fo rm u la
( ) 1 5 3 0 4 5 6 0
E x f
x
y f x


:Solu tion

   
   
0 1 2 3
0 1 2 3
H e r e g i v e n t h a t 4 ,
2, 3, 5, 6 a n d
1 5, 3 0, 4 5, 6 0 .
x
x x x x
y y y y
            
        
               
1 2 3 0 2 3 0 1 3
0 1
0 1 0 2 0 3 1 0 1 2 1 3 2 0 2 1 2 3
W e kn o w th at th e Lagran ge's in terp o latio n fo rm u la is,
( )( )( ) ( )( )( ) ( )( )( )
y
( )( )( ) ( )( )( ) ( )( )( )
p
x x x x x x x x x x x x x x x x x x
y y
x x x x x x x x x x x x x x x x x x
    
    
       
0 1 2
2 3
3 0 3 1 3 2
( )( )( )
.....(1)
( )( )( )
su b titu te all th e ab o v e v alu es in eq u atio n ....(1) w e get
x x x x x x
y y
x x x x x x
N ow

70. 70
Numerical Techniques
:Solu tion
        
       
        
        
      
        
(4 3)(4 5)(4 6 ) (4 2)(4 5)(4 6 )
(1 ) y 1 5 3 0
(2 3)(2 5)(2 6 ) (3 2)(3 5)(3 6 )
(4 2)(4 3)(4 6 ) (4 2)(4 3)(4 5)
4 5 6 0
(5 2)(5 3)(5 6 ) (6 2)(6 3)(6 5)
p
            
               
            
(1)( 1)( 2) (2)( 1)( 2) (2)(1)( 2) (2)(1)( 1)
(1 ) y 1 5 3 0 4 5 6 0
( 1)( 3)( 4 ) (1)( 2)( 3) (3)(2)( 1) (4 )(3)(1)
p
       
            
       
5 2 0 3 0 1 0
(1 ) y
2 1 1 1
p

71. 71
Numerical Techniques
:Solu tion
 y 3 7 .5p
                   y 2 .5 2 0 3 0 1 0p
  y 5 0 1 2 .5p

72. Semester :III
72
Numerical Techniques
Inverse Interpolation method
 For unequal intervals if we want to find the value of x corresponding
given y then we will use following Lagrange’s interpolation formula
Lagrange’s inverse interpolation formula
0 1 0 1
0 21 2
0 1
0 1 0 2 0 1 0 1 2 1
0 1
If x = f (y ) t a k e s t h e v a lu e , , ..., c o r e s s p o n d in g t o y , , ..., t h e n
(y )(y ) (y )(y )(y ) (y )
(y )
(y )(y ) (y ) (y )(y ) (y )
(y )(y ) (y
n n
nn
n n
x x x x y y
y y yy y y
x f x x
y y y y y y
y y

    
    
     
  

0 1 1
2
2 0 2 1 2 0 1 1
) (y )(y ) (y )
...
(y )(y ) (y ) (y )(y ) (y )
n n
n
n n n n n
y y y y
x x
y y y y y y


  
   
     

73. 73
Numerical Techniques
1 : F o r th e g iv e n fo llo w in g ta b u la r v a lu e s fin d x c o rre s p o n d in g to y= 1 2 , u s in g
1 .2 2 .1 2 .8 4 .1 4 .9 6 .2
L a g ra n g e 's in v e rs e in te rp o la tio n fo rm u la
4 .2 6 .8 9 .8 1 3 .4 1 5 .5 1 9 .6
E x
x
y
:Solu tion
0 1 2 3 4 5
0 1 2 3 4 5
H e r e g iv e n t h a t y 1 2,
1 .2, 2 .1, 2 .8, 4 .1, 4 .9 , 6 .2 a n d
4 .2, 6 .8, 9 .8, 1 3 .4 , 1 5 .5, 1 9 .6 .
T a k in g y = 1 2 a n d a b o v e a ll t h e v a lu e s in L a g r a n g e 's
in v e r s e in t e r p o la t io n f o r m u la ;
x x x x x x
y y y y y y

     
     

74. 74
Numerical Techniques:Solution
1 2 3 4 5 1 2 3 4 5
0 1
0 1 0 2 0 3 0 4 0 5 1 0 1 2 1 3 1 4 1 5
0 1 3 4 5
2 0 2 1 2 3 2
(y )
(y )(y )(y )(y )(y ) (y )(y )(y )(y )(y )
(y )(y )(y )(y )(y ) (y )(y )(y )(y )(y )
(y )(y )(y )(y )(y )
(y )(y )(y )(y
x f
y y y y y y y y y y
x x
y y y y y y y y y y
y y y y y
y y y

         
   
         
    

   
0 1 2 4 5
2 3
4 2 5 3 0 3 1 3 2 3 4 3 5
0 1 2 3 5 0 1 2 3 4
4
4 0 4 1 4 2 4 3 4 5 5 0 5 1 5
(y )(y )(y )(y )(y )
)(y ) (y )(y )(y )(y )(y )
(y )(y )(y )(y )(y ) (y )(y )(y )(y )(y )
(y )(y )(y )(y )(y ) (y )(y )(y
y y y y y
x x
y y y y y y y
y y y y y y y y y y
x
y y y y y y y
    
  
     
         
  
       
5
2 5 3 5 4
)(y )(y )
x
y y y

 

75. 75
Numerical Techniques:Solution
(y )
(1 2 6 .8 )(1 2 9 .8 )(1 2 1 3 .4 )(1 2 1 5 .5)(1 2 1 9 .6 )
1 .2
(4 .2 6 .8 )(4 .2 9 .8 )(4 .2 1 3 .4 )(4 .2 1 5 .5)(4 .2 1 9 .6 )
(1 2 4 .2)(1 2 9 .8 )(1 2 1 3 .4 )(1 2 1 5 .5)(1 2 1 9 .6 )
2 .1
(6 .8 4 .2)(6 .8 9 .8 )(6 .8 1 3 .4 )(6 .8 1 5 .5)(6 .8 1 9 .6 )
(
x f
    
 
    
    
 
    

1 2 4 .2)(1 2 6 .8 )(1 2 1 3 .4 )(1 2 1 5 .5)(1 2 1 9 .6 )
2 .8
(9 .8 4 .2)(9 .8 6 .8 )(9 .8 1 3 .4 )(9 .8 1 5 .5)(9 .8 1 9 .6 )
(1 2 4 .2)(1 2 6 .8 )(1 2 9 .8 )(1 2 1 5 .5)(1 2 1 9 .6 )
4 .1
(1 3 .4 4 .2)(1 3 .4 6 .8 )(1 3 .4 9 .8 )(1 3 .4 1 5 .5)(1 3 .4 1 9 .6 )
(1 2 4 .
    

    
    
 
    


2)(1 2 6 .8 )(1 2 9 .8 )(1 2 1 3 .4 )(1 2 1 9 .6 )
4 .9
(1 5 .5 4 .2)(1 5 .5 6 .8 )(1 5 .5 9 .8 )(1 5 .5 1 3 .4 )(1 5 .5 1 9 .6 )
(1 2 4 .2)(1 2 6 .8 )(1 2 9 .8 )(1 2 1 3 .4 )(1 2 1 5 .5)
6 .2
(1 9 .6 4 .2)(1 9 .6 6 .8 )(1 9 .6 9 .8 )(1 9 .6 1 3 .4 )(1 9 .6 1 5 .5)
   

    
    
 
    

76. 76
Numerical Techniques
:Solution
0.022 0.234 1.252 3.419 0.964 0.055x      
3.55x 

77. 77
Numerical Techniques
2 : A p p ly L an g ran g es fo rm u la in versely to o b tain a ro o t o f th e eq u atio n
( ) 0, g iven th at (3 0 ) -3 0, (3 4 ) 1 3, (3 8) 3 an d (4 2 ) 1 8 .

     
E x
f x f f f f
:Solu tion
0 1 2 3
0 1 2 3
H e r e g iv e n t h a t y 0,
3 0, 3 4 , 3 8, 4 2 a n d
3 0, 1 3, 3, 1 8 .
T a k in g y = 0 a n d a b o v e a ll t h e v a lu e s in L a g r a n g e 's
in v e r s e in t e r p o la t io n f o r m u la ;
x x x x
y y y y

   
     

78. 78
Numerical Techniques:Solution
1 2 3 0 2 3
0 1
0 1 0 2 0 3 1 0 1 2 1 3
0 1 3 0 1 2
2 3
2 0 2 1 2 3 3 0 3 1 3 2
(y )
(y )(y )(y ) (y )(y )(y )
(y )(y )(y ) (y )(y )(y )
(y )(y )(y ) (y )(y )(y )
(y )(y )(y ) (y )(y )(y )
x f
y y y y y y
x x
y y y y y y
y y y y y y
x x
y y y y y y
 
     
   
     
     
   
     
(0 1 3)(0 3)(0 1 8 ) (0 3 0 )(0 3)(0 1 8 )
3 0 3 4
( 3 0 1 3)( 3 0 3)( 3 0 1 8 ) ( 1 3 3 0 )( 1 3 3)( 1 3 1 8 )
(0 3 0 )(0 1 3)(0 1 8 ) (0 3 0 )(0 1 3)(0 3)
3 8 4 2
(3 3 0 )(3 1 3)(3 1 8 ) (1 8 3 0 )(1 8 1 3)(1 8 3)
x
     
    
           
     
   
     

79. 79
Numerical Techniques
:Solution
(1 3)( 3)( 1 8 ) (3 0 )( 3)( 1 8 )
3 0 3 4
( 1 7 )( 3 3)( 4 8 ) (1 7 )( 1 6 )( 3 1)
(3 0 )(1 3)( 1 8 ) (3 0 )(1 3)( 3)
3 8 4 2
(3 3)(1 6 )( 1 5) (4 8 )(3 1)(1 5)
x
   
    
    
 
   

0.782 6.532 33.682 2.202x     
3 7 .2 3x 

80. 80
Numerical Techniques
N ew ton - D evided D ifference Form ula
0 1
0 1
1 0
0 1
1 0
L e t f (x ) b e g iv e n a t (n + 1 ) d is t in c t p o in t s x , , ..., . W e d e f in e
t h e f ir s t d iv id e d d if f e r e n c e o f f (x ) f o r t h e p o in t s x a n d x a s
( ) ( )
f (x , ) .........(1)
n
x x
f x f x
x
x x



1
0 1 2
1 2 0
0 1 2
2 0
T h e s e c o n d d iv id e d d if f e r e n c e o f f (x ) f o r t h e p o in t s x , x a n d x
is d e f in e a s
( , x ) ( , x )
f (x , , x ) ........(2)
f x f x
x
x x



11 2 0 1
0 1 2
0
a n d in g e n e r a l th e n d iv id e d d if f e r e n c e is d e f in e a s
( , x ,..., x ) ( , x ,...., x )
f (x , , x ,...., x ) ........(3)
th
n n
n
n
f x f x
x
x x





81. 81
Numerical TechniquesDevided Difference Table
0 0
1 0
0 1
1 0
1 1 1 2 0 1
0 1 2
2 0
2 1 1 2 3 0 1 2
1 2 0 1 2 3
2 1 3 0
2 2 2 3 1 2
1 2 3
3 1
( ) 1 2 3
( ) ( )
( , x )
( ) ( , x ) ( , x )
( , x , x )
( ) ( ) ( , x , x ) ( , x , x )
( , x ) ( , x , x , x )
( ) ( , x ) ( , x )
( , x , x )
(
st n d rd
x f x D D D D D D
f x f x
f x
x x
x f x f x f x
f x
x x
f x f x f x f x
f x f x
x x x x
x f x f x f x
f x
x x
f x






 
 
 



3 2
2 3
3 2
3 3
( ) ( )
, x )
( )
f x f x
x x
x f x




82. 82
Numerical Techniques
N ew ton-D evided D ifference Form ula
0 0 0 1 0 1 0 1 2
0 1 2 0 1 2 3
0 1 2 1 0 1 2 3
( ) ( ) (x x ) ( , x ) (x x )(x x ) ( , x , x )
(x x )(x x )(x x ) ( , x , x , x )
.... (x x )(x x )(x x )....(x x ) ( , x , x , x ,..., x )n n
P x f x f x f x
f x
f x
     
   
     
E x -1 : U s in g N e w to n 's d iv id e d d iffe re n c e in te rp o la tio n fo rm u la fin d
1 0 2 5 1 0
f(1 ) a n d f(9 ) fo rm th e fo llo w in g ta b le : .
2 1 7 1 2 4 9 9 9
x
y

 
:Solution

83. 83
Numerical Techniques
:Solu tion
1 2 3 4
1 2
1 2
1
0 1
0 1 4 1
1
2 1
7 1 7 1
4 1
2 0 5 1
2 7 3 9 4 1 1
7 0
5 0 1 0 1
1 2 4 7 1 7 7
3 9 1
5 2 1 0 0
5 1 2 4 1 7 5 3 9
1 7
1 0 2
9 9 9 1 2 4
1 7 5
1 0 5
1 0 9 9 9
s t n d r d th
x y D D D D D D D D
 
 


 


 
 
 
 
 
 
 
 
 







84. 84
Numerical Techniques
:Solu tion
0 0 0 1 0 1 0 1 2
0 1 2 0 1 2 3
0 1 2 1 0 1 2 3
( ) ( ) (x x ) ( , x ) (x x )(x x ) ( , x , x )
(x x )(x x )(x x ) ( , x , x , x )
.... (x x )(x x )(x x )....(x x ) ( , x , x , x ,..., x )n n
P x f x f x f x
f x
f x
     
   
     
( ) 2 (x 1) (1) (x 1)(x 0) (1) (x 1)(x 0)(x 2) (1)P x              
T o fin d : f(1 )
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
(1) (1) 2 (1 1) (1) (1 1)(1 0 ) (1) (1 1)(1 0 )(1 2) (1)
(1) (1) 2 2 2 2
(1) (1) 0
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
f P
f P
f P
               
      
  
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

85. 85
Numerical Techniques
:Solu tion
( ) 2 (x 1) (1) (x 1)(x 0) (1) (x 1)(x 0)(x 2) (1)P x              
T o fin d : f(9 )
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
(9) (9) 2 (9 1) (1) (9 1)(9 0 ) (1) (9 1)(9 0 )(9 2) (1)
(9) (9) 2 1 0 1 1 0 9 1 1 0 9 7 1
(9) (9) 2 1 0 9 0 6 3 0
(9)
f P
f P
f P
f P
               
            
      
  (9) 7 2 8
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _


86. 86
Numerical Techniques
E x -2 : U s in g N e w to n 's d iv id e d d iffe re n c e in te rp o la tio n fo rm u la fin d
1 0 1 3
th e p o ly n o m ia l s a tis fy in g th e d a ta : .
( ) 2 1 0 1
x
f x y

 
:Solution

87. 87
Numerical Techniques:Solution
1 2 3
1 2
1 2
1
0 1
0 1 1 1
0
1 1
0 1 1
1 0
11 0 6
3 1 2 4
1 0 1
1
12
3 0 6
1 0 1
3 1 2
3 1
s t n d r d
x y D D D D D D


 

 



  







  




88. 88
Numerical Techniques:Solution
0 0 0 1 0 1 0 1 2
0 1 2 0 1 2 3
0 1 2 1 0 1 2 3
( ) ( ) (x x ) ( , x ) (x x )(x x ) ( , x , x )
(x x )(x x )(x x ) ( , x , x , x )
.... (x x )(x x )(x x )....(x x ) ( , x , x , x ,..., x )n n
P x f x f x f x
f x
f x
     
   
     
2
3
3
3
3
1
( ) 2 ( x 1) ( 1) ( x 1) ( x 0 ) (0 ) ( x 1) ( x 0 ) ( x 1)
2 4
1
( ) 2 1 0 ( 1)
2 4
1
( ) 2 1 0 ( )
2 4
( ) 2 1 0
2 4 2 4
2 5
( ) 1
2 4 2 4
2 5 2 4
( )
2 4
P x
P x x x x
P x x x x
x x
P x x
x x
P x
x x
P x
             
       
       
      
   
 
 

89. 89
Numerical Techniques
T he O p erators:
 (1) D iffe re n c e O p e ra to rs ( , a n d ) :
(a) T h e F o rw ard d ifferen ce o p erato r is d e n o ted b y , d efin ed as ( ) ( ) ( ).
(b ) T h e B ack w ard d ifferen ce o p erato r is d en o ted b y , d efin ed as ( ) ( ) ( ).
(c ) T h e C en tral d ifferen ce o p erato r i
f x f x h f x
f x f x f x h
    
    
s d en o ted b y , d efin ed as ( )
2 2
W h ere 'h ' is th e d ifferen ce b etw een th e co n secu tive valu es o f th e in d ep en d en t va riab le "x " is called
th e in terval o f d ifferen cin g .
h h
f x f x f x 
   
      
   

90. 90
Numerical Techniques
2
2
2
2
2
2 2
N o w ( ) ( ( ))
( ) ( )
( ) [ ( 1)] ( ......(1))
( ) ( 1) [ ], ( 1 is c o n s ta n t )
( ) ( 1) [ ( 1)] ( ......(1))
( ) ( 1) [ ]..................( 2 )
x x
x x h
x h x h
x h x h
x h x
f x f x
e e
e e e fr o m
e e e e
e e e e fr o m
e e e
   
    
    
     
    
   

  
1
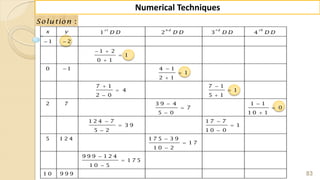
E x -1 : E v a lu a te th e fo llo w in g ( ) ( e ) ( ) (lo g ) ( ) (ta n ).
:
n x
i ii x iii x
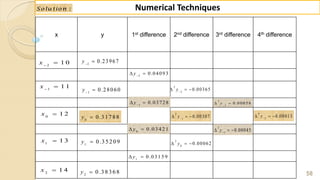
S o lu tio n
H ere w e k n o w th at h e d ifferen tial o p erato r ( ) ( ) ( ).f x f x h f x   
( ) ( ) ( )
x x h x h
i L e t f x e th e r e fo r e f x h e e e

   
( ) ( ) ( )
( ) ( 1).................(1)
x x h x x h
f x f x h f x
e e e e e e
   
     

91. 91
Numerical Techniques
3 2
3 2
3 2
3 2
3 2
3 3
( ) ( ( ))
( ) ( )
( ) [( 1) [ ] ( ......( 2 ))
( ) ( 1) [ ], ( 1 is c o n s ta n t )
( ) ( 1) [ ( 1)] ( ......( 2 ))
( ) ( 1) [ ]..................(3)
x x
x h x
x h x h
x h x h
x h x
S im ila r ly f x f x
e e
e e e fr o m
e e e e
e e e e fr o m
e e e
   
    
    
     
    
   
F ro m resu lt .......(1 ), (2 ) an d (3 ) w e g et in g en eral
( ) ( 1) [ ]
n x h n x
e e e   

92. 92
Numerical Techniques
3 2
3 2
3 2
3 2
3 2
3 3
( ) ( ( ))
( ) ( )
( ) [( 1) [ ] ( ......( 2 ))
( ) ( 1) [ ], ( 1 is c o n s ta n t )
( ) ( 1) [ ( 1)] ( ......( 2 ))
( ) ( 1) [ ]..................(3)
x x
x h x
x h x h
x h x h
x h x
S im ila r ly f x f x
e e
e e e fr o m
e e e e
e e e e fr o m
e e e
   
    
    
     
    
   
F ro m resu lt .......(1 ), (2 ) an d (3 ) w e g et in g en eral
( ) ( 1) [ ]
n x h n x
e e e   

93. 93
Numerical Techniques
( ) ( ) lo g ( ) a n d ( ) lo g ( )
w e k n o w th a t ( ) ( ) - ( )
( ) ( ) ( ) .........(1)
( ) ( ) - ( )
lo g ( ) lo g ( ) lo g ( )
( )
lo g ( ) lo g
( )
( )
lo g ( ) lo g
ii L e t f x f x f x h f x h b u t
f x f x h f x
f x h f x f x
N o w f x f x h f x
f x f x h f x
f x h
f x
f x
f x
f x
   
  
    
  
    
 
    
 
 
  
( )
( .......(1) )
( )
( )
lo g ( ) lo g 1
( )
f x
fr o m
f x
f x
f x
f x
 
 
 
 
    
 

94. 94
Numerical Techniques
1 1
1 1 1
1 1 1 1 1
1 1
( ) ( ) ta n a n d ( ) ta n ( )
( ) ( ) - ( )
ta n ta n ( ) ta n
ta n ta n ta n ta n ta n
1 ( ) 1
ta n ta n
1 ( )
iii L e t f x x f x h x h
N o w f x f x h f x
x x h x
x h x
x
x x h
h
x
x x h
 
 
 
 
  
    
 
   
  
    
      
        
      
 
    
  

95. 95
Numerical Techniques
(2) S h ift O p e ra to r (E ) :
T h e sh ift o p erato r is d en o ted b y E , d efin ed as E ( ) ( ).f x f x h 
2
N o w E ( ) ( ( )) ( ( )) ( ) ( 2 )f x E E f x E f x h f x h h f x h       
3 2
S im ilarly E ( ) ( ( )) ( ( 2 )) ( 2 ) ( 3 )f x E E f x E f x h f x h h f x h       
1
In g e n e ra l E ( ) ( )
E ( ) ( )
E ( ) ( )
n
n
f x f x n h
f x f x h a n d
f x f x n h


  
  
  
R e la tio n b e tw e e n D iffe re n c e o p e ra to r a n d S h ift o p e ra to r
H ere w e k n o w th at h e d ifferen ce o p erato r ( ) ( ) ( )
( ) ( ) ( )
( ) ( 1) ( )
1 1
f x f x h f x
f x E f x f x
f x E f x
E o r E
   
   
   
      

96. 96
Numerical Techniques
(3) D iffe re n tia l O p e ra to r (D ) :
T h e D iffeen tial o p erato r is d en o ted b y D , d efin ed as D ( ) ( ) '( ).
d
f x f x f x
d x
 
2
N o w D ( ) "( )f x f x
3
S im ilarly D ( ) "'( )f x f x
In g en eral D ( ) ( ).
n n
f x f x 
R elatio n b etw een D ifferen tial o p erato r a n d D ifferen ce o p erato r
2 3
2 3
2 3
T a ylo r's se rie s w e h a v e ,
( ) ( ) '( ) "( ) "'( ) ...
2 ! 3 !
( ) ( ) ( ( )) ( ( )) ( ( )) ....
2 ! 3 !
B y
h h
f x h f x h f x f x f x
h h
E f x f x h D f x D f x D f x
     
     

97. 97
Numerical Techniques
R elatio n b etw een D ifferen tial o p erato r a n d D ifferen ce o p erato r
2 2 3 3
2 2 3 3
2 2 3 3
( ) ( ) 1 .....
2 ! 3 !
1 .....
2 ! 3 !
1 .....
2 ! 3 !
1 ( 1 ) .
h D h x
h D
h D h D
E f x f x h D
h D h D
E h D
h x h x
E e e h x
o r e E
 
      
 
     
 
       
 
     

98. 98
Numerical Techniques
(4 ) A v e ra g in g O p e ra to r ( ) :
1
T h e averan g in g o p erato r is d en o ted b y , d efin ed as ( ) .
2 2 2
h h
f x f x f x 
    
       
    
R e la tio n b e tw e e n A v e ra n g in g o p e ra to r a n d S h ift o p e ra to r
 
1 1
2 2
1 1
2 2
1
( )
2 2 2
1
( ) ( ) ( ) ( ) ( )
2
1
2
n
h h
f x f x f x
f x E f x E f x E f x f x n h
E E





    
       
    
 
      
 
 
   
 

99. 99
Numerical Techniques
 


           
1 1 1
1 2 2 2
E x -1 : P ro v e th a t (i) 1 ( ) ( ) ( )E ii E E iii E E iv E
Proof:
W e k n o w th at
( ) ( ) ( )......(1)
( ) ( ) ( )......( 2 )
( ) ......(3)
2 2
f x f x h f x
f x f x f x h
h h
f x f x f x
   
   
   
      
   
E ( ) ( )......( 4 )f x f x h 
1
( ) ......(5 )
2 2 2
h h
f x f x f x
    
       
    

100. 100
Numerical Techniques
 
 
1
1 1
1
1
( ) T o p ro v e : 1
( ) ( ) ( )
( ) ( ) ( ) ( ) ( )
( ) 1 ( )
1 .
i E
f x f x f x h
f x f x E f x E f x f x h
f x E f x
E

 


  
    
     
   
   

101. 101
Numerical Techniques
1 1
2 2
1 1
2 2
1 1
2 2
1 1
2 2
( ) T o p ro v e :
( )
2 2
( ) ( ) ( )
( ) ( )
ii E E
h h
f x f x f x
f x E f x E f x
f x E E f x
E E









 
   
       
   
  
 
   
 
  

102. 102
Numerical Techniques
 
 
   
( ) T o p ro v e : ( )
( ) ( )
( ) ( ) ( )
( ) ( ) ( )
( ) ( ) ( )
( ) ( ) ( )
( ) ( )
iii a E
E f x E f x
E f x E f x f x h
E f x E f x E f x h
E f x f x h f x h h
E f x f x h f x
E f x f x
E
  
   
    
    
      
    
   
   

103. 103
Numerical Techniques
 
 
( ) T o p ro v e : ( )
( ) ( )
( ) ( )
( ) ( ) ( )
( ) ( )
iii b E
E f x E f x
E f x f x h
E f x f x h f x
E f x f x
E
  
  
    
    
   
   

104. 104
Numerical Techniques
1
2
1 1
2 2
1
2
1
2
1
2
1
2
1
2
( ) T o p r o v e :
( ) ( )
( )
2
( )
2 2 2 2
( ) ( ) ( )
( ) ( )
.
iv E
E f x E f x
h
E f x f x
h h h h
E f x f x f x
E f x f x h f x
E f x f x
E

 
 




 
 
   
 
  
    
  
   
         
   
   
  
  

105. 105
Numerical Techniques
   
    
 
         
 
2
1 12 2
2 2 2 2 2
E x -2 : P ro v e th a t ( ) 1 1 ( ) 1 ( ) ( )
2 4 2 2
i ii iii E iv E
Proof:
 
   
 
1 1 1 1
2 2 2 2
1 1 1 1
2 2 2 2
1
2
2 1
2 2 2 1 2
1
( ) W e k n o w th at = an d
2
1
2
1
2
1
2
1
2
4
i E E E E
E E E E
E E
E E
E E E E
 
 
 
 
 
 
 


 
 
   
 
   
      
   
  
 
  
 
 
   

106. 106
Numerical Techniques
 2 2 2 1 2
2 1 2
2 2
2 2
2 2
2
1
2 2
1
1 2 1
4
2 4
1
4
2
1
4
1 ......(1)
2
E E E E
E E E E
E E
E E
 
 
 
 
 
 


     
  
  
 
  
 
    
 
 
2
1 12
2 2
2
1
2 1
2 1
N o w
1
1 1
2 2
1
1 1 2
2 2
2 2
1
2 2
1 ......( 2 )
2 2
E E
E E
E E
E E








 
     
 
     
  
  

  
2
1
2 2
2
2
2 2
F ro m ......(1 ) an d ......(2 ) w e h ave ,
1
2
1 1
2
E E
 

 

 
   
 
 
    
 

107. 107
Numerical Techniques
THANK YOU