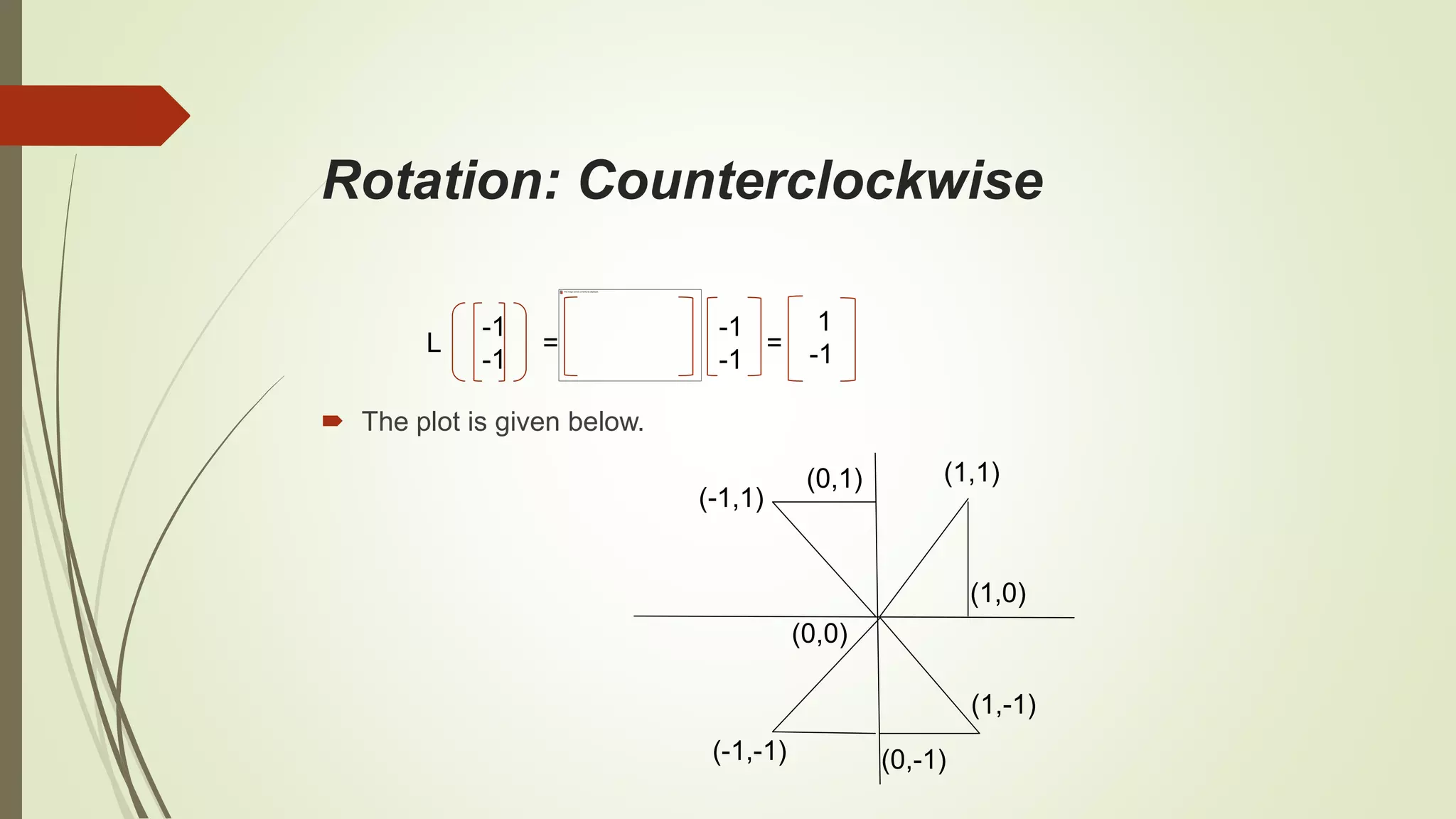
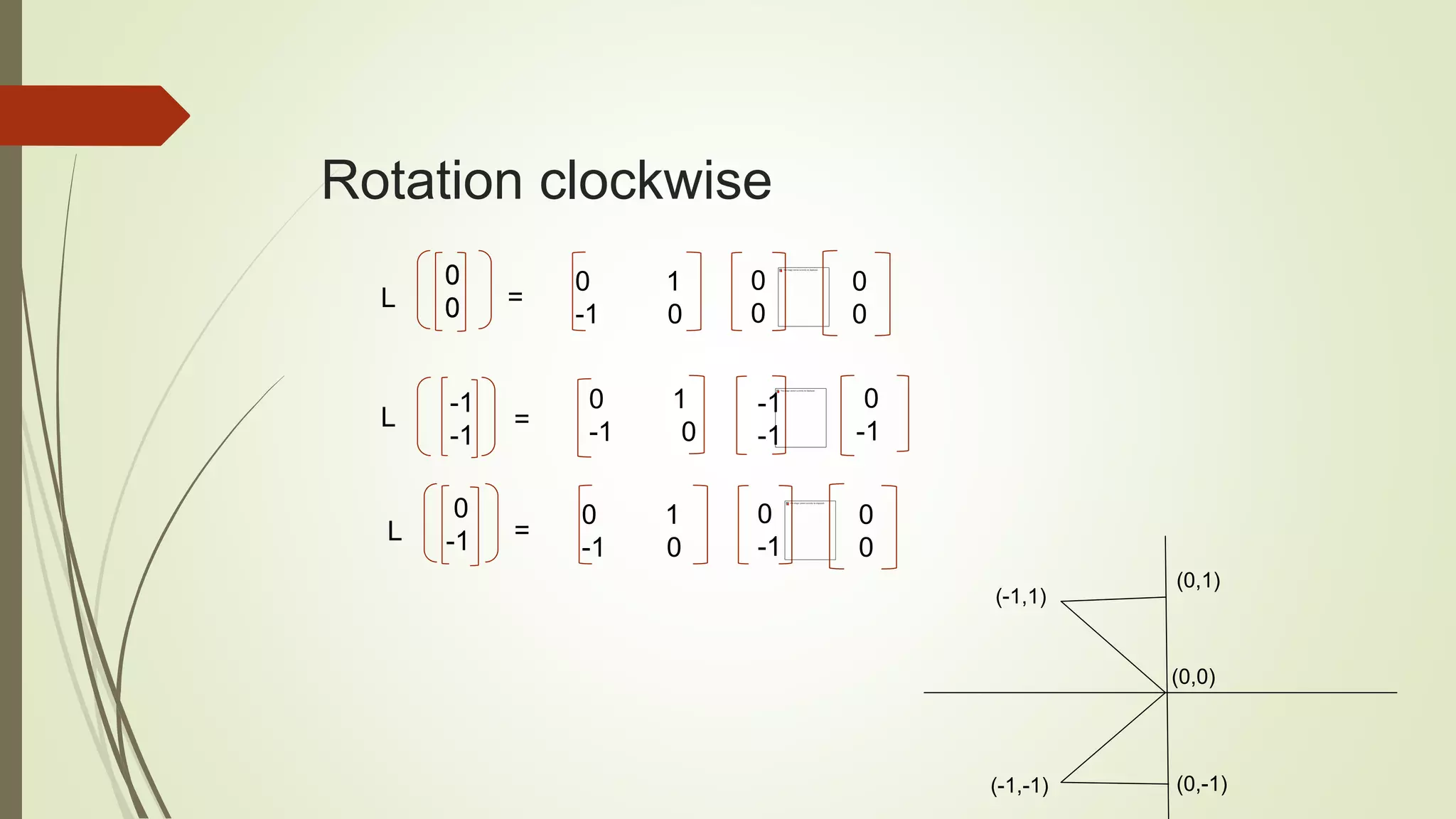
This document discusses linear transformations between vector spaces. It begins by defining a linear transformation as a function between vector spaces that satisfies the properties of vector addition and scalar multiplication. It then provides examples of standard linear transformations like the matrix transformation and zero transformation. The document also covers properties of linear transformations such as how they are determined by the images of basis vectors. Finally, it provides applications of linear operators like reflection, rotation, and shear transformations.

1. G.H.PATEL COLLEGE OF ENGINEERING &
TECHNOLOGY
ANAND
Chapter : 4
Linear Transformations
2110015__150110111041(Shreyans Patel)
150110111042(Smit Patel)
150110111043(Piyush Kabra)
150110111044(Hardik Ramani)
150110111045(Shivam Roy)

2. GENERAL LINEAR TRANSFORMATIONS

3. INTRODUCTION :-
Linear Transformation is a function from one vector space to
another vector space satisfying certain conditions. In
particular, a linear transformation from Rn to Rm is know as
the Euclidean linear transformation . Linear transformation
have important applications in physics, engineering and
various branches of mathematics.

4. Introduction to Linear Transformations
 Function T that maps a vector space V into a vector space W:
V: the domain of T
W: the codomain of T

5. DEFINITION :-
 Let V and W be two vectors spaces. Then a
function T : V W is called a linear transformation from V to W if for all u, U
Ɛ V and all scalars k,
 T(u + v) = T(u) T(v);
 T(ku) = kT(u).
 If V = W, the linear transformation T: V V is called a linear operator on V.

6. PROPERTIES OF LINEAR TRANSFORMATION
:-
Let T : V W be a linear transformation. Then
T(0) = o
T(-v) = -T(u) for all u Ɛ V
T(u-v) = T(u) – T(v) for all u, u Ɛ V
T(k1v1 + k2v2+ ….. +knvn) = k1T(v1) + k2T(v2) + ….. +knT(vn),
Where v1,v2,….vn Ɛ V and k1, k2, …. Kn are scalars.

7. Standard Linear Transformations
 Matrix Transformation: let T : Rn Rm be a linear transformation. Then
there always exists an m × n matrix A such that
T(x) = Ax
 This transformation is called the matrix transformation or the Euclidean linear
transformation. Here A is called the standard matrix for T. It is denoted by [T].
 For example, T : R3 R2 defined by
T(x,y,z) = (x = y-z, 2y = 3z, 3x+2y+5z) is a matrix transformation.

8.  ZERO TRANSFORMATION
 Let V and W be vector spaces.
The mapping T : V W defined by
T(u)
= 0 for all u Ɛ V
 Is called the zero transformation. It is
easy to verify that T is a linear
transformation.
 IDENTITY TRANSFORMATION
 Let V be any vector space.
The mapping I : V V defined by
I(u) = u for all u Ɛ V
 Is called the identity operator on V. it is
for the reader to verify that I is linear.

9. Linear transformation from images of basic vectors
 A linear transformation is completely determined by the images of any set of basis
vectors. Let T : V W be a linear transformation and {v1,v2,……vn} can be
any basis for V. Then the image T(v) of any vector u Ɛ V can be calculated using
the following steps.
 STEP 1: Express u as a linear combination of the basis vectors v1,v2,……,vn,say
V = k1v1 + k2v2+ ….. +knvn.
 STEP 2: Apply the linear transformation T on v as
T(v) = T(k1v1 + k2v2+ ….. +knvn)
T(v) = k1T( v1)+ k2 T(v2)+ ….. +knT(vn)

10. Composition of linear Transformations
 Let T1 : U V and T2 : V W be linear transformation. Then the composition of
T2 with T1 denoted by T2 with T1 is the linear transformation defined by,
(T2 O T1)(u) = T2(T1(u)), where u Ɛ U.
 Suppose that T1 : Rn Rm and T2 : Rm RK are linear transformation. Then
there exist matrics A and B of order m × n and k × m respectively such that
T1(x) = Ax and T2 (x) = Bx
Thus A = [T1] and B = [T2].
Now,
(T2 0 T1)(x) = T2 T1(x) = T2 (Ax) = B(Ax) (BA)(x) = ([T1][T2])(x)

11. So we have
T2 0 T1 = [T2] [T1]
Similarly, for three such linear transformations
T3 0 T2 0 T1 = [T2] [T1][T3]

12.  Ex 1: (A function from R2 into R2 )
(a) Find the image of v=(-1,2). (b) Find the preimage of w=(-1,11)
Sol:
Thus {(3, 4)} is the preimage of w=(-1, 11).

13.  Ex 2: (Verifying a linear transformation T from R2 into R2)
Pf:

14. Therefore, T is a linear transformation.

15. Ex 3: (Functions that are not linear transformations)

16.  Notes: Two uses of the term “linear”.
(1) is called a linear function because its graph is a line.
(2) is not a linear transformation from a vector space R into
R because it preserves neither vector addition nor scalar multiplication.

17.  Ex 4: (Linear transformations and bases)
Let be a linear transformation such that
Sol:
(T is a L.T.)
Find T(2, 3, -2).

18. Applications of Linear
Operators

19.  1. Reflection with respect to x-axis:?
 For example, the reflection for the triangle with vertices is
 The plot is given below.

20. 2. Reflection with respect to y=-x :
 Thus, the reflection for the triangle with vertices (-1,4),(3,1),(2,6) is
 The plot is given below

21. 3. Rotation: Counterclockwise
 For example, as
 Thus, the rotation for the triangle with vertices is

22. Rotation: Counterclockwise
 The plot is given below.

23. Rotation: Counterclockwise
 Thus, the rotation for the triangle with vertices (0,0),(0,1),(-1,1) is
=L
0 -1
1 0
0
0
0
0
0
0
L
0
0
0
1
=
0 -1
1 0
0
1
-1
0

24. Rotation: Counterclockwise
 The plot is given below.
L
-1
1
=
-1
1
=
-1
-1
(-1,1)
(0,1) (1,1)
(0,0)
(-1,-1) (0,-1)
(1,0)

25. Rotation: Counterclockwise
 Thus, the rotation for the triangle with vertices (0,0),(-1,0),(-1,-1) is
=L
0 -1
1 0
0
0
0
0
0
0
L
0
0
-1
0
=
0 -1
1 0
-1
0
0
-1

26. Rotation: Counterclockwise
 The plot is given below.
L
-1
-1
=
-1
-1
=
1
-1
(-1,1)
(0,1) (1,1)
(0,0)
(-1,-1) (0,-1)
(1,-1)
(1,0)

27. Rotation: Counterclockwise

28. Rotation clockwise
 For example, as =180
 Thus, the rotation for the triangle with vertices (0,0),(-1,-1),(0,-1) is
A
0 1
-1 0
Cos180 -Sin180
Sin 180 Cos180

29. Rotation clockwise
=L
0 1
-1 0
0
0
0
0
0
0
L
0
0
-1
-1
=
0 1
-1 0
-1
-1
0
-1
=L
0 1
-1 0
0
-1
0
-1
0
0
(-1,-1)
(0,0)
(0,-1)
(-1,1)
(0,1)

30. Rotation clockwise

31. Shear in the x-direction:
 For example, as ,
 Thus, the shear for the rectangle with vertices in the x-direction is

32. Shear in the x-direction:
 The plot is given below.

33. THANKS