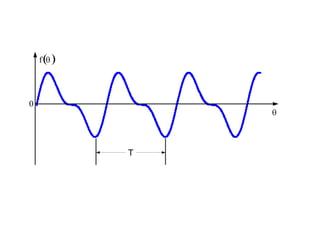
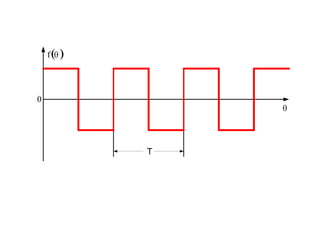
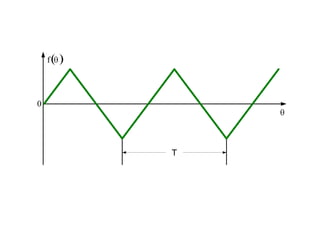
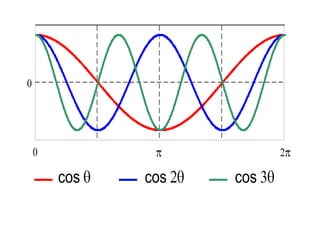
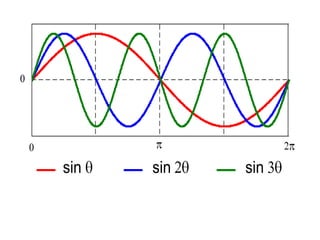
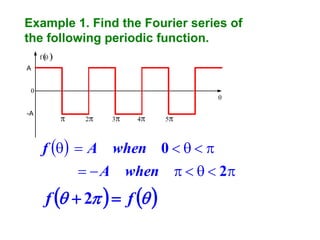
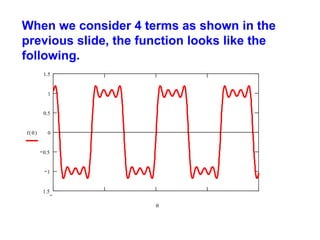
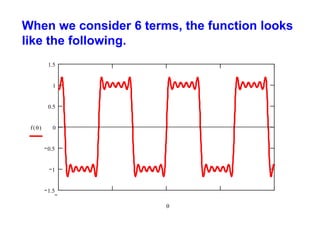
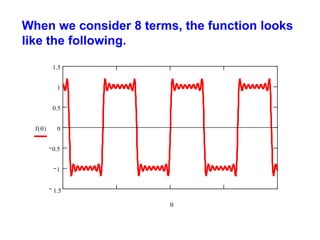
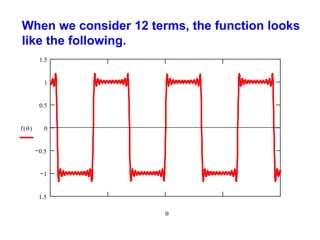
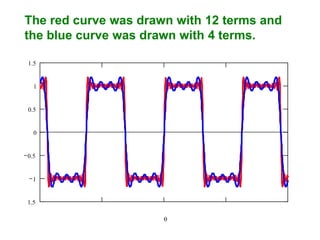
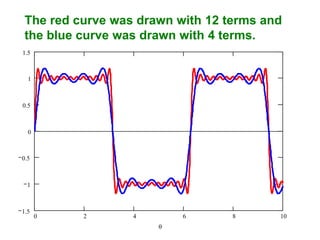
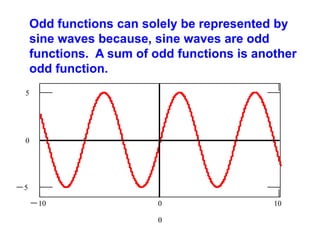
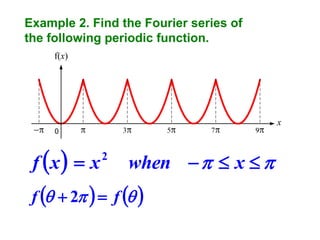
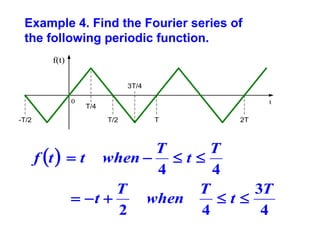
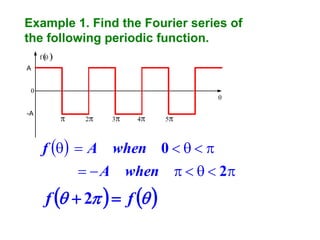
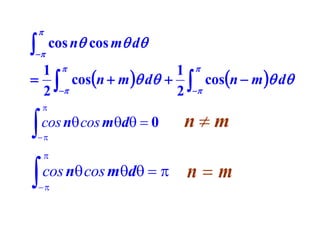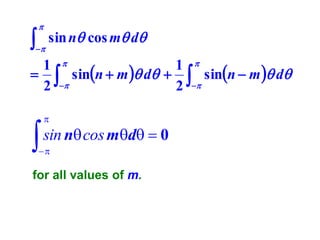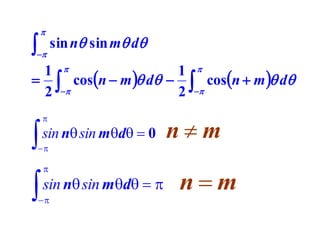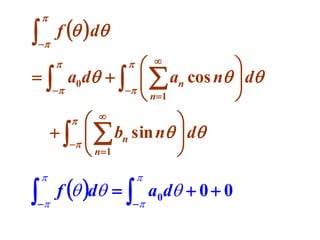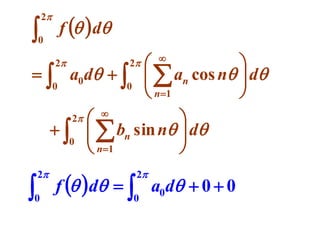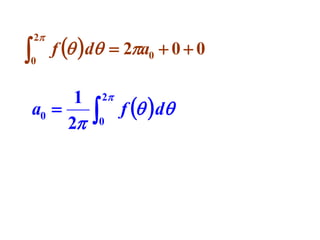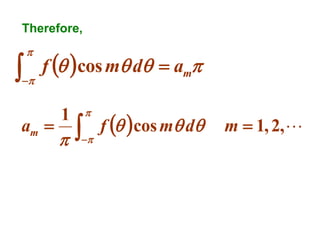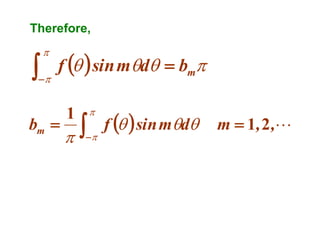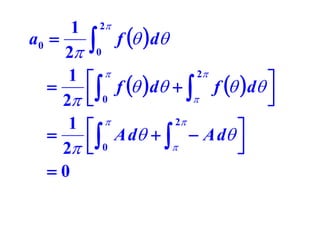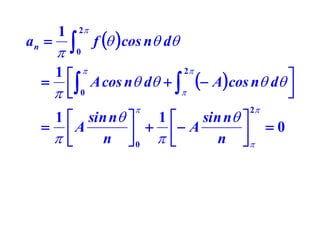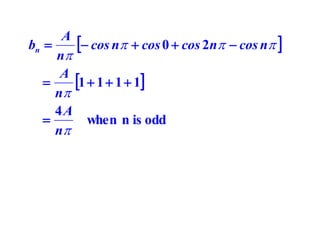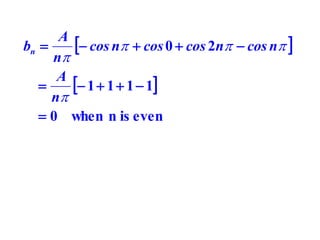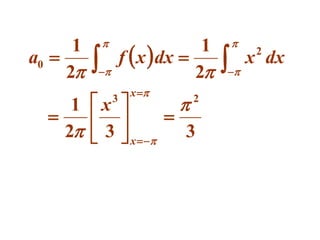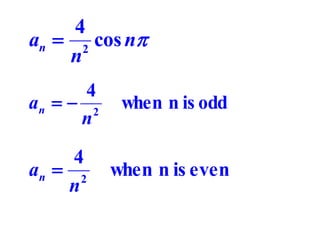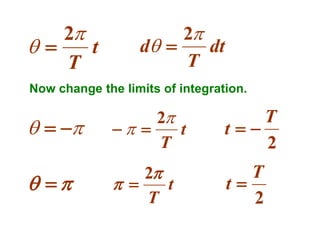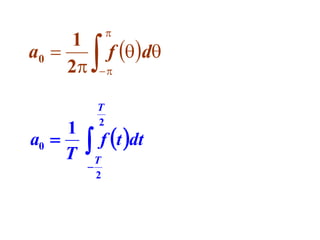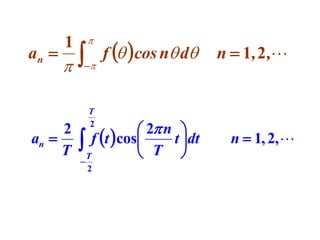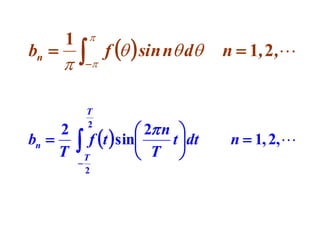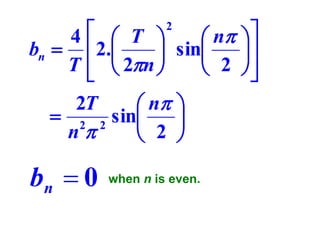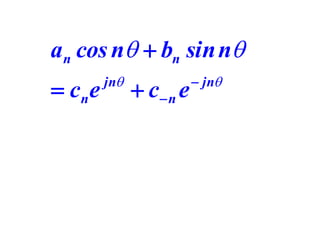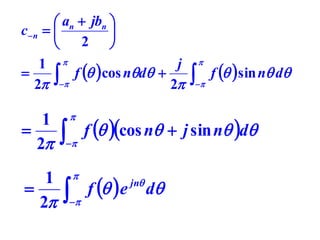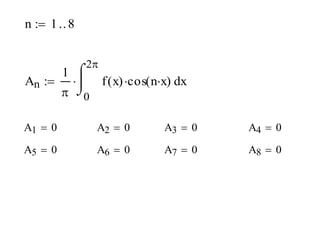This document discusses periodic functions and Fourier series. A periodic function repeats its values over regular intervals called periods. The Fourier series represents periodic functions as the sum of trigonometric functions (sines and cosines) with different frequencies. The document derives the formulas to calculate the coefficients of the Fourier series from a given periodic function. It involves integrating the function multiplied by sines and cosines over one period of the function.

1. Periodic Functions and
Fourier Series

2. Periodic Functions
A function
f  
is periodic
if it is defined for all real

and if there is some positive number,
T
such that
f   T   f   .

3. f
0
T

4. f
0
T

5. f
0
T

6. Fourier Series
f  
be a periodic function with period
2
The function can be represented by
a trigonometric series as:


n 1
n 1
f    a0   an cos n   bn sin n

7. 

n 1
n 1
f    a0   an cos n   bn sin n
What kind of trigonometric (series) functions
are we talking about?
cos  , cos 2 , cos 3  and
sin , sin 2 , sin 3 

8. 0
0
cos
cos
cos

9. 0
0
sin
sin
sin

10. We want to determine the coefficients,
an
and
bn
.
Let us first remember some useful
integrations.

11. 
  cos n cos m d

1 
1 
  cosn  m  d   cosn  m  d
2 
2 


cos n cos md  0
nm



cos n cos md  

nm

12. 
  sin n cos m d

1 
1 
  sinn  m  d   sinn  m  d
2 
2 


sin n cos md  0

for all values of m.

13. 
  sin n sin m d

1 
1 
  cosn  m  d   cosn  m  d
2 
2 


sin n sin md  0



sin n sin md  

nm
nm

14. Determine
a0
Integrate both sides of (1) from

to


  f  d





  a0   an cos n   bn sin n  d

n1
n 1




15. 
  f   d



  a0d     an cos n  d


 
 n 1






    bn sin n  d

 
 n 1





  f  d    a d  0  0


0

16. 

f d  2a0  0  0

1
a0 
2
a0


f d

is the average (dc) value of the
function,
f   .

17. You may integrate both sides of (1) from
0

to
2
instead.
f   d
0

2
2
0


a0   an cos n   bn sin n  d
n 1
n 1




It is alright as long as the integration is
performed over one period.

18. 
2
f   d
0
2
2
0
0
  a0d  

2
0

2
0


  an cos n  d


 n 1




  bn sin n  d


 n 1


2
f   d   a0d  0  0
0

19. 
2
0
f   d  2a0  0  0
1
a0 
2

2
0
f   d

20. Determine
Multiply (1) by
an
cos m
and then Integrate both sides from

to


  f   cos m d





  a0   an cos n   bn sin n  cos m d

n1
n1




21. Let us do the integration on the right-hand-side
one term at a time.
First term,


a0 cos m d  0

Second term,



  n 1
an cos n cos m d

22. Second term,


  a

n
cos n cos m d  am
n1
Third term,


b


n 1
n
sin n cos m d  0

23. Therefore,



f   cos m d  am
am 
1




f   cos m d
m  1, 2, 

24. Determine
Multiply (1) by
bn
sin m
and then Integrate both sides from

to


  f   sin m d





  a0   a n cos n   bn sin n  sin m d

n 1
n 1




25. Let us do the integration on the right-hand-side
one term at a time.
First term,



a0 sin m d  0
Second term,


  a

n 1
n
cos n sin m d

26. Second term,


  a

n 1
n
cos n sin m d  0
Third term,


b


n
n1
sin n sin m d  bm

27. Therefore,



f   sin md  bm
bm 
1




f   sin md
m  1, 2 ,

28. The coefficients are:
1
a0 
2


f d


am 
  f  cos m d

bm 
1
1





f   sin m d
m  1, 2, 
m  1, 2, 

29. We can write n in place of m:
1
a0 
2


f d


an 
  f  cos n d

bn 
1
1





f   sin n d
n  1, 2 ,
n  1, 2 ,

30. The integrations can be performed from
0
to
2
1
a0 
2

2
0
an 

2
bn 
1
2
1
0


0
instead.
f   d
f   cos n d
f   sin n d
n  1, 2 ,
n  1, 2 ,

31. Example 1. Find the Fourier series of
the following periodic function.
f
A
0
-A
f   A when 0    
  A when     2
f   2   f  

32. 1 2
a0 
f   d
0
2
2
1  

f   d   f   d 
 0



2 
2
1  

A d    A d 
 0



2 
0

33. an 
1


2
0
f   cos n d
2
1 

A cos n d    A cos n d 
 0





2
1  sin n 
1
sin n 
 A
    A n   0

n 0



34. bn 
1

2
0
f   sin n d
2
1 

A sin n d    A sin n d 




  0

2
1
cos n 
1  cos n 
  A
 A

n 0  
n 


A
 cos n  cos 0  cos 2n  cos n 

n

35. A
 cos n  cos 0  cos 2n  cos n 
bn 
n
A
1  1  1  1

n
4A

when n is odd
n

36. A
 cos n  cos 0  cos 2n  cos n 
bn 
n
A
 1  1  1  1

n
 0 when n is even

37. Therefore, the corresponding Fourier series is
4A 
1
1
1

 sin  sin 3  sin 5  sin 7  
 
3
5
7

In writing the Fourier series we may not be
able to consider infinite number of terms for
practical reasons. The question therefore, is
– how many terms to consider?

38. When we consider 4 terms as shown in the
previous slide, the function looks like the
following.
1.5
1
0.5
f()
0
0.5
1
1.5


39. When we consider 6 terms, the function looks
like the following.
1.5
1
0.5
f()
0
0.5
1
1.5


40. When we consider 8 terms, the function looks
like the following.
1.5
1
0.5
f ( )
0
0.5
1
1.5


41. When we consider 12 terms, the function looks
like the following.
1.5
1
0.5
f()
0
0.5
1
1.5


42. The red curve was drawn with 12 terms and
the blue curve was drawn with 4 terms.
1.5
1
0.5
0
0.5
1
1.5


43. The red curve was drawn with 12 terms and
the blue curve was drawn with 4 terms.
1.5
1
0.5
0
0.5
1
1.5
0
2
4
6

8
10

44. The red curve was drawn with 20 terms and
the blue curve was drawn with 4 terms.
1.5
1
0.5
0
0.5
1
1.5
0
2
4
6

8
10

45. Even and Odd Functions
(We are not talking about even or
odd numbers.)

46. Even Functions
f(
Mathematically speaking -
f     f  
The value of the
function would
be the same
when we walk
equal distances
along the X-axis
in opposite
directions.

47. Odd Functions
f(
Mathematically speaking -
f      f  
The value of the
function would
change its sign
but with the
same magnitude
when we walk
equal distances
along the X-axis
in opposite
directions.

48. Even functions can solely be represented
by cosine waves because, cosine waves
are even functions. A sum of even
functions is another even function.
5
0
5
10
0

10

49. Odd functions can solely be represented by
sine waves because, sine waves are odd
functions. A sum of odd functions is another
odd function.
5
0
5
10
0

10

50. The Fourier series of an even function f  
is expressed in terms of a cosine series.

f    a0   an cos n
n 1
The Fourier series of an odd function f  
is expressed in terms of a sine series.

f     bn sin n
n 1

51. Example 2. Find the Fourier series of
the following periodic function.
f(x)
x
0
f x   x
2
when    x  
f   2   f  

52. 1
a0 
2
1

2

1
f  x  dx 
2


x 
x 


3
3
  x  
3
2



2
x dx

53. an 
1




f  x  cos nx dx
1  2


x cos nxdx
 



Use integration by parts.

54. 4
an  2 cos n
n
4
an   2
n
4
an  2
n
when n is odd
when n is even

55. This is an even function.
Therefore,
bn  0
The corresponding Fourier series is

cos 2 x cos 3 x cos 4 x


 4 cos x 


 
2
2
2
3
2
3
4


2

56. Functions Having Arbitrary Period
Assume that a function f t  has
period, T . We can relate angle
(  ) with time ( t ) in the following
manner.
  t
 is the angular frequency in radians per
second.

57.   2 f
f is the frequency of the periodic function,
f t 
  2 f t
Therefore,
where
2

t
T
1
f 
T

58. 2

t
T
2
d 
dt
T
Now change the limits of integration.
  
2
 
t
T
T
t
2
 
2

t
T
T
t
2

59. 1
a0 
2
1
a0 
T




f d

T
2
f t dt
T
2

60. an 
1



2
an 
T

T
2
f   cos n d
 2 n 
 Tf t cos T t dt



2
n  1, 2 ,
n  1, 2, 

61. bn 
1

f   sin n d
n  1, 2 ,
 2 n 
 Tf t sin T t dt



n  1, 2, 


2
bn 
T

T
2
2

62. Example 4. Find the Fourier series of
the following periodic function.
f(t)
3T/4
0
-T/2
t
T/4
T/2
T
2T
T
T
f t   t when   t 
4
4
T
T
3T
 t 
when
t
2
4
4

63. f t  T   f t 
This is an odd (periodic) function. Therefore,
an  0
2
 2n 
bn   f t  sin
t dt
T 0
 T 
T
4

T

0
T
2
 2n 
f t  sin
t dt
 T 

64. 4
bn 
T
4

T
T
4
 2n 
t sin
t  dt
 T 
0
T
2
T   2n 

t dt
  t   sin
T 
2  T 
4
Use integration by parts.

65.   T 
 n
 sin
 2.
 2
  2n 

2T
 n 
 2 2 sin

n
 2 
4
bn 
T
bn  0
2
when n is even.





66. Therefore, the Fourier series is
2T
2

  2  1

 6  1
 10 
 sin  T t   2 sin  T t   2 sin  T t   
 3

 5


 


67. The Complex Form of Fourier Series


n 1
n 1
f    a0   an cos n   bn sin n
Let us utilize the Euler formulae.
cos  
sin 
e
e
j
j
e
2
 j
e
2i
 j

68. n
th harmonic component of (1) can be
The
expressed as:
an cos n  bn sin n
 an
 an
e
e
jn
jn
e
2
 jn
e
2
 jn
 bn
e
 ibn
jn
e
e
2i
jn
 jn
e
2
 jn

69. an cos n  bn sin n
 an  jbn  jn  an  jbn   jn

e  
e
2 
2 


Denoting
 a n  jb n
cn  

2

and
c0  a0




,
cn
 a n  jb n 


2



70. an cos n  bn sin n
 cn e
jn
 c n e
 jn

71. The Fourier series for
can be expressed as:


f  
f    c0   cne
n 1


c e
n
n 
jn
jn
 c ne
 jn


72. The coefficients can be evaluated in
the following manner.
 an  jbn 
cn  

2 

1 
j

 f  cos nd  2
2

1

2

1

2





  f  sin n d

f  cos n  j sin n d
f   e
 jn
d

73.  an  jbn 
c n  

2 

1 
j

 f  cos nd  2
2
1

2
1

2


  f  sin n d

  f  cos n  j sin n d


  f   e

jn
d

74.  an  jbn 
cn  

2 

Note that
cn .
cn
 an  jbn 
c n  

 2 
is the complex conjugate of
Hence we may write that
1
cn 
2


f e
 jn
d

.
n  0 ,  1,  2 , 

75. The complex form of the Fourier series of
f   with period
f   
2

c e
n  
n
is:
jn

76. Example 1. Find the Fourier series of
the following periodic function.
f
A
0
-A
f   A when 0    
  A when     2
f   2   f  

77. A  5
f ( x) 
A if 0  x  
A if   x  2 
0 otherwise
2
1 
A0 
 f ( x) dx
2 0
A0  0

78. n  1  8
2
1 
An   f ( x) cos( nx) dx
 0
A1  0
A2  0
A3  0
A4  0
A5  0
A6  0
A7  0
A8  0

79. 2
1 
Bn  
 0
f ( x) sin( nx) dx
B1  6.366
B2  0
B3  2.122
B4  0
B5  1.273
B6  0
B7  0.909
B8  0

80. Comple x Form
f   

c e
1
cn 
2
jn
n
n  


f e  jnd

n  0,  1,  2,
2
1 
C ( n) 

2  0
 1i n  x
f ( x) e
dx

81. 2
1 
C ( n) 

2  0
 1i n  x
f ( x) e
dx
C (0)  0
C (1)  3.183i
C (2)  0
C (3)  1.061i
C (4)  0
C (5)  0.637i
C (6)  0
C (7)  0.455i
C (1)  3.183i
C (2)  0
C (3)  1.061i
C (5)  0.637i
C (6)  0
C (7)  0.455i
C (4)  0