MATLAB is software originally developed as a matrix library that has since added numerical, symbolic, and visualization tools. It allows users to write scripts called m-files to perform calculations and analyze data. Built-in functions include trigonometric, exponential, rounding, and display formatting functions. Plots can be generated by providing x and y data to the plot command. Polynomial roots and solutions to systems of equations can be found. Control structures like for loops are used to iterate calculations.

1. 1
MATLAB Programming

2. 2
MATLAB
a flagship software which was originally developed as a
matrix library. A variety of numerical functions, symbolic
computations, and visualization tools have been added to the
matrix manipulations.
Demo programs:
http://web.mst.edu/~ercal/228/MATLAB/1-2/analpara.m
http://web.mst.edu/~ercal/228/MATLAB/1-2/analpara2.m
http://web.mst.edu/~ercal/228/MATLAB/1-2/analpara4.m
))](([)()( 11 iiiii tttv
m
c
gtvtv  

3. 3
Sample Program
• g=9.8;
• cd=12.5;
• m = 68.1;
• dt = input('time increment (s):');
• tf = input('final time (s):');
• ti=0;
• vi=0;
• while (1)
• dvdt = g-(cd/m)*vi;
• vi = vi + dvdt*dt;
• ti = ti + dt;
• if ti >= tf, break, end
• end
• disp('velocity (m/s):')
• disp(vi)
t (sec.) V (m/s)
0 0
2 19.60
4 32.00
8 44.82
10 47.97
12 49.96
∞ 53.39
m=68.1 kg; c=12.5 kg/s; g=9.8 m/s
))](([)()( 11 iiiii tttv
m
c
gtvtv  

4. 4
Built-in functions
sqrt(x)
exp(x)
abs(x)
log(x)
log10(x)
factorial(x)
TRIGONEMETRIC
sin(x)
sind(x)
cos(x)
cosd(x)
tan(x)
tand(x)
cot(x)
cotd(x)
Rounding functions
round(x)
fix(x) - round towards zero
ceil(x)
floor(x)
rem(x,y) – returns the remainder
after x is divided by y
(similar to % function in C)
Display formats
format short : 41.4286
format long:
41.42857142857143
format short e: 4.1429e+001
format long e:
4.142857142857143e+0001
format short g: 41.429
format long g:
41.4285714285714
format bank: 41.43
format compact: eliminates
empty lines
format loose: adds empty lines

5. 5
Plot function
>> x=0:1:5
x =
0 1 2 3 4 5
>> y = sin(10*x) + cos(3*x)
y =
1.0000 -1.5340 1.8731 -1.8992 1.5890 -1.0221
>> plot(x,y)
>> xlabel('x in radians')
>> ylabel('y = sin(10*x) + cos(3*x)')
>>
>> z = zeros(1,6) % alternative way z=0*x
z =
0 0 0 0 0 0
>> plot(x,y, x,z)
>> xlabel('x in radians')
>> ylabel('y = sin(10*x) + cos(3*x)')

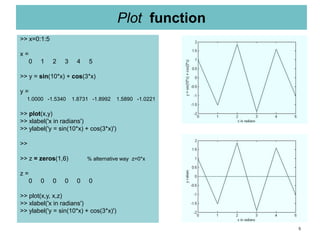
6. 6
Roots of polynomials
>> r = [1, -2, 4]
r =
1 -2 4
>> poly(r)
ans =
1 -3 -6 8
>> p = poly(r)
p =
1 -3 -6 8
>> solve = roots(p)
solve =
4.0000
-2.0000
1.0000
System of equations
>> x=[-1, 5]
x =
-1 5
>> A = [2, 3; -1, 4]
A =
2 3
-1 4
>> b = A*x'
b =
13
21
>> solveX = inv(A)*b
solveX =
-1.0000
5.0000

7. **here Fundamental control structures in MATLAB
Managing Variables
clear – removes all variables from memory clear x y – removes only x and y from memory
who – displays a list of variables in the memory whos – displays a list of variables in the
memory along with their size and class
FOR-Loop sum = 0;
DOFOR i = start, step, final for i = 2:1:25
(Loop Body) sum = sum + A[i];
ENDDO end

8. • Spreadsheet that allows the user to enter and perform calculations on rows
and columns of data.
• When any value on the sheet is changed, entire calculation is updated,
therefore, spreadsheets are ideal for “what if?” sorts of analysis.
• Excel has some built in numerical capabilities including equation solving,
curve fitting and optimization.
• It has several visualization tools, such as graphs and three dimensional
plots.
• It also includes Visual Basic (VBA) as a macro language that can be used
to implement numerical calculations.
check out: http://www.anthony-vba.kefra.com/vba/vbabasic1.htm
EXCEL

10. Special Problem 2