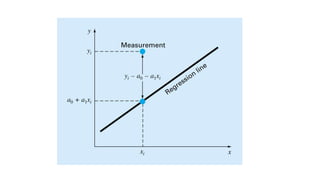
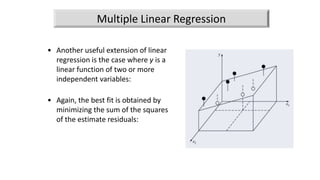
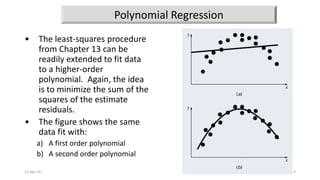
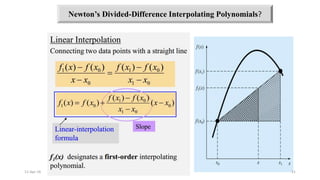
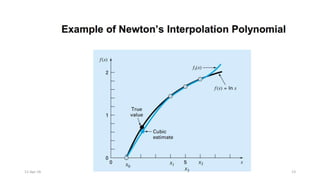
The document presents an exploration of linear regression, multiple linear regression, and polynomial regression, highlighting methods for fitting models to data. It specifies formulas and methodologies for determining parameters such as slope and intercept, and discusses interpolation techniques using Newton's divided difference method. The content outlines the importance of minimizing the sum of squares of error for achieving the best fit in modeling data.

1. Name:Sujit Kumar Saha
Lecturer at Varendra University
Rajshahi
Name: Istiaque Ahmed Shuvo
Id: 141311057
5th batch, 7th Semester
Sec-B
Dept. Of Cse
Varendra University, Rajshahi
Submitted By: Submitted To
11-Apr-16 1

3. TOPICS ARE
 Linear Regression
 Multiple Linear Regression
 Polynomial Regression
 Example of Newton’s Interpolation
Polynomial And example
11-Apr-16 3

4. Fitting a straight line to a set of paired
observations: (x1, y1), (x2, y2),…,(xn, yn).
y = a0+ a1 x + e
a1 - slope
a0 - intercept
e - error, or residual, between the model and
the observations
Linear Regression
11-Apr-16 4

6.  
 
 










2
10
10
1
1
1
0
0
0)(2
0)(2
iiii
ii
iioi
r
ioi
o
r
xaxaxy
xaay
xxaay
a
S
xaay
a
S
 
 





2
10
10
00
iiii
ii
xaxaxy
yaxna
naa
2 equations with 2
unknowns, can be solved
simultaneously
Linear Regression:
Determination of ao and a1
11-Apr-16 6

7.   
  


 221
ii
iiii
xxn
yxyxn
a
xaya 10 
Linear Regression:
Determination of ao and a1
11-Apr-16 7

8. • Another useful extension of linear
regression is the case where y is a
linear function of two or more
independent variables:
• Again, the best fit is obtained by
minimizing the sum of the squares
of the estimate residuals:
Multiple Linear Regression

9. • The least-squares procedure
from Chapter 13 can be
readily extended to fit data
to a higher-order
polynomial. Again, the idea
is to minimize the sum of the
squares of the estimate
residuals.
• The figure shows the same
data fit with:
a) A first order polynomial
b) A second order polynomial
Polynomial Regression
11-Apr-16 9

10. Many times, data is given only at discrete points such as (x0, y0), (x1, y1), ......, (xn−1, yn−1),
(xn, yn). So, how then does one find the value of y at any other value of x ? Well, a
continuous function f (x) may be used to represent the n +1 data values with f (x)
passing through the n +1 points (Figure 1). Then one can find the value of y at any
other value of x . This is called interpolation.
Of course, if x falls outside the range of x for which the data is given, it is no
longer interpolation but instead is called extrapolation.
So what kind of function f (x) should one choose? A polynomial is a common
choice for an interpolating function because polynomials are easy to
(A) evaluate,
(B) differentiate, and
(C) integrate,
relative to other choices such as a trigonometric and exponential series.
Polynomial interpolation involves finding a polynomial of order n that passes
through the n +1 points. One of the methods of interpolation is called Newton’s divided
difference polynomial method. Other methods include the direct method and the
Lagrangian interpolation method. We will discuss Newton’s divided difference
polynomial method in this
What is interpolation?
11-Apr-16 10

11. Newton’s Divided-Difference Interpolating Polynomials?
11-Apr-16 11

12. Example of Newton’s Interpolation Polynomial
11-Apr-16 12

13. 11-Apr-16 13