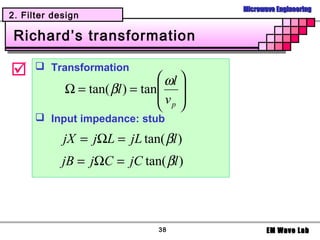
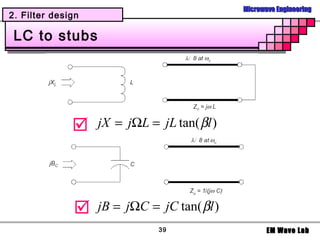
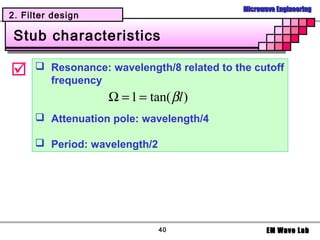
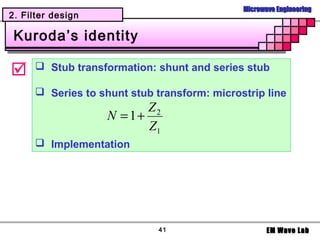
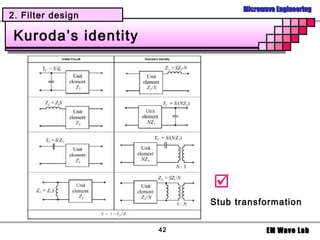
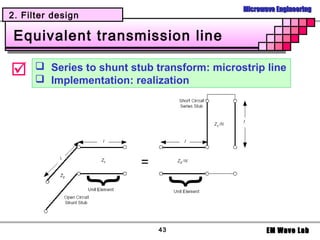
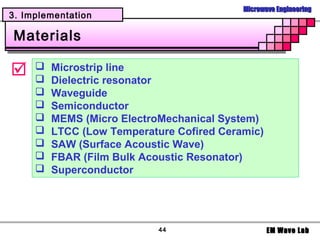
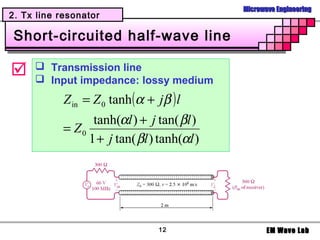
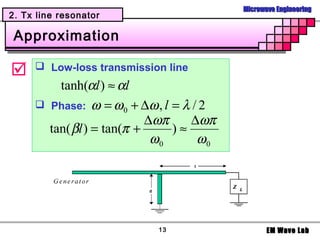
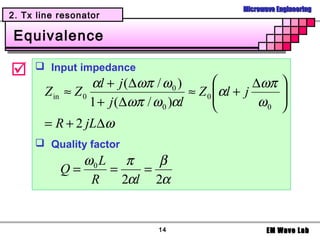
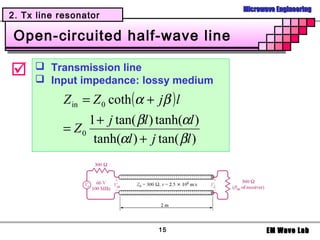
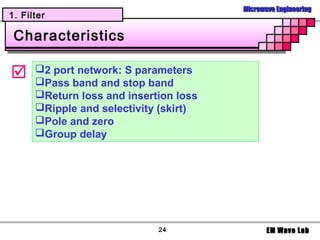
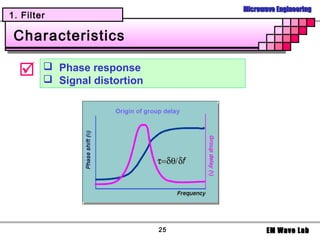
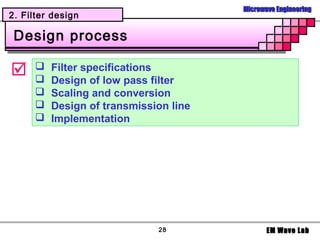
The document discusses microwave filters and resonators. It covers: 1. Different types of resonators used in filters including LC resonators using inductors and capacitors, transmission line resonators using short or open circuited transmission lines, and cavity resonators using rectangular or circular waveguides. 2. Properties of filters like passband, stopband, insertion loss, and group delay. 3. Design of microwave filters including the insertion loss method, filter responses for low pass filters, impedance and frequency scaling, and applying the techniques to different filter types like low pass, high pass, band pass and band stop filters.

1. Microwave
Filter
Microwave Engineering
CHO, Yong Heui

2. Microwave Engineering
Circuit Resonator
2 EM Wave Lab

3. Microwave Engineering
1. LC resonator
Applications
 

Filter
Oscillator
 Frequency meter
 Tuned amplifier
3 EM Wave Lab

4. Microwave Engineering
1. LC resonator
LC resonator: ideal resonator
  Input impedance
j
Z in = jωL −
ωC
 Input power
1 * 1 2 1 2 j 
Pin = VI = Z in I = I  jωL − 
2 2 2  ωC 
 Resonant frequency: Wm = We
1
ω=
LC
4 EM Wave Lab

5. Microwave Engineering
1. LC resonator
Series resonator
  R, L, C
 Input impedance
j
Z in = R + jωL −
ωC
 Input power
1 * 1 2 1 2 j 
Pin = VI = Z in I = I  R + jωL − 
2 2 2  ωC 
 Resonant frequency
1
ω=
LC
5 EM Wave Lab

6. Microwave Engineering
1. LC resonator
Quality factor
  Definition
Average energe stored
Q =ω
Energy loss/second
 3 dB bandwidth
f0
Q=
BW
 Q in terms of R, L, C
2Wm ω 0 L 1
Q = ω0 = =
Pl R ω 0 RC
6 EM Wave Lab

7. Microwave Engineering
1. LC resonator
Perturbation
  Input impedance
 ω 2 − ω0 
2
Z in = R + jωL
 ω 2  ≈ R + j 2 L∆ω

 
7 EM Wave Lab

8. Microwave Engineering
1. LC resonator
Parallel resonator
  R, L, C
 Input admittance
1 j
Yin = − + j ωC
R ωL
 Input power
1 * 1 * 2 1 2 1 j 
Pin = VI = Yin V = V  + − j ωC 
2 2 2  R ωL 
 Resonant frequency
1
ω=
LC
8 EM Wave Lab

9. Microwave Engineering
1. LC resonator
Quality factor
  Q in terms of R, L, C
2Wm R
Q = ω0 = = ω 0 RC
Pl ω0 L
9 EM Wave Lab

10. Microwave Engineering
1. LC resonator
Perturbation
  Input admittance
1  ω 2 − ω0  1
2
Yin = + jωC 
 ω 2  ≈ R + j 2C∆ω

R  
10 EM Wave Lab

11. Microwave Engineering
1. LC resonator
Loaded Q
  Unloaded Q: resonant circuit itself
 Loaded Q: External load resistor
1 1 1
= +
QL Qe Q
11 EM Wave Lab

12. Microwave Engineering
2. Tx line resonator
Short-circuited half-wave line
  Transmission line
 Input impedance: lossy medium
Z in = Z 0 tanh (α + jβ ) l
tanh(αl ) + j tan( βl )
= Z0
1 + j tan( βl ) tanh(αl )
12 EM Wave Lab

13. Microwave Engineering
2. Tx line resonator
Approximation
  Low-loss transmission line
tanh(αl ) ≈ αl
 Phase: ω = ω 0 + ∆ω , l = λ / 2
∆ωπ ∆ωπ
tan( βl ) = tan(π + )≈
ω0 ω0
13 EM Wave Lab

14. Microwave Engineering
2. Tx line resonator
Equivalence
  Input impedance
αl + j (∆ωπ / ω 0 )  ∆ωπ 
Z in ≈ Z 0 ≈ Z 0 αl + j
 

1 + j (∆ωπ / ω 0 )αl  ω0 
= R + 2 jL∆ω
 Quality factor
ω0 L π β
Q= = =
R 2αl 2α
14 EM Wave Lab

15. Microwave Engineering
2. Tx line resonator
Open-circuited half-wave line
  Transmission line
 Input impedance: lossy medium
Z in = Z 0 coth (α + jβ ) l
1 + j tan( βl ) tanh(αl )
= Z0
tanh(αl ) + j tan( βl )
15 EM Wave Lab

16. Microwave Engineering
2. Tx line resonator
Approximation
  Low-loss transmission line
tanh(αl ) ≈ αl
 Phase: ω = ω 0 + ∆ω , l = λ / 2
∆ωπ ∆ωπ
tan( βl ) = tan(π + )≈
ω0 ω0
16 EM Wave Lab

17. Microwave Engineering
2. Tx line resonator
Equivalence
  Input impedance
1 + j (∆ωπ / ω 0 )αl Z0
Z in ≈ Z 0 ≈
αl + j (∆ωπ / ω 0 ) αl + j (∆ωπ / ω 0 )
1
=
1 / R + 2 jC∆ω
 Quality factor
π β
Q = ω 0 RC = =
2αl 2α
17 EM Wave Lab

18. Microwave Engineering
3. Waveguide cavity
Rectangular waveguide
  Metallic wall
 Propagation constant
2 2
 mπ   nπ 
β mn = k −2
 − 
 a   b 
 Resonant condition
β mn d = lπ
18 EM Wave Lab

19. Microwave Engineering
3. Waveguide cavity
Resonant wavenumber
  Resonant wavenumber
2 2 2
 mπ   n π   l π 
k mnl =   +  + 
 a   b  d 
 TE101 mode and TM110 mode
 Q of cavity
2We
Q = ω0
Pl
19 EM Wave Lab

20. Microwave Engineering
3. Waveguide cavity
Circular waveguide
  Metallic wall
 Propagation constant
 Resonant condition
β mn d = lπ
 TE111 mode and TM110 mode
20 EM Wave Lab

21. Microwave Engineering
4. Dielectric cavity
Dielectric material
 

High Q
Fringing field
 High permittivity: magnetic wall
 Mechanical tuning
 TE01δ mode
 Notation
δ = 2 L / λg < 1
21 EM Wave Lab

22. Microwave Engineering
5. Mirror
Fabry-Perot resonator
 

Two mirrors
High Q
 Laser
 Millimeter and optical applications
22 EM Wave Lab

23. Microwave Engineering
Microwave Filter
23 EM Wave Lab

24. Microwave Engineering
1. Filter
Characteristics
 2 port network: S parameters
Pass band and stop band
Return loss and insertion loss
Ripple and selectivity (skirt)
Pole and zero
Group delay
24 EM Wave Lab

25. Microwave Engineering
1. Filter
Characteristics
  Phase response
 Signal distortion
25 EM Wave Lab

26. Microwave Engineering
1. Filter
Classification
 

LPF (Low Pass Filter)
HPF (High Pass Filter)
 BPF (Band Pass Filter)
 BSF (Band Stop Filter): notch filter
26 EM Wave Lab

27. Microwave Engineering
1. Filter
Filter response
 

Maximally flat (Butterworth) filter
Chebyshev filter
 Elliptic function filter
 Bessel function filter
27 EM Wave Lab

28. Microwave Engineering
2. Filter design
Design process
 

Filter specifications
Design of low pass filter
 Scaling and conversion
 Design of transmission line
 Implementation
28 EM Wave Lab

29. Microwave Engineering
2. Filter design
Insertion loss method
  Precise design method
 Power loss ratio: transducer gain
Power available from source 1
PLR = = 2
Power delivered to load 1 − Γ(ω )
 Reflection coefficient
2 M (ω 2 )
Γ(ω ) =
M (ω 2 ) + N (ω 2 )
 Results: M (ω 2 )
PLR = 1 +
N (ω 2 )
29 EM Wave Lab

30. Microwave Engineering
2. Filter design
Filter responses: LPF
  Maximally flat response
2N
ω 
PLR = 1 + k  
2
ω 
 c
 Equal ripple response
ω 
PLR = 1 + k T  
2
ω 
2
N
 c
 Chebyshev polynomial
TN (cosθ ) = cos(nθ )
30 EM Wave Lab

31. Microwave Engineering
2. Filter design
Example
  Design 2-poles low pass filter in terms of the
insertion loss method where ω c = 1, Z S = 1
PLR = 1 + ω 4
Z L (1 − jωZ L C )
Z in = jωL +
1 + (ωZ L C ) 2
31 EM Wave Lab

32. Microwave Engineering
2. Filter design
Impedance scaling
Z L (1 − jωZ L C )
 L′ = Z 0 L Z in = jωL +
1 + (ωZ L C ) 2
C
C′ = Example
Z0 ω0 L
Q=
′
Zs = Z0 R
′
Z L = Z0Z L 1
ω0 =
LC
Series RLC resonator
32 EM Wave Lab

33. Microwave Engineering
2. Filter design
Frequency scaling for LPF
  Basic equation
ω 
PLR (ω ) = PLR  
′ ω 
 c
ω L
jX = j L = j ωL ′  L′ =
ωc ωc
ω C
jB = j C = jωC ′ C′ =
ωc ωc
33 EM Wave Lab

34. Microwave Engineering
2. Filter design
Frequency scaling for HPF
  Basic equation
 ωc 
′
PLR (ω ) = PLR  − 
 ω 
ωc 1 1
jX = − j L=  L′ =
ω j ωC ′ ω cC
ωc 1 1
jB = − j C = C′ =
ω j ωL ′ ωc L
34 EM Wave Lab

35. Microwave Engineering
2. Filter design
Frequency scaling for BPF
  Basic equation: ω 0 = ω1ω 2
  ω ω0  
′  Q
PLR (ω ) = PLR   −  , Q = ω 0
  ω0 ω  
 ω 2 − ω1
 ω ω0  1
 jX = jQ
 ω − ω  L = jωL1′ − jωC ′

 0  1
 ω ω0  1
jB = jQ
ω − C = jωC2 − ′
 0 ω 
 jωL2′
35 EM Wave Lab

36. Microwave Engineering
2. Filter design
Frequency scaling for BSF
  Basic equation: ω 0 = ω1ω 2
 1 ω ω  
−1
′
PLR (ω ) = PLR   0 −  , Q = ω 0
 Q  ω ω0  
   ω 2 − ω1

−1 −1
j  ω0 ω   1 
 jX =  −  L =  ωL′ − ωC1′ 
j 
Q  ω ω0 
   1 
−1 −1
j  ω0 ω   1 
jB =  −  C= j ′
 ωC ′ − ωL2 
Q  ω ω0 
   2 
36 EM Wave Lab

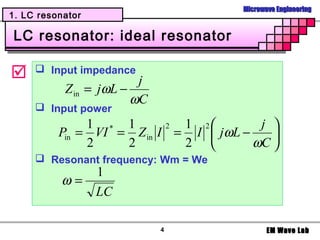
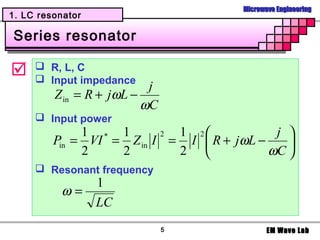
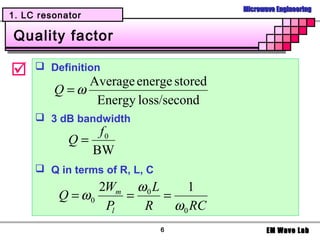
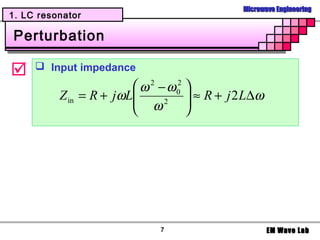
37. Microwave Engineering
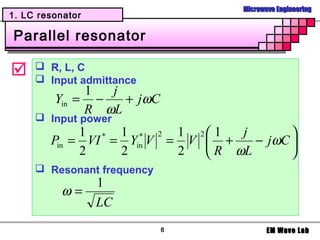
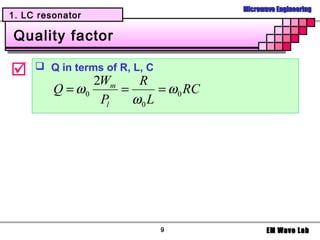
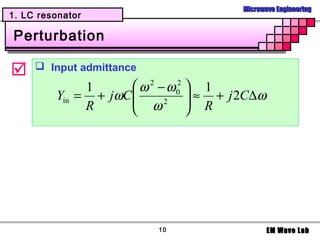
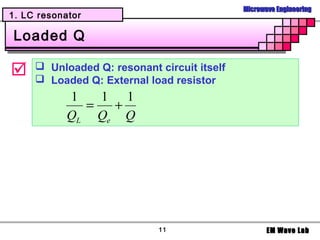
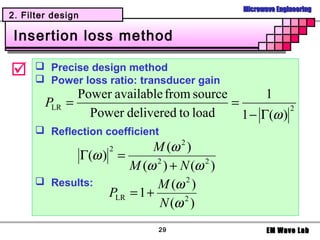
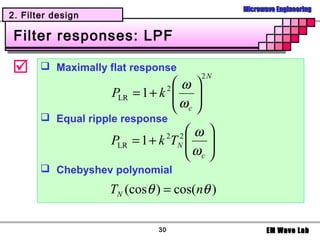
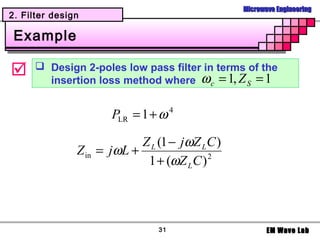
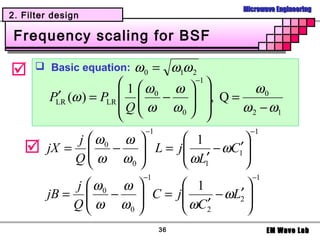
2. Filter design
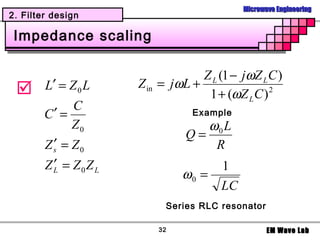
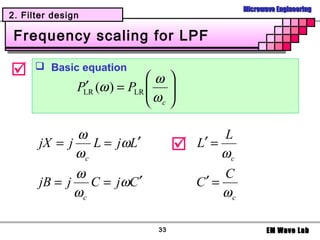
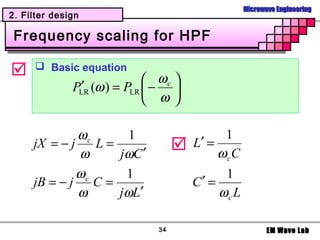
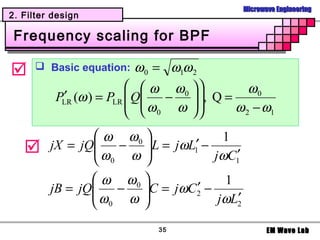
Example
  Design 5-poles low pass filter with a cutoff
frequency of 2 [GHz], impedance = 50 [Ohms],
insertion loss = 15 dB at 3 [GHz]
g1 = 0.618
g 2 = 1.618
g3 = 2
g 4 = 1.618
g 5 = 0.618
Maximally flat response
37 EM Wave Lab

38. Microwave Engineering
2. Filter design
Richard’s transformation
  Transformation
 ωl 
Ω = tan( βl ) = tan 
v 
 p
 Input impedance: stub
jX = jΩL = jL tan( βl )
jB = jΩC = jC tan( βl )
38 EM Wave Lab

39. Microwave Engineering
2. Filter design
LC to stubs
 jX = jΩL = jL tan( βl )
 jB = jΩC = jC tan( βl )
39 EM Wave Lab

40. Microwave Engineering
2. Filter design
Stub characteristics
  Resonance: wavelength/8 related to the cutoff
frequency
Ω = 1 = tan( βl )
 Attenuation pole: wavelength/4
 Period: wavelength/2
40 EM Wave Lab

41. Microwave Engineering
2. Filter design
Kuroda’s identity
  Stub transformation: shunt and series stub
 Series to shunt stub transform: microstrip line
Z2
N = 1+
Z1
 Implementation
41 EM Wave Lab

42. Microwave Engineering
2. Filter design
Kuroda’s identity

Stub transformation
42 EM Wave Lab

43. Microwave Engineering
2. Filter design
Equivalent transmission line
  Series to shunt stub transform: microstrip line
 Implementation: realization
43 EM Wave Lab

44. Microwave Engineering
3. Implementation
Materials
 

Microstrip line
Dielectric resonator
 Waveguide
 Semiconductor
 MEMS (Micro ElectroMechanical System)
 LTCC (Low Temperature Cofired Ceramic)
 SAW (Surface Acoustic Wave)
 FBAR (Film Bulk Acoustic Resonator)
 Superconductor
44 EM Wave Lab