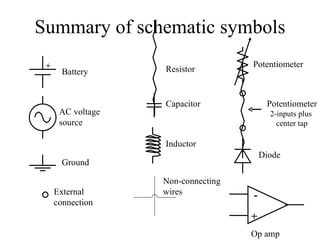
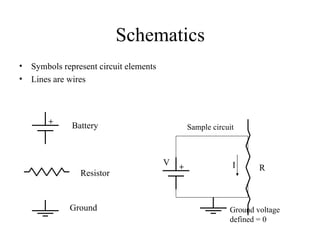
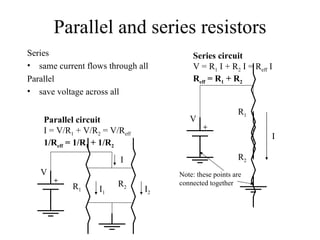
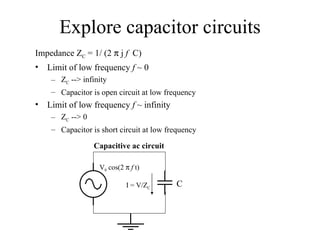
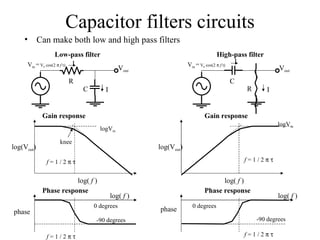
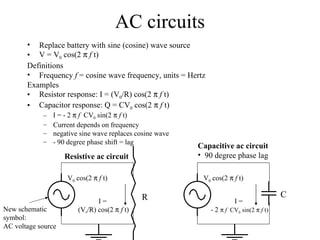
The document provides an overview of basic electronics concepts including: 1) Ohm's law defines the relationship between voltage, current, and resistance in circuits. 2) Schematics use symbols to represent circuit elements and show how they are connected. 3) Resistors in series and parallel follow specific rules to calculate total resistance. 4) Capacitors store charge and their behavior changes with frequency based on impedance.

1. Basic electronics Optical interfaces: Detect and control

2. Ohm’s law Current = voltage / resistance I = V / R V = I x R Definitions Voltage = potential energy / unit charge, units = Volts Current = charge flow rate, units = Amps Resistance = friction, units = Ohms Example Voltage drop when current flows through resistor V 1 - V 2 = I R I R V 1 V 2

3. Schematics Symbols represent circuit elements Lines are wires Battery Resistor Ground V R I Sample circuit Ground voltage defined = 0 + +

4. Parallel and series resistors Series same current flows through all Parallel save voltage across all Series circuit V = R 1 I + R 2 I = R eff I R eff = R 1 + R 2 Parallel circuit I = V/R 1 + V/R 2 = V/R eff 1/R eff = 1/R 1 + 1/R 2 + Note: these points are connected together I V R 1 R 2 + V R 1 R 2 I 1 I 2 I

5. Resistive voltage divider Series resistor circuit Reduce input voltage to desired level Advantages: simple and accurate complex circuit can use single voltage source Disadvantage: dissipates power easy to overload need R load << R 2 New schematic symbol: external connection Resistive divider I = V in /R eff = V out /R 2 V out = V in (R 2 / (R 1 + R 2 ) ) + V in R 1 R 2 I I V out

6. Variable voltage divider Use potentiometer (= variable resistor) Most common: constant output resistance V in R var R out I I V out Variable voltage divider V out = V in (R out / (R var + R out ) ) New schematic symbol: potentiometer +

7. Capacitors Charge = voltage x capacitance Q = C V Definitions Charge = integrated current flow , units = Coloumbs = Amp - seconds I = dQ/dt Capacitance = storage capacity, units = Farads Example Capacitor charging circuit Time constant = RC =  Capacitor charging circuit V = V R + V C = R dQ/dt + Q/C dQ/dt + Q/RC = V/R Q = C V (1 - exp(-t/RC)) V out = V in (1 - exp(-t/RC)) New schematic symbol: capacitor + V R C I V out Q V out t V in  = RC Capacitor charging curve time constant = RC

8. AC circuits Replace battery with sine (cosine) wave source V = V 0 cos(2  f t) Definitions Frequency f = cosine wave frequency, units = Hertz Examples Resistor response: I = (V 0 /R) cos(2  f t) Capacitor response: Q = CV 0 cos(2  f t) I = - 2  f CV 0 sin(2  f t) Current depends on frequency negative sine wave replaces cosine wave - 90 degree phase shift = lag V 0 cos(2  f t) C I = - 2  f CV 0 sin(2  f t) Capacitive ac circuit 90 degree phase lag V 0 cos(2  f t) R I = (V 0 /R) cos(2  f t) Resistive ac circuit New schematic symbol: AC voltage source

9. Simplified notation: ac-circuits V = V 0 cos(2  f t) = V 0 [exp(2  j f t) + c.c.]/2 Drop c.c. part and factor of 1/2 V = V 0 exp(2  j f t) Revisit resistive and capacitive circuits Resistor response: I = (V 0 /R) exp(2  j f t) = V / R = V/ Z R Capacitor response: I = 2  j f CV 0 exp(2  j f t) = (2  j f C) V = V/ Z C Definition: Impedance, Z = effective resistance, units Ohms Capacitor impedance Z C = 1 / (2  j  f C) Resistor impedance Z R = R Impedance makes it look like Ohms law applies to capacitive circuits also Capacitor response I = V / Z C

10. Explore capacitor circuits Impedance Z C = 1/ (2  j  f C) Limit of low frequency f ~ 0 Z C --> infinity Capacitor is open circuit at low frequency Limit of low frequency f ~ infinity Z C --> 0 Capacitor is short circuit at low frequency V 0 cos(2  f t) C I = V/Z C Capacitive ac circuit

11. Revisit capacitor charging circuit Replace C with impedance Z C Charging circuit looks like voltage divider V out = V in (Z C / (Z R + Z C ) ) = V in / (1 + 2  j  f R C ) Low-pass filter Crossover when f = 1 / 2  R C = 1 / 2   ,  is time constant lower frequencies V out ~ V in = pass band higher frequencies V out ~ V in / (2  j  f R C ) = attenuated log(V out ) log(  f ) logV in f = 1 / 2  Low-pass filter response time constant = RC =  Single-pole rolloff 6 dB/octave = 10 dB/decade knee Capacitor charging circuit = Low-pass filter V in = V 0 cos(2  f t) R C I V out I

12. Inductors Voltage = rate of voltage change x inductance V = L dI/dt Definitions Inductance L = resistance to current change, units = Henrys Impedance of inductor: Z L = (2  j  f L) Low frequency = short circuit High frequency = open circuit Inductors rarely used Capacitor charging circuit = Low-pass filter V out log(V out ) log(  f ) logV in f = R / 2  j  L High-pass filter response V in = V 0 cos(2  f t) R L I I New schematic symbol: Inductor

13. Capacitor filters circuits Can make both low and high pass filters 0 degrees 0 degrees Low-pass filter V in = V 0 cos(2  f t) R C I V out I High-pass filter V in = V 0 cos(2  f t) C R I V out I log(V out ) log(  f ) logV in f = 1 / 2  Gain response log(V out ) log(  f ) logV in f = 1 / 2  Gain response knee phase log(  f ) f = 1 / 2  Phase response -90 degrees phase log(  f ) f = 1 / 2  Phase response -90 degrees

14. Summary of schematic symbols + Battery Resistor Ground External connection Capacitor AC voltage source Inductor Non-connecting wires - + Op amp Potentiometer Potentiometer 2-inputs plus center tap Diode

15. Color code Resistor values determined by color Three main bands 1st = 1st digit 2nd = 2nd digit 3rd = # of trailing zeros Examples red, brown, black 2 1 no zeros = 21 Ohms yellow, brown, green 4 1 5 = 4.1 Mohm purple, gray, orange 7 8 3 = 78 kOhms Capacitors can have 3 numbers use like three colors Color black brown red orange yellow green blue violet gray white Number 0 1 2 3 4 5 6 7 8 9