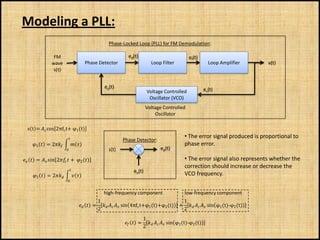
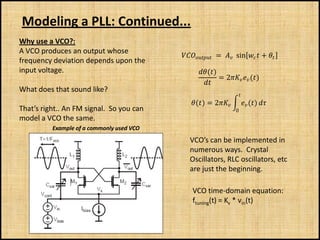
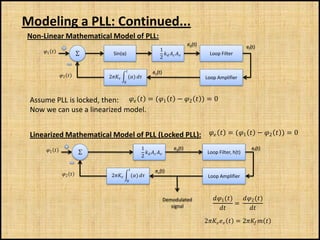
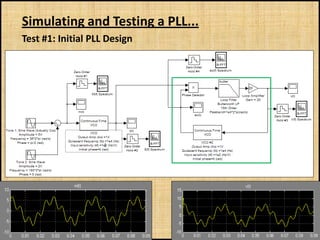
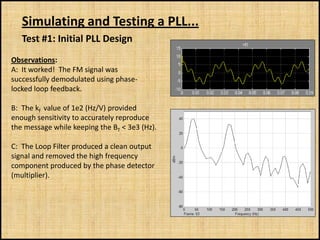
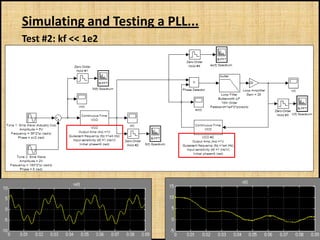
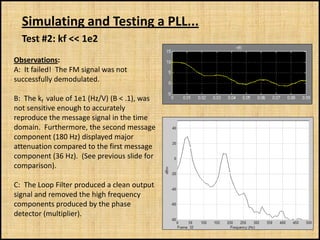
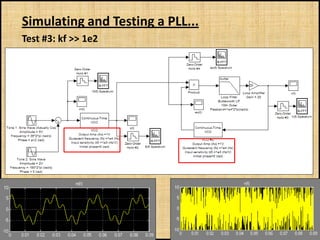
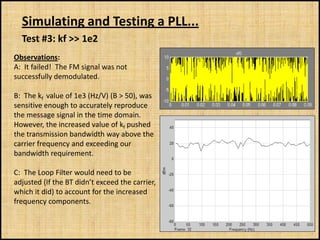
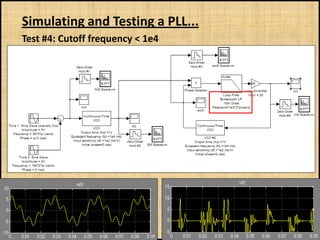
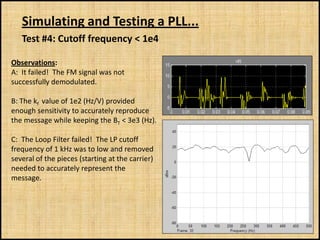
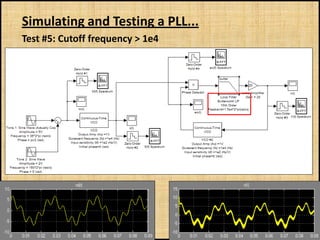
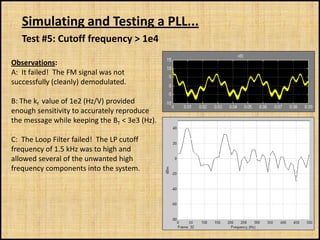
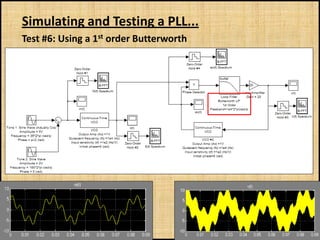
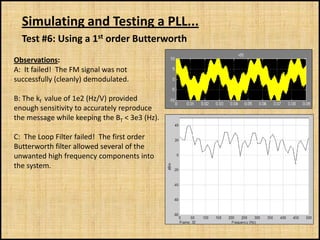
The document discusses phase-locked loops (PLLs), including what they are, how they are modeled and operate, properties of PLLs, and applications. A PLL is a negative feedback system that automatically adjusts the frequency and phase of a control signal to match a reference signal. It consists of a phase detector, loop filter, and voltage-controlled oscillator. The document provides examples of modeling and simulating a PLL using Simulink. It also summarizes tests of a PLL design under different conditions and discusses other applications of PLLs beyond frequency demodulation.

1. Phase-locked loop (PLL)
By:
Loren Schwappach & Crystal Brandy
Prepared for:
Dr. Jing Guo
CTU – EE443 – Communications 1
September 2010

2. Overview
• What is a PLL?
• Modeling a PLL
• Properties of PLLs
• Simulating and Testing a PLL
• Other Applications of PLLs
• Questions
• References

3. What is a phase-locked loop?
• A negative feedback control system whose
operation is closely linked to frequency
modulation (FM).
• Automatically adjusts the frequency, and phase of
a control signal to match a reference signal.
• Commonly used for carrier synchronization and
indirect frequency demodulation.

4. What is a phase-locked loop? Continued...
• A change in the input signal shows up as a change
in phase between the input signal and the VCO
frequency.
• Consists of 3 major components
– Voltage-controlled oscillator (VCO)
• Performs frequency modulation on its own carrier signal
– Phase Detector
• Multiplies an incoming FM wave by the output of the VCO
– Loop filter
• Removes the high-frequency components contained in the
multiplier’s output.

5. Modeling a PLL:
Phase-Locked Loop (PLL) for FM Demodulation:
FM ed(t) ef(t)
wave Phase Detector Loop Filter Loop Amplifier v(t)
s(t)
eo(t)
Voltage Controlled ev(t)
Oscillator (VCO)
Voltage Controlled
Oscillator
s t = cos 2πfc t+ φ1 (t)
• The error signal produced is proportional to
Phase Detector:
1 = 2 phase error.
0 s(t) ed(t)
= 2 + 2 ()
• The error signal also represents whether the
correction should increase or decrease the
eo(t)
2 = 2 VCO frequency.
0
high-frequency component low-frequency component
1 1
= sin 4πfc t+φ1 (t)+φ2 (t) + sin φ1 (t)-φ2 (t)
2 2
1
≈ sin φ1 (t)-φ2 (t)
2

6. Modeling a PLL: Continued...
Why use a VCO?:
A VCO produces an output whose
= sin +
frequency deviation depends upon the
input voltage. ()
= 2 ()
What does that sound like?
() = 2 ()
That’s right.. An FM signal. So you can 0
model a VCO the same.
Example of a commonly used VCO
VCO’s can be implemented in
numerous ways. Crystal
Oscillators, RLC oscillators, etc
are just the beginning.
VCO time-domain equation:
ftuning(t) = Kv * vin(t)

7. Modeling a PLL: Continued...
Non-Linear Mathematical Model of PLL:
ed(t) ef(t)
1 1
∑ Sin(α) Loop Filter
2
ev(t)
2 2 () Loop Amplifier
0
Assume PLL is locked, then: = (1 − 2 ) = 0
Now we can use a linearized model.
Linearized Mathematical Model of PLL (Locked PLL): = (1 − 2 ) = 0
1 1 ed(t) ef(t)
∑ Loop Filter, h(t)
2
ev(t)
2 2 () Loop Amplifier
0
Demodulated 1 () 2 ()
=
signal
2 = 2

8. Properties of phase-locked loops:
• Step response: ability to phase/frequency step on its
input.
• Setting Time: amount of time needed to lock-on
after receiving an input.
• Phase Jitter: Short-term frequency instability causing
small, rapid movements in phase. Often referred to
as phase noise.

9. Simulating and Testing a PLL...
Testing a simple PLL Design (Using Simulink):
Suppose we are given a composite sinusoidal wave:
s t = 5 cos 36 × 2πt + 2sin⁡ (180 × 2πt)
And we would like to frequency modulate and demodulate this wave
with a 10kHz carrier, using a Phase-locked loop feed back system for
demodulation. The transmission bandwidth (BT) is not allowed to exceed
3 kHz.
Design Considerations:
∆ = ×
Carrier frequency (fc) = 10e3 (Hz),
BT < 3e3 (Hz) so kf < 132 (Hz/V) {using max values}, ∆
Let kf = 1e2 (Hz/V) then Beta = approx 5.5 (wideband) =
Let LP filter cutoff at approx 1e4 (Hz)
Things to test: = 2 × ∆ + 2 ×
1. Initial Design = 2 × × + 2 ×
2. What happens when kf << 1e2 (smaller bandwidth)
3. What happens when kf >> 1e2 (larger bandwidth) ×
=
4. What happens when LP Filter cutoff is < 1e4 (Hz)
5. What happens when LP Filter cutoff is > 1e4 (Hz)
6. What happens when we use a 1st order Butterworth.

10. Simulating and Testing a PLL...
Test #1: Initial PLL Design

11. Simulating and Testing a PLL...
Test #1: Initial PLL Design
Observations:
A: It worked! The FM signal was
successfully demodulated using phase-
locked loop feedback.
B: The kf value of 1e2 (Hz/V) provided
enough sensitivity to accurately reproduce
the message while keeping the BT < 3e3 (Hz).
C: The Loop Filter produced a clean output
signal and removed the high frequency
component produced by the phase detector
(multiplier).

12. Simulating and Testing a PLL...
Test #2: kf << 1e2

13. Simulating and Testing a PLL...
Test #2: kf << 1e2
Observations:
A: It failed! The FM signal was not
successfully demodulated.
B: The kf value of 1e1 (Hz/V) (B < .1), was
not sensitive enough to accurately
reproduce the message signal in the time
domain. Furthermore, the second message
component (180 Hz) displayed major
attenuation compared to the first message
component (36 Hz). (See previous slide for
comparison).
C: The Loop Filter produced a clean output
signal and removed the high frequency
components produced by the phase
detector (multiplier).

14. Simulating and Testing a PLL...
Test #3: kf >> 1e2

15. Simulating and Testing a PLL...
Test #3: kf >> 1e2
Observations:
A: It failed! The FM signal was not
successfully demodulated.
B: The kf value of 1e3 (Hz/V) (B > 50), was
sensitive enough to accurately reproduce
the message signal in the time domain.
However, the increased value of kf pushed
the transmission bandwidth way above the
carrier frequency and exceeding our
bandwidth requirement.
C: The Loop Filter would need to be
adjusted (If the BT didn’t exceed the carrier,
which it did) to account for the increased
frequency components.

16. Simulating and Testing a PLL...
Test #4: Cutoff frequency < 1e4

17. Simulating and Testing a PLL...
Test #4: Cutoff frequency < 1e4
Observations:
A: It failed! The FM signal was not
successfully demodulated.
B: The kf value of 1e2 (Hz/V) provided
enough sensitivity to accurately reproduce
the message while keeping the BT < 3e3 (Hz).
C: The Loop Filter failed! The LP cutoff
frequency of 1 kHz was to low and removed
several of the pieces (starting at the carrier)
needed to accurately represent the
message.

18. Simulating and Testing a PLL...
Test #5: Cutoff frequency > 1e4

19. Simulating and Testing a PLL...
Test #5: Cutoff frequency > 1e4
Observations:
A: It failed! The FM signal was not
successfully (cleanly) demodulated.
B: The kf value of 1e2 (Hz/V) provided
enough sensitivity to accurately reproduce
the message while keeping the BT < 3e3 (Hz).
C: The Loop Filter failed! The LP cutoff
frequency of 1.5 kHz was to high and
allowed several of the unwanted high
frequency components into the system.

20. Simulating and Testing a PLL...
Test #6: Using a 1st order Butterworth

21. Simulating and Testing a PLL...
Test #6: Using a 1st order Butterworth
Observations:
A: It failed! The FM signal was not
successfully (cleanly) demodulated.
B: The kf value of 1e2 (Hz/V) provided
enough sensitivity to accurately reproduce
the message while keeping the BT < 3e3 (Hz).
C: The Loop Filter failed! The first order
Butterworth filter allowed several of the
unwanted high frequency components into
the system.

22. Other Applications of PLLs:
• Control Systems
• Frequency Synthesizers
• Jitter reducers
• Digital PLLs
• Clock Generation
• Zero Delay Buffers
• Spread Spectrum Frequency Synthesizers
• Demodulators (QPSK, QAM, FM, FSK, SSB)

23. Conclusion:
A phase locked loop is a negative feedback control system whose operation
can be used to demodulate an FM signal.
The phase-locked loop will automatically adjust it’s frequency and phase
based on an input error voltage and attempt to lock onto a reference signal.
Commonly used for carrier synchronization, indirect frequency demodulation,
clocking, buffering, and jitter removal.
Finally: If you would like to further enhance your understanding of phase-
locked loops, there is an excellent YouTube video by Professor Surendra
Prasad, Department of Electrical Engineering ,IIT Delhi. You can find it at:
http://www.youtube.com/watch?v=NeRdsWYqWFU

24. Questions:

25. References:
Haykin, S., “Analog and Digital Communications 2nd Edition” John
Wiley & Sons, Haboken, NJ, 2007.
Truxal, J. G., Automatic Feedback Control System Synthesis,
McGraw-Hill, New York, 1955.
Gardner, F. M., Phase Lock Techniques, Wiley, New York, Second
Edition, 1967.