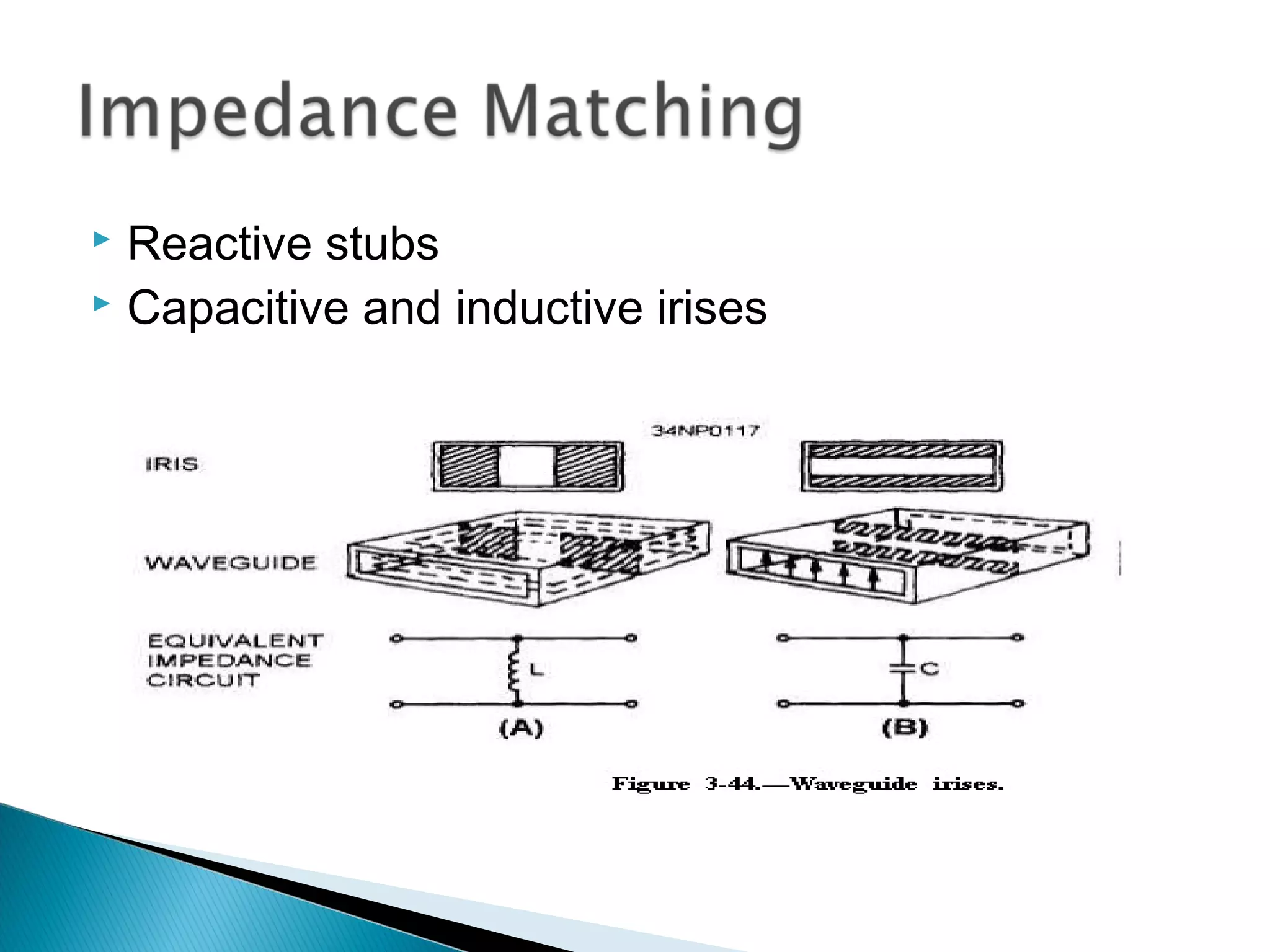
Waveguides are hollow conductive tubes that propagate electromagnetic waves within their interior. They serve as boundaries that confine EM energy through reflection off their walls. Common waveguide types include rectangular, circular, and helical waveguides. Key characteristics of waveguides include their cutoff frequency minimum operating frequency and modes of propagation within the guide.

1. Prepared by: Ronnie Asuncion

2.  Hollow conductive tube
 Usually rectangular in cross section but sometimes
circular or elliptical
 Electromagnetic (EM) waves propagate within its
interior
 Serves as a boundary that confines EM energy
 The walls of it reflect EM energy
 Dielectric within it is usually dehydrated air or inert
gas
 EM energy propagate down in a zigzag pattern

3.  Generally restricted to frequencies above 1 GHz
Rectangular and circular waveguides

4.  Parallel-wire transmission lines and coaxial
cables cannot effectively propagate EM energy
above 20 GHz
 Parallel-wire transmission lines cannot be used
to propagate signals with high powers
 Parallel-wire transmission lines are impractical
for many UHF and microwave applications

5.  Most common form of waveguide
 For an EM wave to exist in the waveguide it
must satisfy Maxwell's equation
Note: A limiting factor of Maxwell’s equation is
that a transverse electromagnetic (TEM) wave
cannot have a tangential component of the
electric field at the walls of the waveguide
 EM wave cannot travel straight down a
waveguide without reflecting off the sides

6.  The TEM wave must propagate in a zigzag
manner to successfully propagate through the
waveguide with the electric field maximum at the
center of the guide and zero at the surface of
the walls

7.  In parallel-wire transmission lines, wave velocity is
independent of frequency, and for air or vacuum
dielectrics, the velocity is equal to the velocity in free
space
 In waveguides the velocity varies with frequency
 Group and phase velocities have the same value in
free space and in parallel-wire transmission lines
 The velocities are not the same in waveguide if
measured at the same frequency
 At some frequencies they will be nearly equal and at
other frequencies they can be considerably different

8.  The phase velocity is always equal; to greater
than the group velocity
 The product of the two velocities is equal to the
square of the free space propagation speed
Vg Vph = c^2
where:
Vph = phase velocity (meters/second)
Vg = group velocity (meters/second)
c = free space propagation speed
= 300,000,000 (meters/second)

9.  The velocity of group waves
 The velocity at which information signals of any
kind are propagated
 The velocity at which energy is propagated
 Can be measured by determining the time it
takes for a pulse to propagate a given length of
waveguide

10.  The apparent velocity of a particular phase of the wave
 The velocity with which a wave changes phase in a
direction parallel to a conducting surface, such as the walls
of a waveguide
 Determined by increasing the wavelength of a particular
frequency wave, then substituting it into the formula:
Vph = f λ
where:
Vph = phase velocity (meters/second)
f = frequency (hertz)
λ = wavelength (meters/second)

11.  may exceed the velocity of light
 Phase velocity in waveguide is greater than its
velocity in free space
 Wavelength for a given frequency will be greater
in the waveguide than in free space

12.  Free space wavelength, guide wavelength,
phase velocity and free space velocity of
electromagnetic wave relationship:
λg = λo (Vph / c)
where:
λg = guide wavelength (meter/cycle)
λo = guide wavelength (meter/cycle)
Vph = phase velocity (meters/second)
c = free space velocity (meter)

13. Cutoff Frequency - minimum frequency of operation
- an absolute limiting frequency
Cutoff Wavelength - maximum wavelength that can
be propagated down the waveguide
-smallest free-space wavelength
that is just unable to propagate in
the waveguide

14.  The relationship between the guide wavelength
at a particular frequency is:
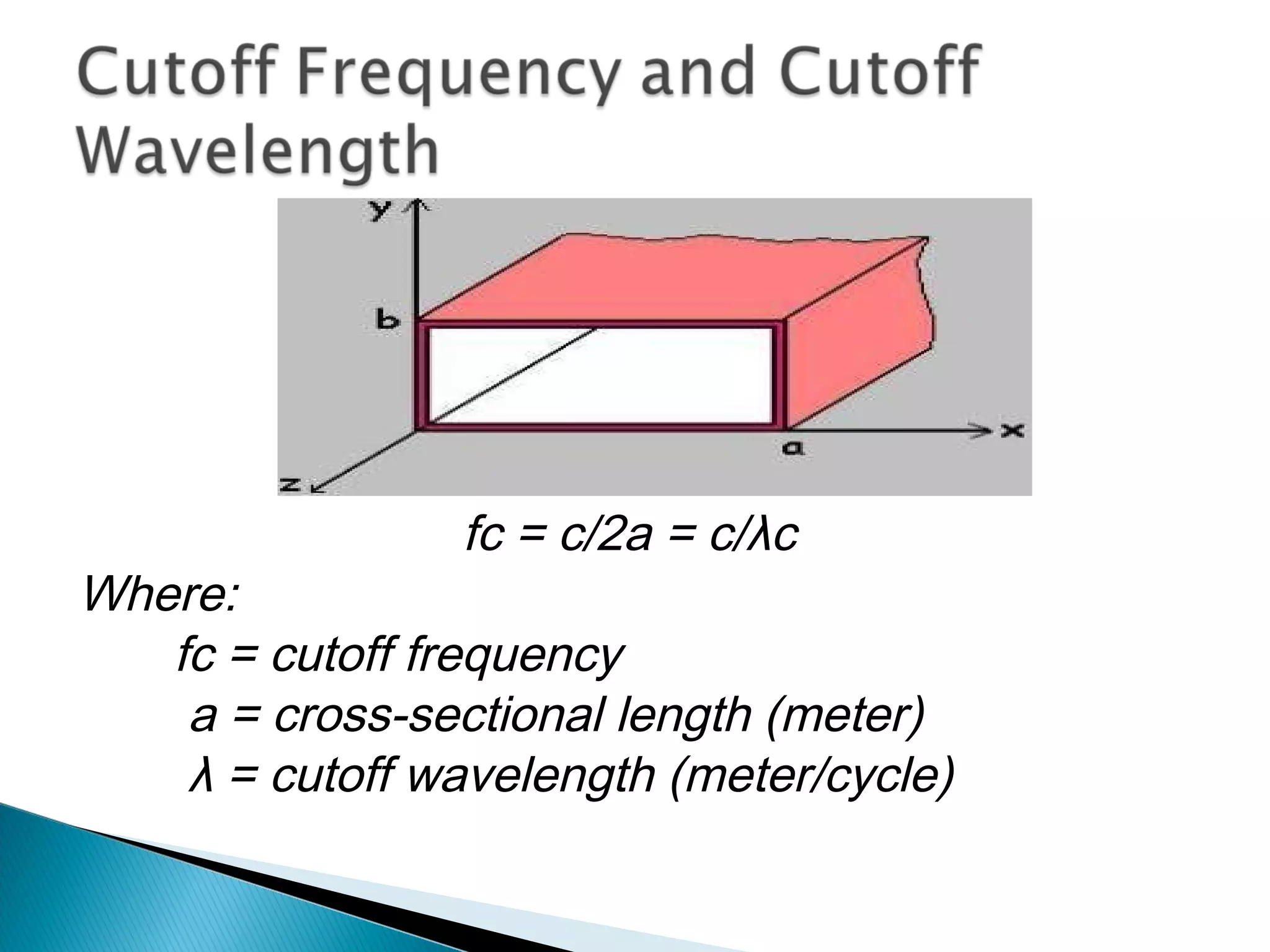
λg = (c) / [(f^2)-(fc^2)]^(1/2)
where:
λg = guide wavelength (meter/cycle)
fc = cutoff frequency (hertz)
f = frequency of operation (hertz)
 Determined by the cross-sectional dimension of the
waveguide

15. fc = c/2a = c/λc
Where:
fc = cutoff frequency
a = cross-sectional length (meter)
λ = cutoff wavelength (meter/cycle)

16.  Electromagnetic waves travel down a waveguide in
different configurations called propagation modes
 There are two propagation modes:
- TEm,n for transverse-electric waves
- TMm,n for transverse-magnetic waves
 TE1,0 is the dominant mode for rectangular waveguide
 At frequencies above the fc, higer order TE modes are
possible

17.  It is undesirable to operate a waveguide at
frequency at which higher modes can propagate
 Next higher mode possible occurs when the free
space λ is equal to a
 A rectangular waveguide is normally operated within the
frequency range between fc and 2fc

18. Zo = 377/{1-(fc/f)^2} = 377(λg/ λo)
Where:
Zo - characteristic impedance (ohms)
fc - cutoff frequency
f - frequency of operation

19.  Reactive stubs
 Capacitive and inductive irises

20.  Used in radar and microwave applications
 The behavior of electromagnetic waves in
circular waveguides is the same as it is
rectangular waveguides
 Are easier to manufacture than rectangular
waveguides
 Disadvantage is that the plane of polarization
may rotate while the signal is propagating down
it.

21.  Cutoff wavelength, λo
λo = 2πr/kr
where:
λo = Cutoff wavelength (meters/cycle)
r = internal radius of the waveguide
kr = solution of Bessel function equation
 TE1,1 is the dominant mode for circular waveguides
the cutoff wavelength for this mode is:
λo = 1.7d
d = waveguide diameter

22.  Consist of spiral wound ribbons of brass or
copper
 Short pieces of the guide are used in microwave
systems when several transmitters and
receivers are interconnected to a complex
combining or separating unit
 Used extensively in microwave test equipment