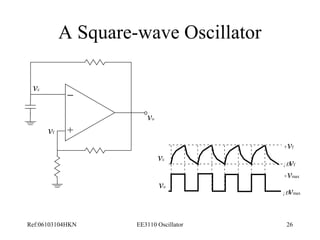
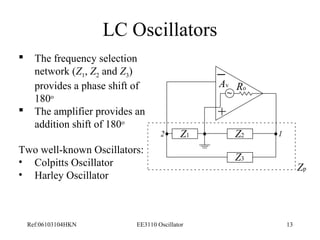
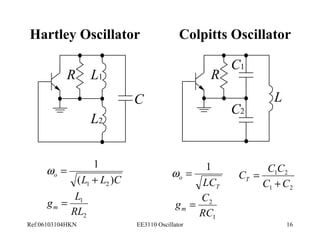
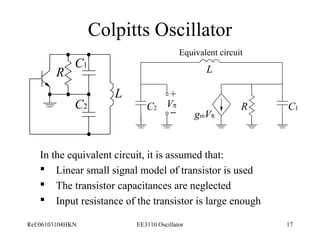
This document discusses oscillators and their various types. It begins with an introduction to oscillators and their characteristics. It then describes different types of linear oscillators, including Wien bridge, RC phase-shift, and LC oscillators. It also discusses oscillator stability and applications such as generating signals for receivers, transmitters, and digital clocks. Specific oscillator circuits like Colpitts and Hartley are analyzed.

1. Lecture 3 Oscillator
• Introduction of Oscillator
• Linear Oscillator
– Wien Bridge Oscillator
– RC Phase-Shift Oscillator
– LC Oscillator
• Stability
Ref:06103104HKN EE3110 Oscillator 1

2. Oscillators
Oscillation: an effect that repeatedly and
regularly fluctuates about the mean value
Oscillator: circuit that produces oscillation
Characteristics: wave-shape, frequency,
amplitude, distortion, stability
Ref:06103104HKN EE3110 Oscillator 2

3. Application of Oscillators
• Oscillators are used to generate signals, e.g.
– Used as a local oscillator to transform the RF
signals to IF signals in a receiver;
– Used to generate RF carrier in a transmitter
– Used to generate clocks in digital systems;
– Used as sweep circuits in TV sets and CRO.
Ref:06103104HKN EE3110 Oscillator 3

4. Linear Oscillators
1. Wien Bridge Oscillators
2. RC Phase-Shift Oscillators
3. LC Oscillators
4. Stability
Ref:06103104HKN EE3110 Oscillator 4

5. Integrant of Linear Oscillators
Ve
+ Amplifier (A)
Vs Vo
S
+
Frequency-Selective
Feedback Network (b)
Vf
Positive
Feedback
For sinusoidal input is connected
“Linear” because the output is approximately sinusoidal
A linear oscillator contains:
- a frequency selection feedback network
- an amplifier to maintain the loop gain at unity
Ref:06103104HKN EE3110 Oscillator 5

6. Basic Linear Oscillator
+
Ve A(f)
Vs Vo
S
+
SelectiveNetwork
b(f)
Vf
( ) o s f V = AV = A V +V e and f o V = bV
A
Ab
V
s
Þ o
=
V
-
1
If Vs = 0, the only way that Vo can be nonzero
is that loop gain Ab=1 which implies that
A (Barkhausen Criterion)
b
A
=
b
| | 1
Ð =
0
Ref:06103104HKN EE3110 Oscillator 6

7. Wien Bridge Oscillator
1
C
1
C
Let Frequency Selection Network
= and
1
XC 1
w
1 1 C1 Z = R - jX
2
X=
C 2
w
C
jR X
2 2
2 2
1
2 2
ù
é
Vi Vo
jR X R jX
= - -
( / )
C C
2 2 2 2
2
V
o
Z
C
jR X
2 2
b = -
R - jX R - jX -
jR X
( )( ) C C C
Ref:06103104HKN EE3110 Oscillator 7
2
1 1
C
C R jX
R jX
Z
-
= - úû
êë
-
= +
-
Therefore, the feedback factor,
( ) ( / )
1 1 2 2 2 2
1 2
C C C
i
R jX jR X R jX
Z Z
V
- + - -
+
b = =
1 1 2 2 2 2
R1 C1
C2 R2
Z1
Z2

8. b can be rewritten as:
C
R X
2 2
R X + R X + R X + j R R -
X X
( ) 1 C 2 2 C 1 2 C 2 1 2 C 1 C
2
b =
For Barkhausen Criterion, imaginary part = 0, i.e.,
0 1 2 1 2 - = C C R R X X
or 1 1
C C
w w
1 2
R R C C
1 2 1 2
R R
1 2
1/
Þ =
=
w
Supposing,
R1=R2=R and XC1= XC2=XC,
RX
C
+ -
3 RX j ( R 2 X
2 )
C C
b =
0.34 b
0.32
factor 0.3
0.28
Feedback 0.26
0.24
0.22
0.2
1
0.5
0
Phase
-0.5
-1
f(R=Xc)
Phase=0
Frequency
b=1/3
Ref:06103104HKN EE3110 Oscillator 8

9. Example
Rf
-
+
R
R
C
R1
C
Z1
Z2
Vo
w = 1
By setting RC
, we get
b = 1
Imaginary part = 0 and
3
Due to Barkhausen Criterion,
Loop gain Avb=1
where
Av : Gain of the amplifier
R
A A f
v v b = Þ = = +
R
1
1 3 1
RTherefore, f 2
Wien Bridge Oscillator
=
R
1
Ref:06103104HKN EE3110 Oscillator 9

10. RC Phase-Shift Oscillator
-
+
Rf
R1
C C C
R R R
 Using an inverting amplifier
 The additional 180o phase shift is provided by an RC
phase-shift network
Ref:06103104HKN EE3110 Oscillator 10

11. Applying KVL to the phase-shift network, we have
C C C
V1 Vo
R R R
V = I ( R - jX )
-
I R
C
1 1 2
I R I R jX I R
= - + - -
0 (2 )
C
1 2 3
I R I R jX
= - + -
0 (2 )
2 3
C
I1 I2 I3 Solve for I3, we get
C
R - jX -
R
0
R R jX R
- - -
C
C
R jX R V
1
2 0
C
- -
C
R R jX
R R jX
R
I
- -
- -
-
=
2
0 2
0 0
3
2
I V R
1
( )[(2 )2 2 ] 2 (2 )
Or =
3
R - jX R - jX - R - R R -
jX
C C C Ref:06103104HKN EE3110 Oscillator 11

12. The output voltage,
3
V = I R =
V R
1
o R jX R jX R R R jX
( )[(2 )2 2 ] 2 (2 )
3
- - - - -
C C C
Hence the transfer function of the phase-shift network is given by,
3
R
( 3 5 2 ) ( 3 6 2 )
V
b = o
=
R RX j X R X
V
- + -
1 C C C
For 180o phase shift, the imaginary part = 0, i.e.,
3 2
X R X XC C C
- = =
6 0 or 0 (Rejected)
2C
R
2 1
RC
Þ =
X 6
6
=
w
and,
b = - 1
29
Note: The –ve sign mean the
phase inversion from the
voltage
Ref:06103104HKN EE3110 Oscillator 12

13. LC Oscillators
-
~
Av Ro
+
Z1 Z2
2 1
Z3
Ref:06103104HKN EE3110 Oscillator 13
Zp
 The frequency selection
network (Z1, Z2 and Z3)
provides a phase shift of
180o
 The amplifier provides an
addition shift of 180o
Two well-known Oscillators:
• Colpitts Oscillator
• Harley Oscillator

14. Av Ro
+
~
Z1 Z2
Vf Vo
Z3
Zp
V V Z
f o o V
1
+
Z Z
1 3
= b =
Z = Z Z +
Z p
//( )
2 1 3
( )
Z Z Z
= +
2 1 3
Z + Z +
Z
1 2 3
For the equivalent circuit from the output
A Z
v p
-
R +
Z
o p
V
- or
= o
=
V
i
V
o
p
A V
v i
R +
Z
o p
Z
Ro
Io
-A Zp vVi
+
-
+
Vo
-
Therefore, the amplifier gain is obtained,
A Z Z Z
= = - +
( )
2 1 3
v
R Z + Z + Z + Z Z +
Z
( ) ( )
1 2 3 2 1 3
A V
o
V
o
i
Ref:06103104HKN EE3110 Oscillator 14

15. The loop gain,
A A Z Z
1 2
v
b = -
R Z + Z + Z + Z Z +
Z
( ) ( ) 1 2 3 2 1 3
o
If the impedance are all pure reactances, i.e.,
1 1 2 2 3 3 Z = jX , Z = jX and Z = jX
The loop gain becomes,
A A X X
1 2
v
jR X + X + X - X X +
X
( ) ( ) 1 2 3 2 1 3
o
b =
The imaginary part = 0 only when X1+ X2+ X3=0
 It indicates that at least one reactance must be –ve (capacitor)
 X1 and X2 must be of same type and X3 must be of opposite type
A AvX = v
A X
2
1
1
With imaginary part = 0, b = -
X +
X
1 3
X
For Unit Gain & 180o Phase-shift,
A A X v b = Þ =
1 2
1
X
Ref:06103104HKN EE3110 Oscillator 15

16. Hartley Oscillator Colpitts Oscillator
R L1
L2
C
R
C1
C2
L
w = 1
1
w =
L L C = o ( )
o LC
T
g C m =
2
RC
1
C C C T +
1 2
C C
1 2
1 2 +
g L m =
1
RL
2
Ref:06103104HKN EE3110 Oscillator 16

17. Colpitts Oscillator
R
C1
C2
L
Equivalent circuit
+
-
Vp
L
C2 R C1
gmVp
In the equivalent circuit, it is assumed that:
 Linear small signal model of transistor is used
 The transistor capacitances are neglected
 Input resistance of the transistor is large enough
Ref:06103104HKN EE3110 Oscillator 17

18. At node 1,
( ) 1 1 V V i jwL p = +
where,
p i jwC V 1 2 =
2
L
node 1
I1
I2 I3
V1
C2 R C1
Þ V = V (1 -
w LC ) 1 p 2
Apply KCL at node 1, we have
j C V g V V m w w p p
2 + + + j CV =
Vp
0 1 1
1
R
+
-
gmVp
(1 ) 1 0 2 1
+ + - 2
æ + j C
ö çè
j C V g V V LC m w w w p p p
2 R
÷ø
= For Oscillator Vp must not be zero, therefore it enforces,
ö
1 [ ( ) ] 0
gm w w w
= - + + ÷ ÷ø
LC
+ - j C C LC C
1 2
3
1 2
2
2
æ
ç çè
R
R
I4
Ref:06103104HKN EE3110 Oscillator 18

19. ö
1 [ ( ) ] 0
gm w w w
= - + + ÷ ÷ø
LC
+ - j C C LC C
1 2
2
2
æ
ç çè
R
R
Imaginary part = 0, we have
1 2
3
w = 1
o LC
T
Real part = 0, yields
g C m =
2
RC
1
C C C T +
1 2
C C
1 2
=
Ref:06103104HKN EE3110 Oscillator 19

20. Frequency Stability
• The frequency stability of an oscillator is
defined as
o
ppm/ C
w
1 ×æ
ö çè
÷ø
w =
T
d
w w
o o d
• Use high stability capacitors, e.g. silver
mica, polystyrene, or teflon capacitors and
low temperature coefficient inductors for
high stable oscillators.
Ref:06103104HKN EE3110 Oscillator 20

21. Amplitude Stability
• In order to start the oscillation, the loop
gain is usually slightly greater than unity.
• LC oscillators in general do not require
amplitude stabilization circuits because of
the selectivity of the LC circuits.
• In RC oscillators, some non-linear devices,
e.g. NTC/PTC resistors, FET or zener
diodes can be used to stabilized the
amplitude
Ref:06103104HKN EE3110 Oscillator 21

22. Wien-bridge oscillator with bulb stabilization
Vrms
irms
Operating
point
+
-
R
R
C
C
R2
Blub
Ref:06103104HKN EE3110 Oscillator 22

23. Wien-bridge oscillator with diode
stabilization
Rf
-
+
R
R
C
R1
C
Vo
Ref:06103104HKN EE3110 Oscillator 23

24. Twin-T Oscillator
-
+
low pass filter
high pass filter
Filter output
low pass region high pass region
fr f
Ref:06103104HKN EE3110 Oscillator 24

25. Bistable Circuit
+
-
vo
v1
v+
Vth
+Vcc
-Vcc
vo
v1
-Vth
vo
+Vcc
-Vcc
v1
Vth
+Vcc
-Vth
-Vcc
vo
v1
Ref:06103104HKN EE3110 Oscillator 25

26. A Square-wave Oscillator
-
+
vo
vc
vf
vc
vo
+vf
¡Ðvf
+vmax
¡Ðvmax
Ref:06103104HKN EE3110 Oscillator 26