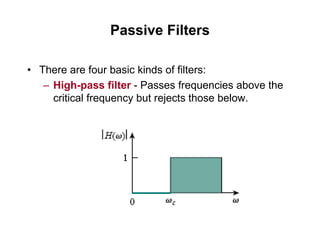
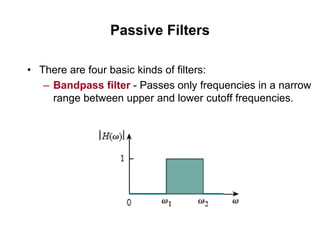
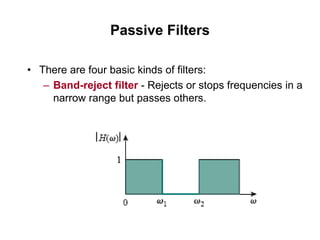
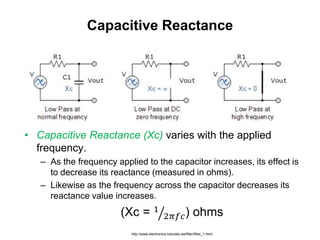
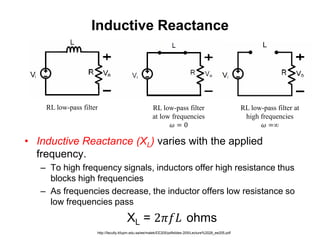
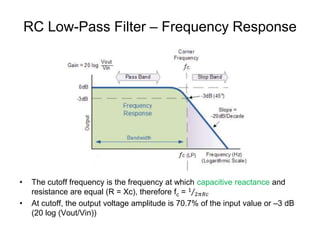
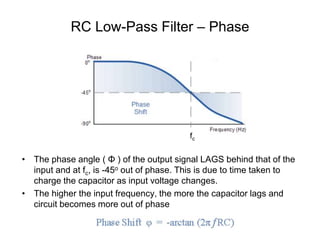
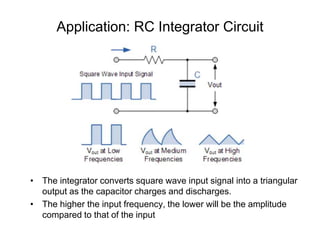
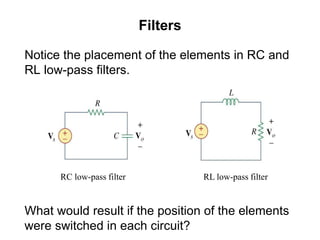
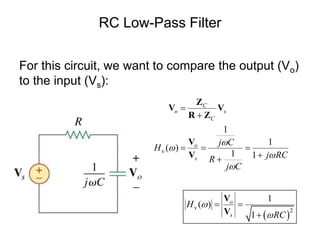
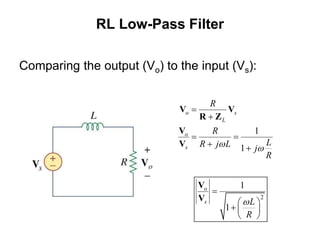
This document discusses passive filters, which are composed only of passive components like resistors, capacitors, and inductors. There are four basic types of passive filters: low-pass filters, which pass frequencies below a cutoff frequency; high-pass filters, which pass frequencies above a cutoff frequency; bandpass filters, which pass a narrow range of frequencies between upper and lower cutoff frequencies; and band-reject filters, which reject a narrow range of frequencies but pass others. The document provides examples of RC and RL low-pass and high-pass filter circuits and discusses how their frequency response depends on the component values.

1. Passive Filters

2. 90.7
WSDL
Ocean City
90.3
WHID
Salisbury
Frequency
(MHz)
90.5
WKHS
Worton
91.3
WMLU
Farmville
90.9
WETA
Washington
91.1
WHFC
Bel Air
91.5
WBJC
Baltimore
Tuning a Radio
• Consider tuning in an FM radio station.
• What allows your radio to isolate one station from all of
the adjacent stations?

3. Filters
• A filter is a frequency-selective circuit.
• Filters are designed to pass some frequencies and reject
others.
Frequency
(MHz)
90.9
WETA
Washington

4. Active and Passive Filters
• Filter circuits depend on the fact that the impedance of
capacitors and inductors is a function of frequency
• There are numerous ways to construct filters, but there
are two broad categories of filters:
– Passive filters are composed of only passive
components (resistors, capacitors, inductors) and do
not provide amplification.
– Active filters typically employ RC networks and
amplifiers (opamps) with feedback and offer a number
of advantages.

5. Passive Filters
• There are four basic kinds of filters:
– Low-pass filter - Passes frequencies below a critical
frequency, called the cutoff frequency, and attenuates
those above.

6. Passive Filters
• There are four basic kinds of filters:
– High-pass filter - Passes frequencies above the
critical frequency but rejects those below.

7. Passive Filters
• There are four basic kinds of filters:
– Bandpass filter - Passes only frequencies in a narrow
range between upper and lower cutoff frequencies.

8. Passive Filters
• There are four basic kinds of filters:
– Band-reject filter - Rejects or stops frequencies in a
narrow range but passes others.

9. Low Pass Filters
RL low-pass filterRC low-pass filter
• RC low pass filter works based on the principle of
capacitive reactance, while RL low pass filter works on
the principle of inductive reactance
http://www.learningaboutelectronics.com/Articles/Low-pass-filter.php

10. Capacitive Reactance
• Capacitive Reactance (Xc) varies with the applied
frequency.
– As the frequency applied to the capacitor increases, its effect is
to decrease its reactance (measured in ohms).
– Likewise as the frequency across the capacitor decreases its
reactance value increases.
(Xc = 1
2𝜋𝑓𝑐) ohms
http://www.electronics-tutorials.ws/filter/filter_1.html

11. Inductive Reactance
• Inductive Reactance (XL) varies with the applied
frequency.
– To high frequency signals, inductors offer high resistance thus
blocks high frequencies
– As frequencies decrease, the inductor offers low resistance so
low frequencies pass
XL = 2𝜋𝑓𝐿 ohms
http://faculty.kfupm.edu.sa/ee/malek/EE205/pdfslides-205/Lecture%2028_ee205.pdf
RL low-pass filter RL low-pass filter
at low frequencies
𝜔 = 0
RL low-pass filter at
high frequencies
𝜔 =∞

12. RC Low-Pass Filter – Frequency Response
• The cutoff frequency is the frequency at which capacitive reactance and
resistance are equal (R = Xc), therefore fc = 1
2𝜋𝑅𝑐
• At cutoff, the output voltage amplitude is 70.7% of the input value or –3 dB
(20 log (Vout/Vin))

13. RC Low-Pass Filter – Phase
• The phase angle ( Φ ) of the output signal LAGS behind that of the
input and at fc, is -45o out of phase. This is due to time taken to
charge the capacitor as input voltage changes.
• The higher the input frequency, the more the capacitor lags and
circuit becomes more out of phase
fc

14. Application: RC Integrator Circuit
• The integrator converts square wave input signal into a triangular
output as the capacitor charges and discharges.
• The higher the input frequency, the lower will be the amplitude
compared to that of the input

15. Filters
Notice the placement of the elements in RC and
RL low-pass filters.
What would result if the position of the elements
were switched in each circuit?
RL low-pass filterRC low-pass filter

16. RC and RL High-Pass Filter Circuits
Switching elements results in a High-Pass Filter.
co co
1
or [Hz]
2 2
R
f f
RC L 
 
f (Hz)fco
actual
passbandreject-band
“ideal”
cutoff frequency
o
s
V
V
0 dB
–3 dB

17. Impedance vs. Frequency
Calculate the impedance of a resistor, a capacitor
and an inductor at the following frequencies.
1
L CZ j L Z j
C
 
     
 
f 100 Hz 1000 Hz 10,000 Hz
R 100 W 100 W 100 W
ZL j10 W j100 W j1000 W
ZC -j1000 W -j100 W -j10 W

18. RC Low-Pass Filter
For this circuit, we want to compare the output (Vo)
to the input (Vs):
 
v
v 2
1
1
( )
1 1
1
( )
1
C
o s
C
o
s
o
s
j C
H
j RCR
j C
H
RC








  

 

Z
V V
R Z
V
V
V
V

19. Example
What is the cutoff frequency for this filter?
Given:
8.2
0.0033
R k
C F
 W
 
co
coor [Hz]
2
RC
f
RC






co 5.88 kHzf 

20. RL Low-Pass Filter
Comparing the output (Vo) to the input (Vs):
2
1
1
1
1
o s
L
o
s
o
s
R
R
LR j L j
R
L
R
 



 
 

 
  
 
V V
R Z
V
V
V
V

21. EXAMPLE – RL Low Pass Filter
Design a series RL low-pass filter to filter out any noise above 10 Hz.
R and L cannot be specified independently to generate a value for fco = 10 Hz
or co = 2fco. Therefore, let us choose L=100 mH. Then,
3
(2 )(10)(100 10 ) 6.28coR L  
    W
 
2 2 22
20
( )
400
R
L
o s s
R
L
V V V


 
 

f(Hz) |Vs| |Vo|
1 1.0 0.995
10 1.0 0.707
60 1.0 0.164
co co2
1
which implies: or [Hz]
2
1
o
s
R R
f
L LL
R


  
 
  
 
V
V

22. Example: Microphone circuit

23. Example
What resistor value R will produce a cutoff frequency of 3.4 kHz
with a 0.047 mF capacitor? Is this a high-pass or low-pass filter?
co
co
1
[Hz]
2
1
R=
2
f
RC
C f




1004R  W
This is a High-Pass Filter