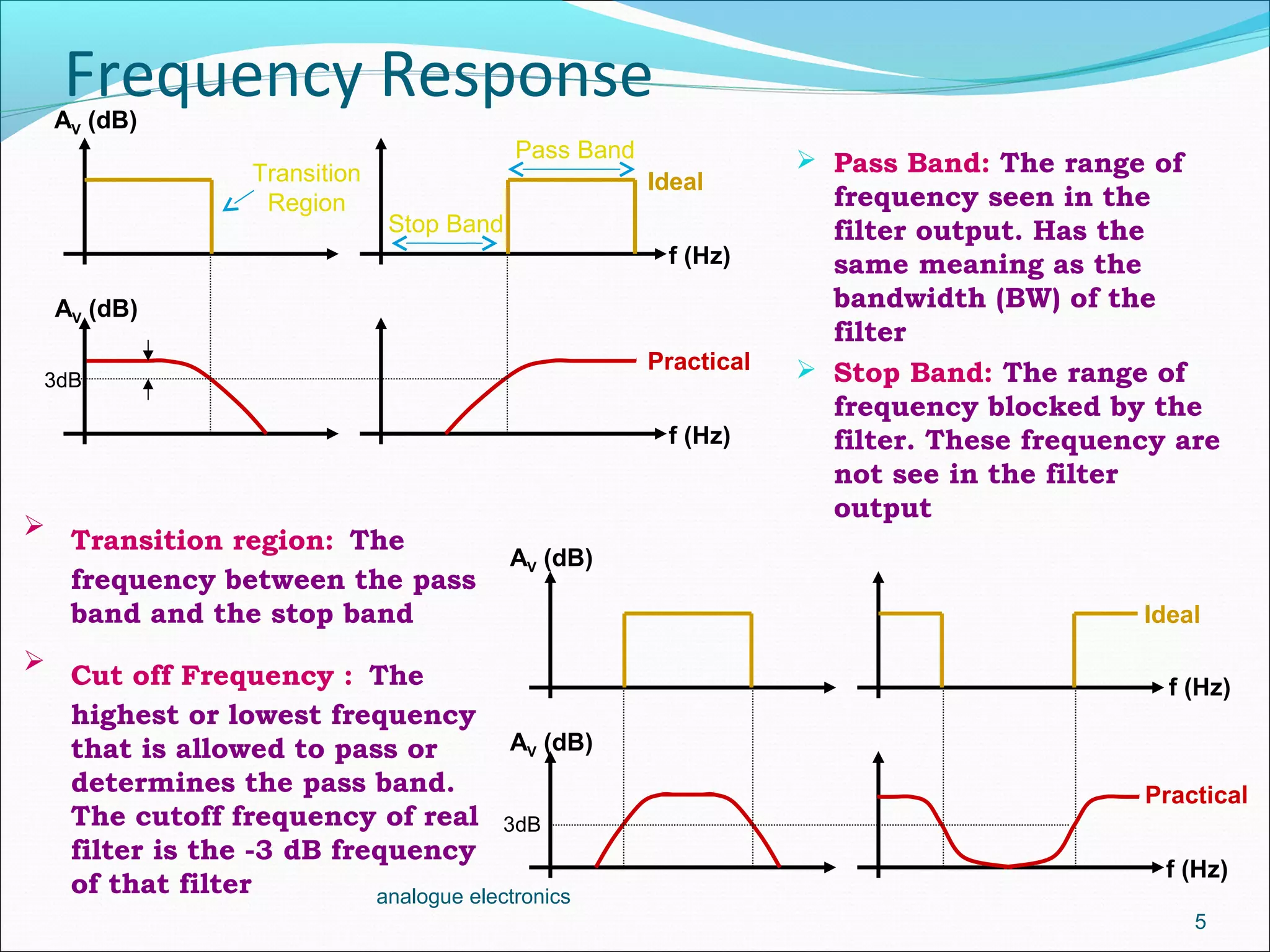
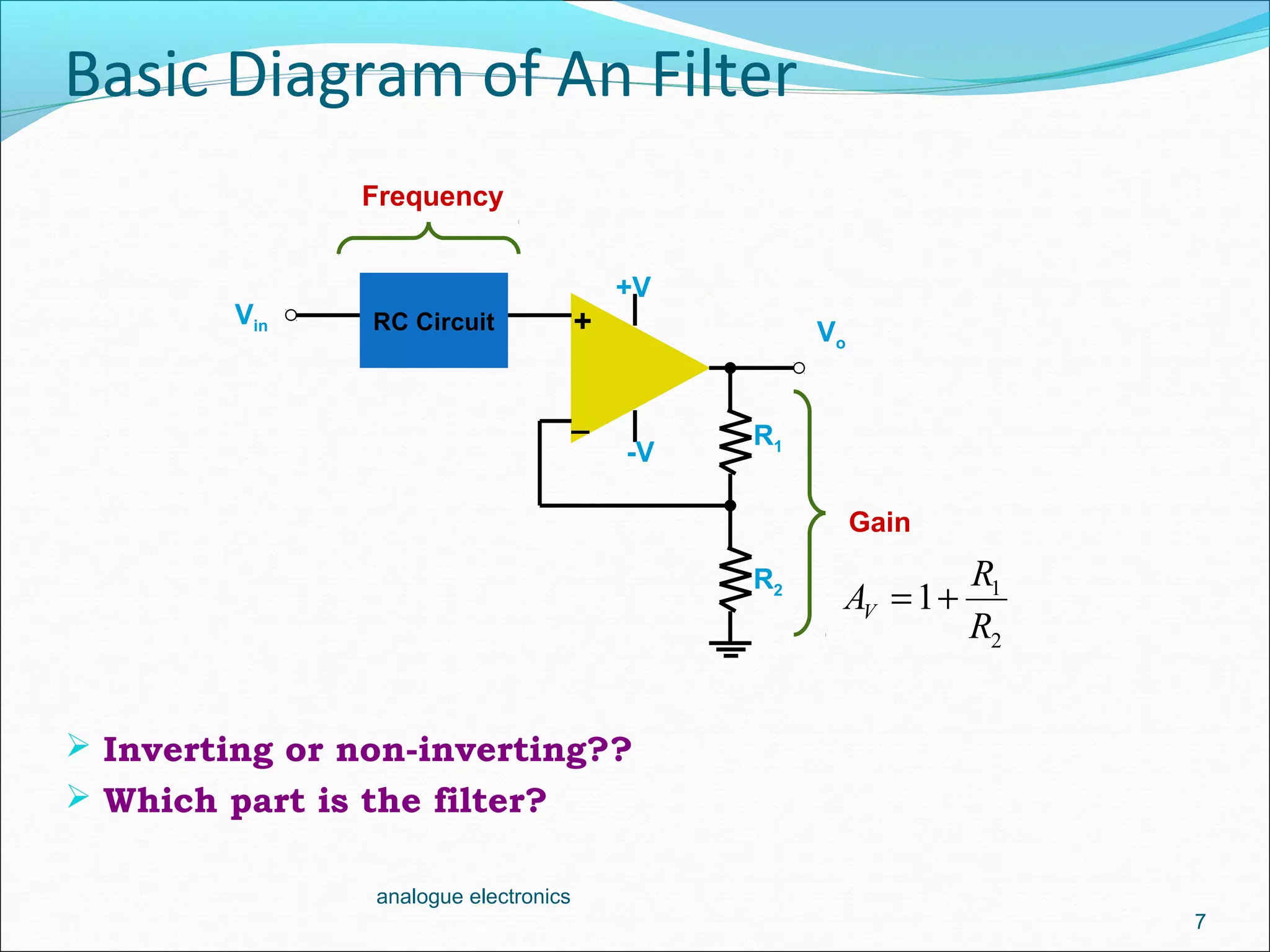
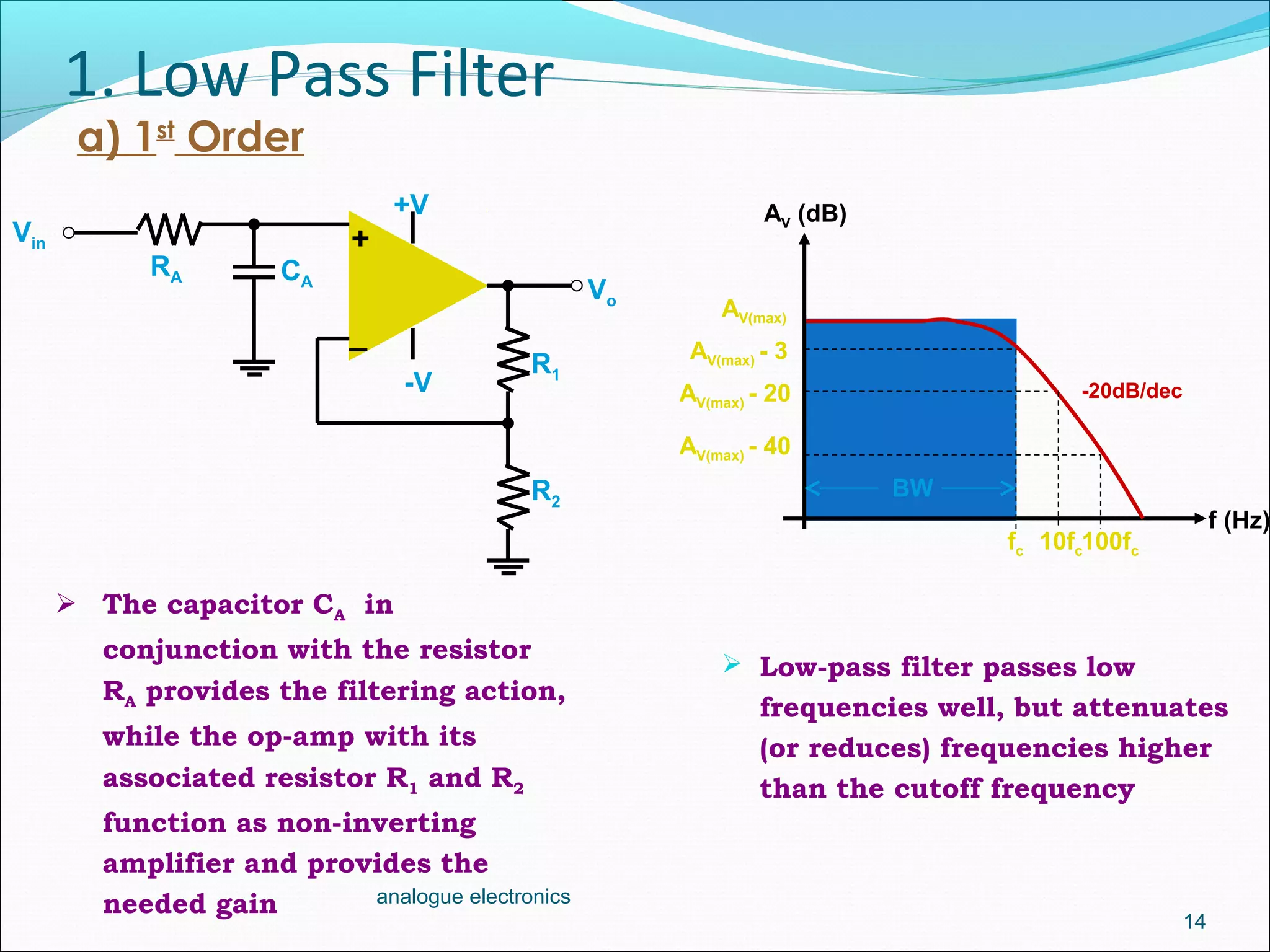
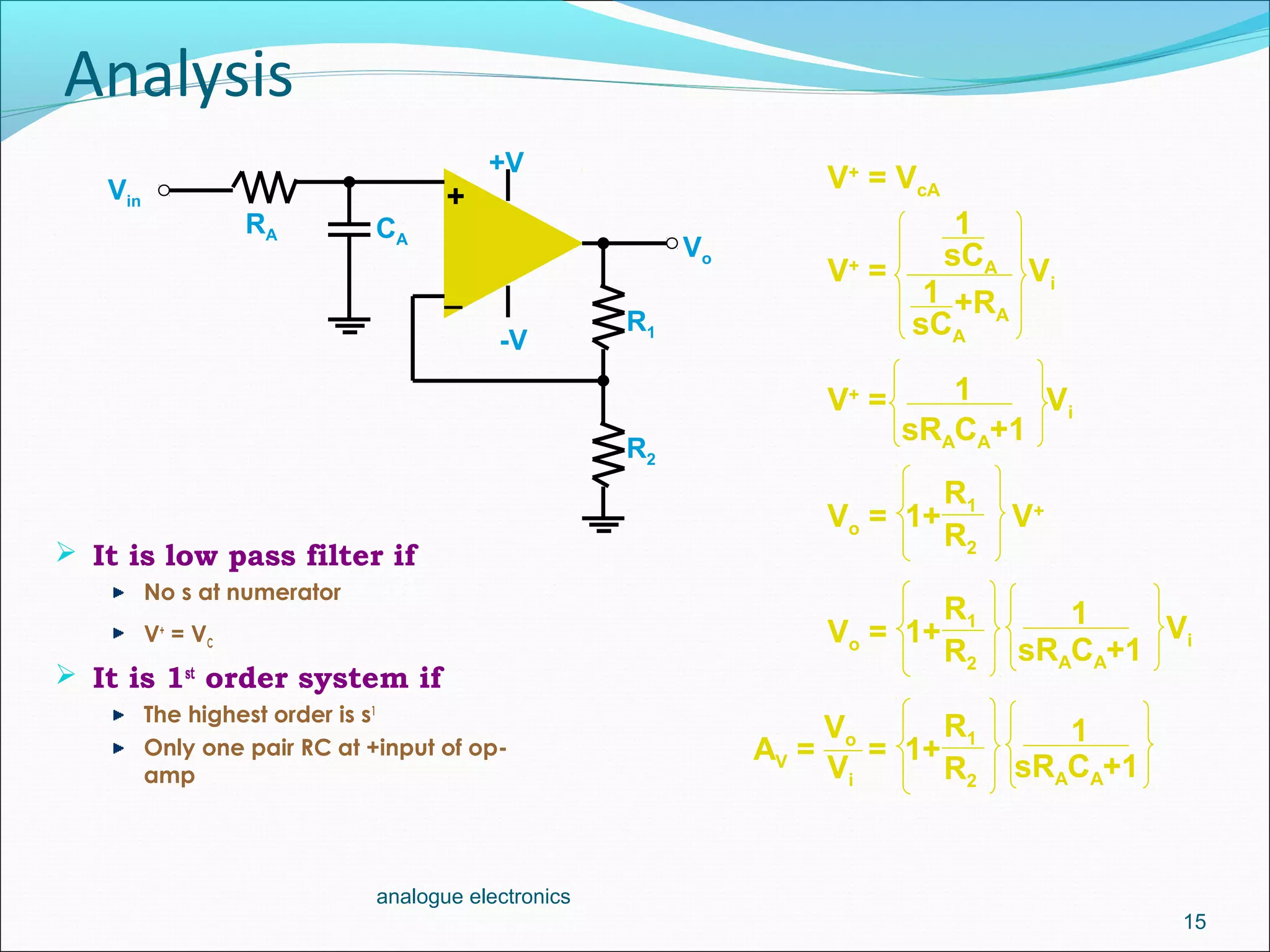
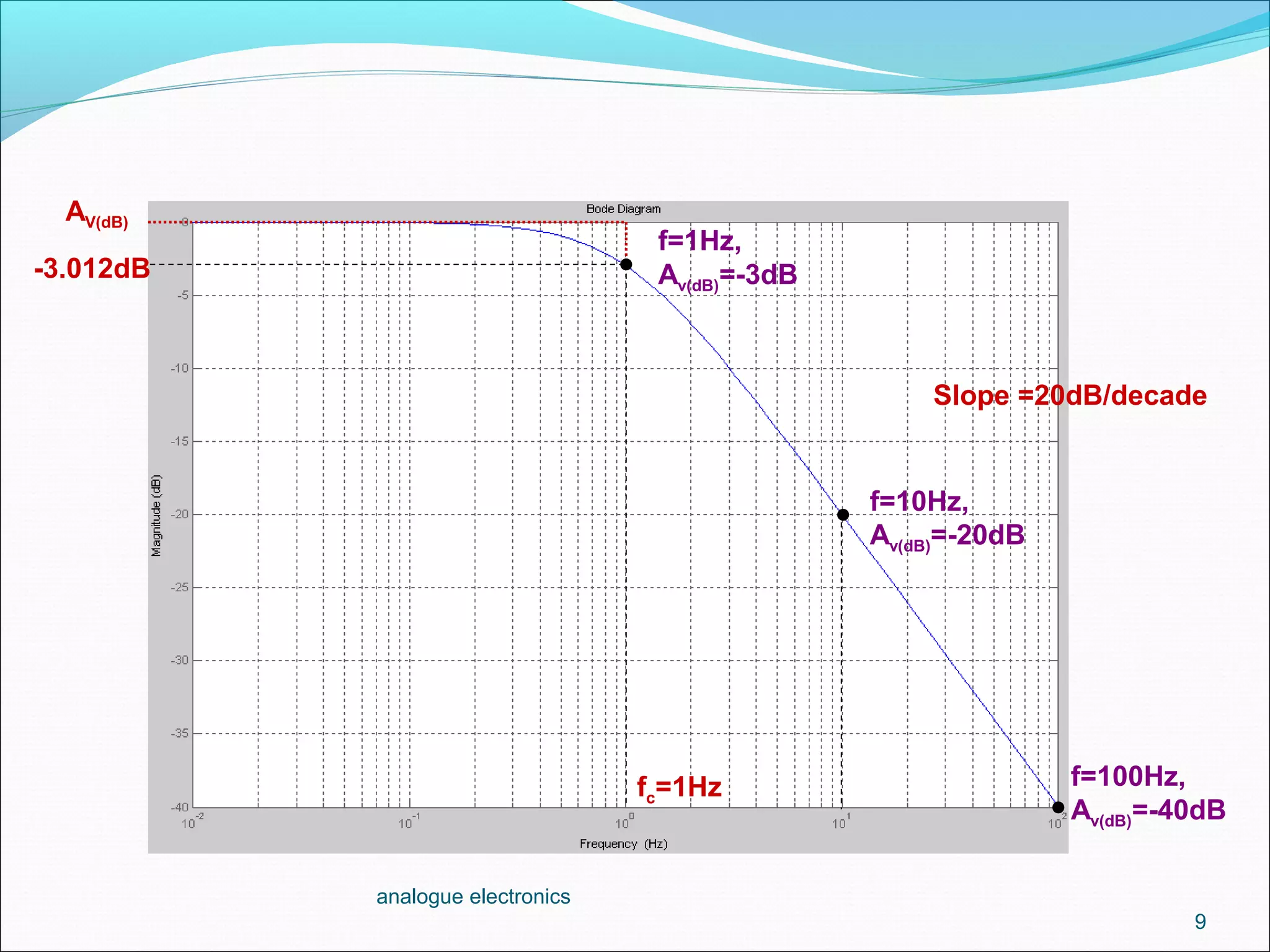
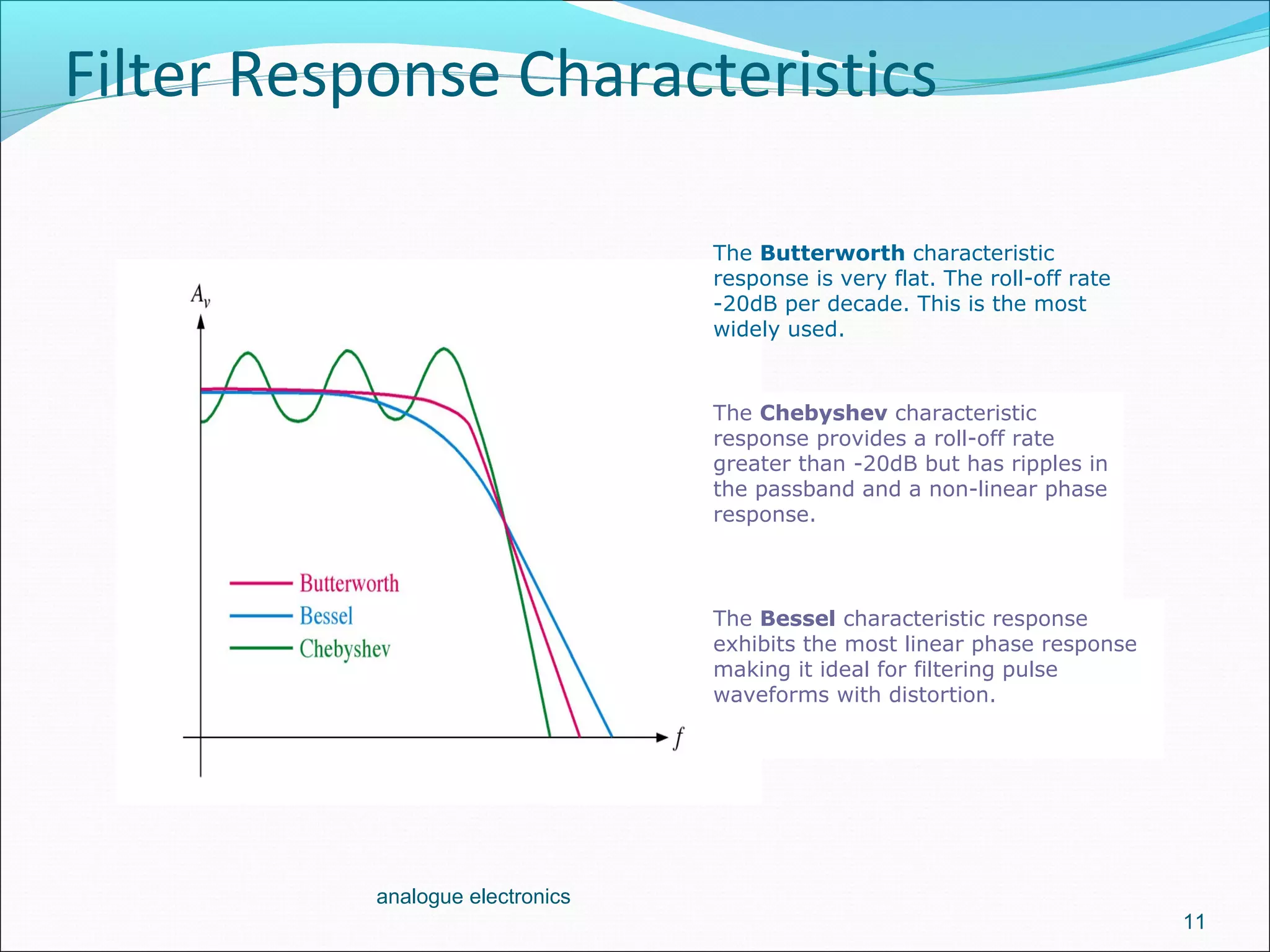
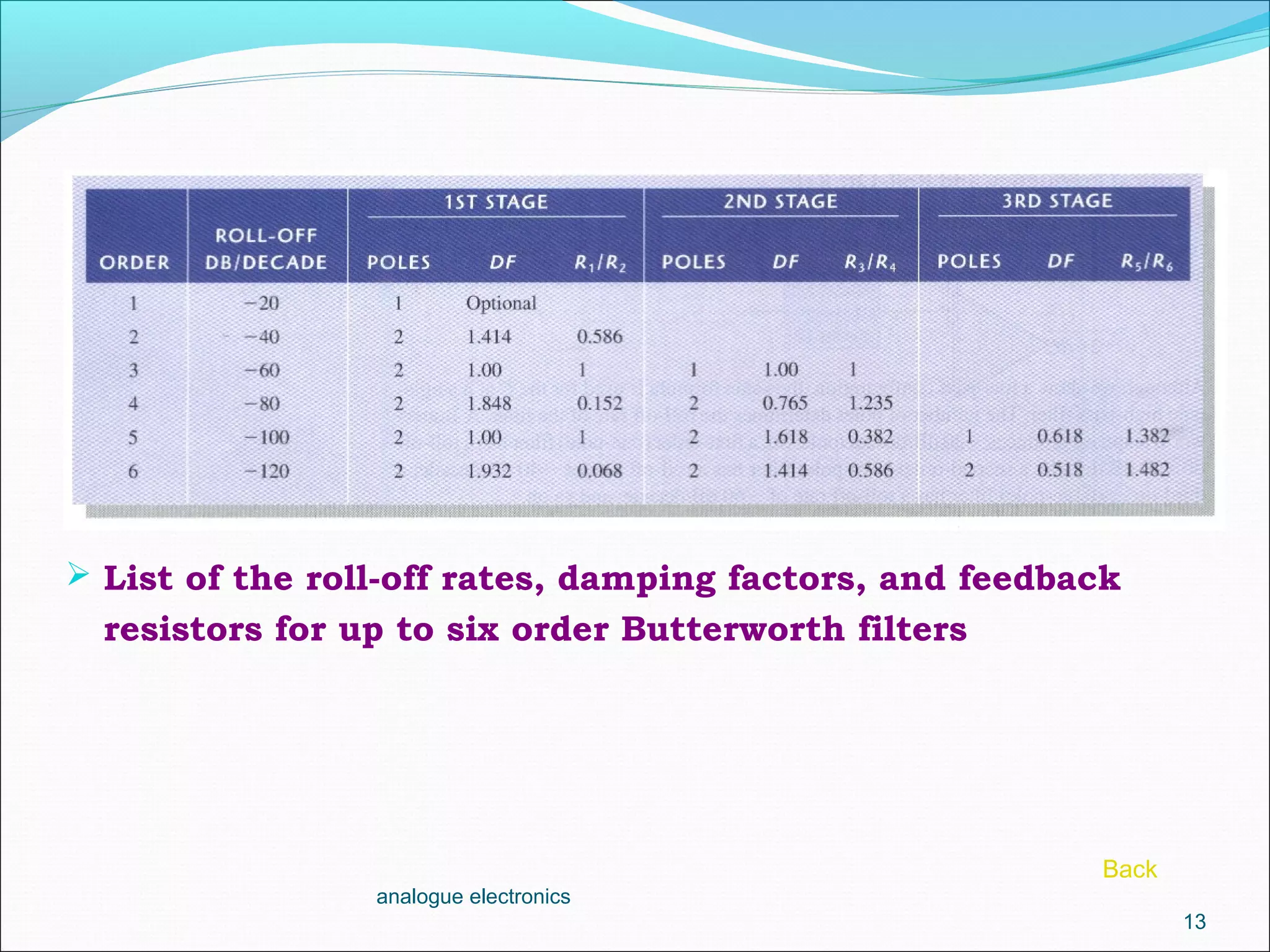
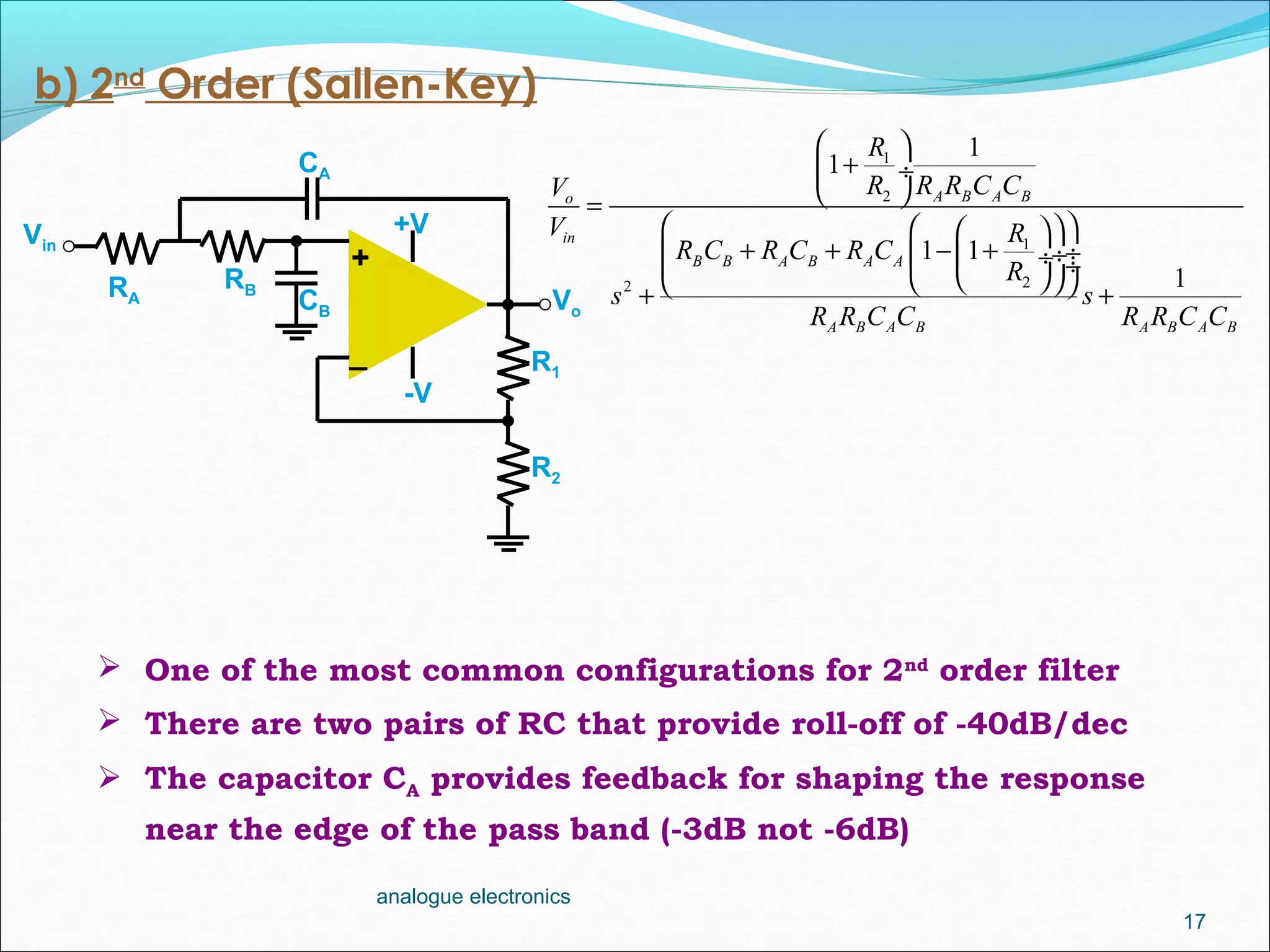
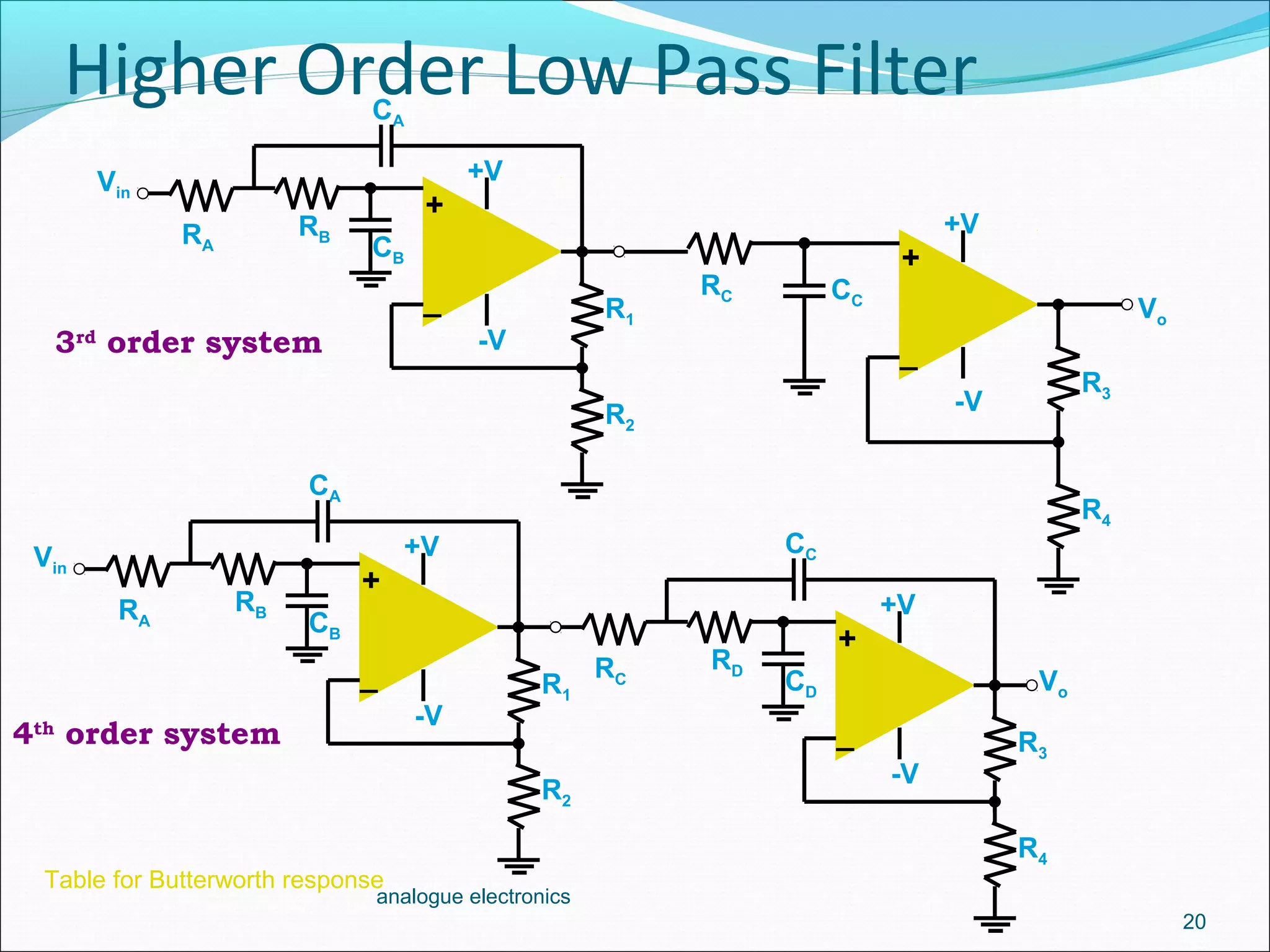
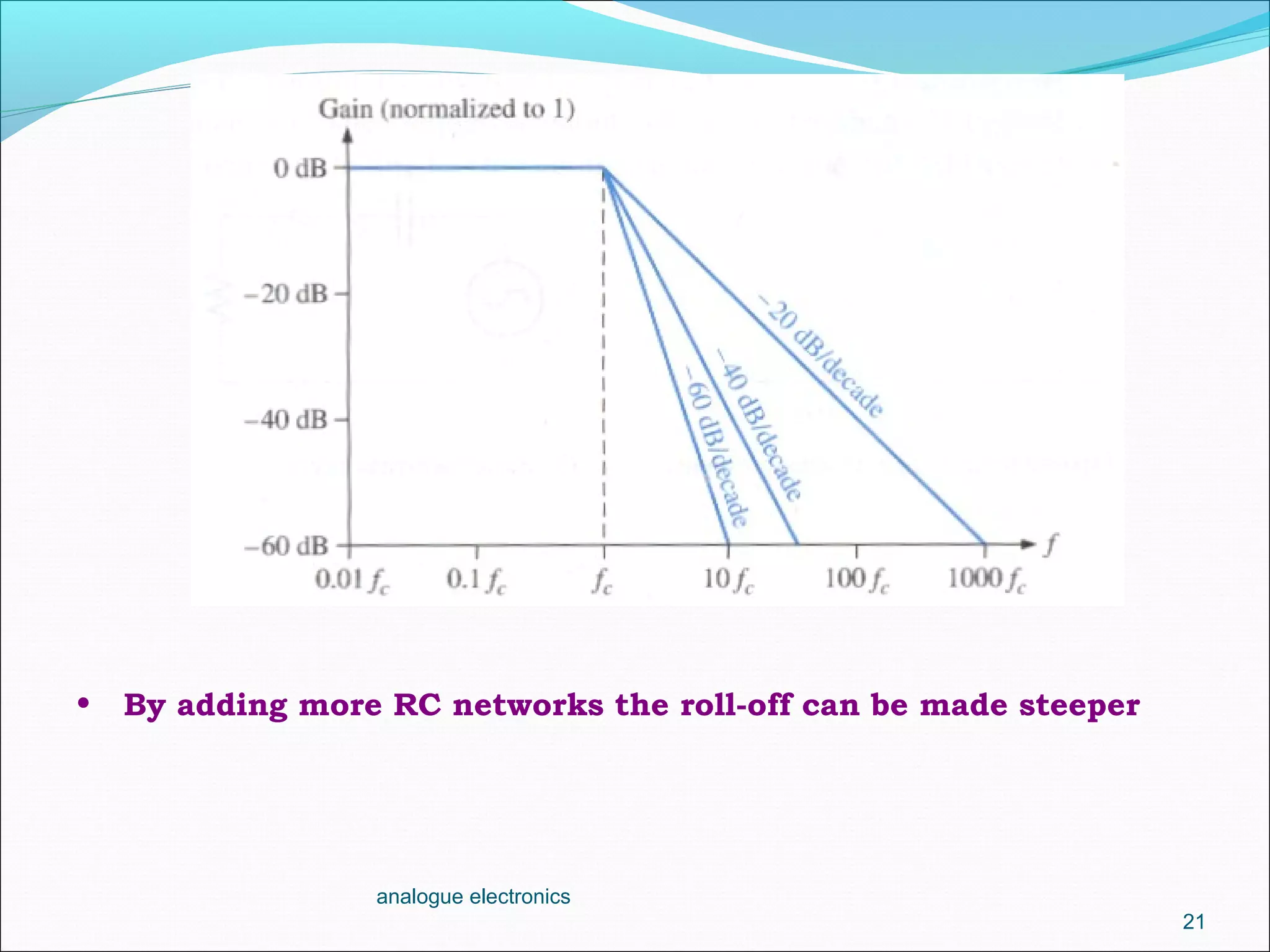
1. Low-pass filters allow low frequencies to pass through but attenuate frequencies higher than the cutoff frequency. They are implemented using a resistor and capacitor in conjunction with an op-amp amplifier. 2. A first-order low-pass filter has a single RC pair and rolls off at -20dB per decade above the cutoff frequency. Higher-order filters use multiple RC stages to achieve steeper roll-offs such as -40dB per decade for a second-order filter. 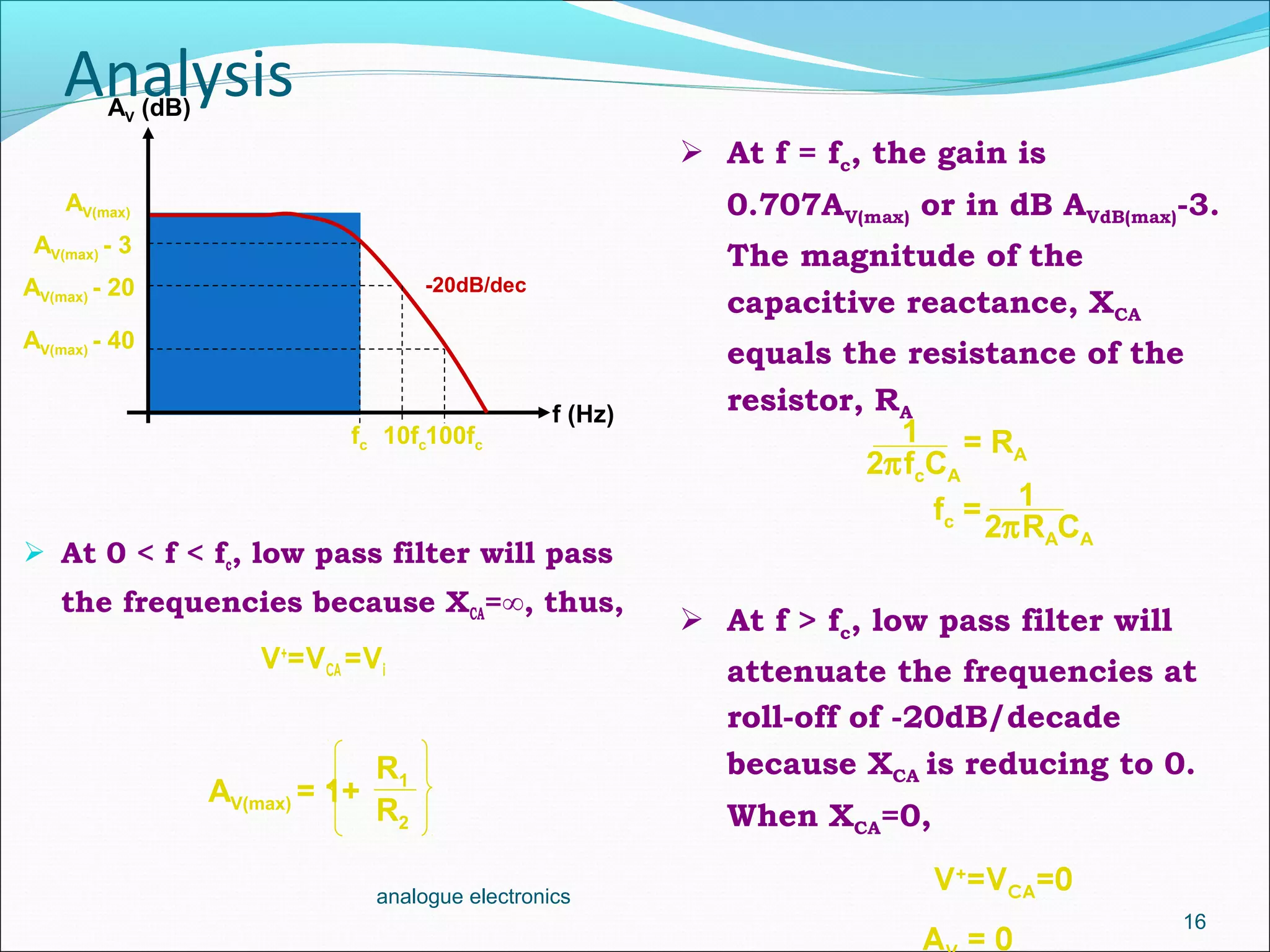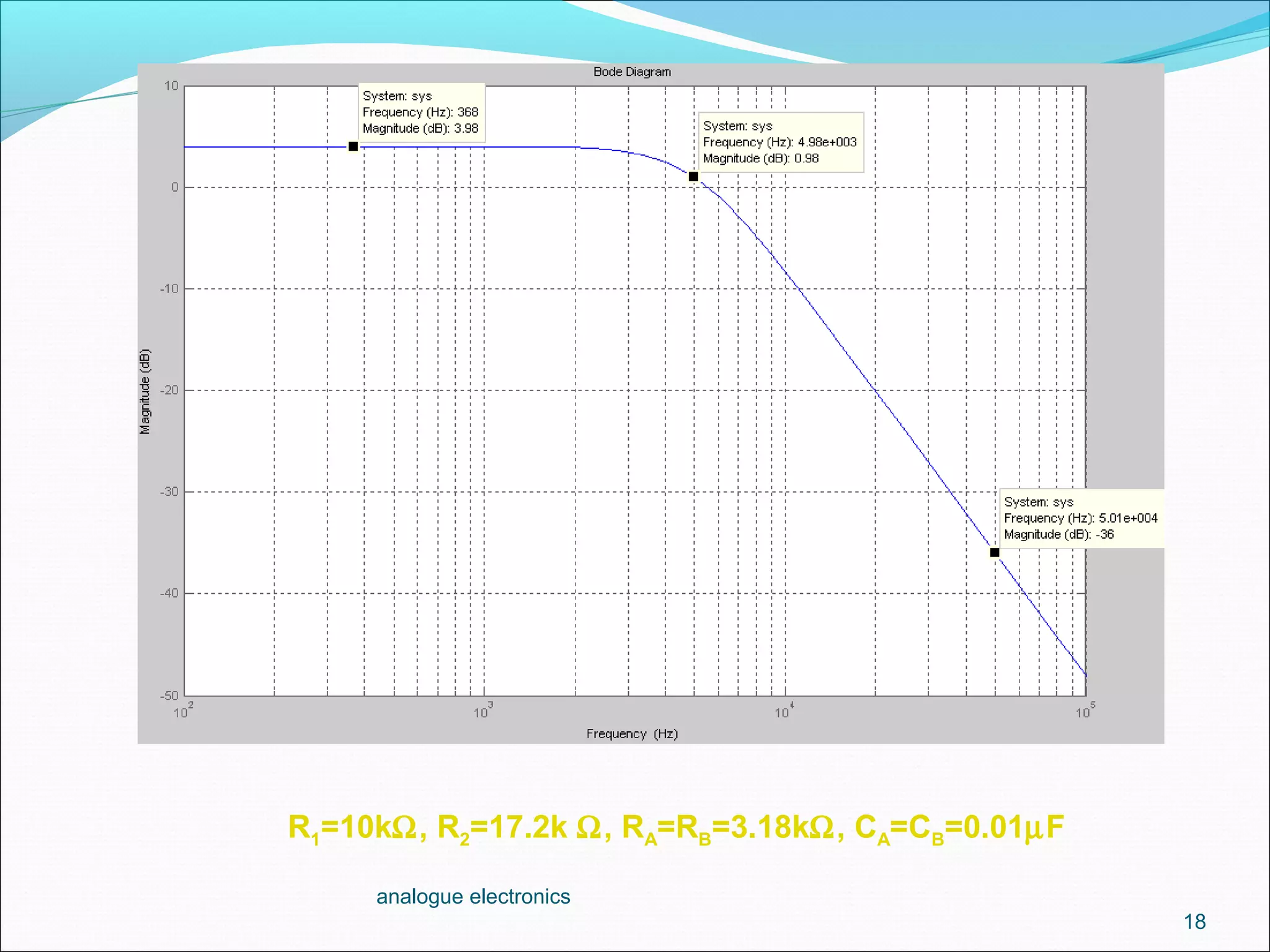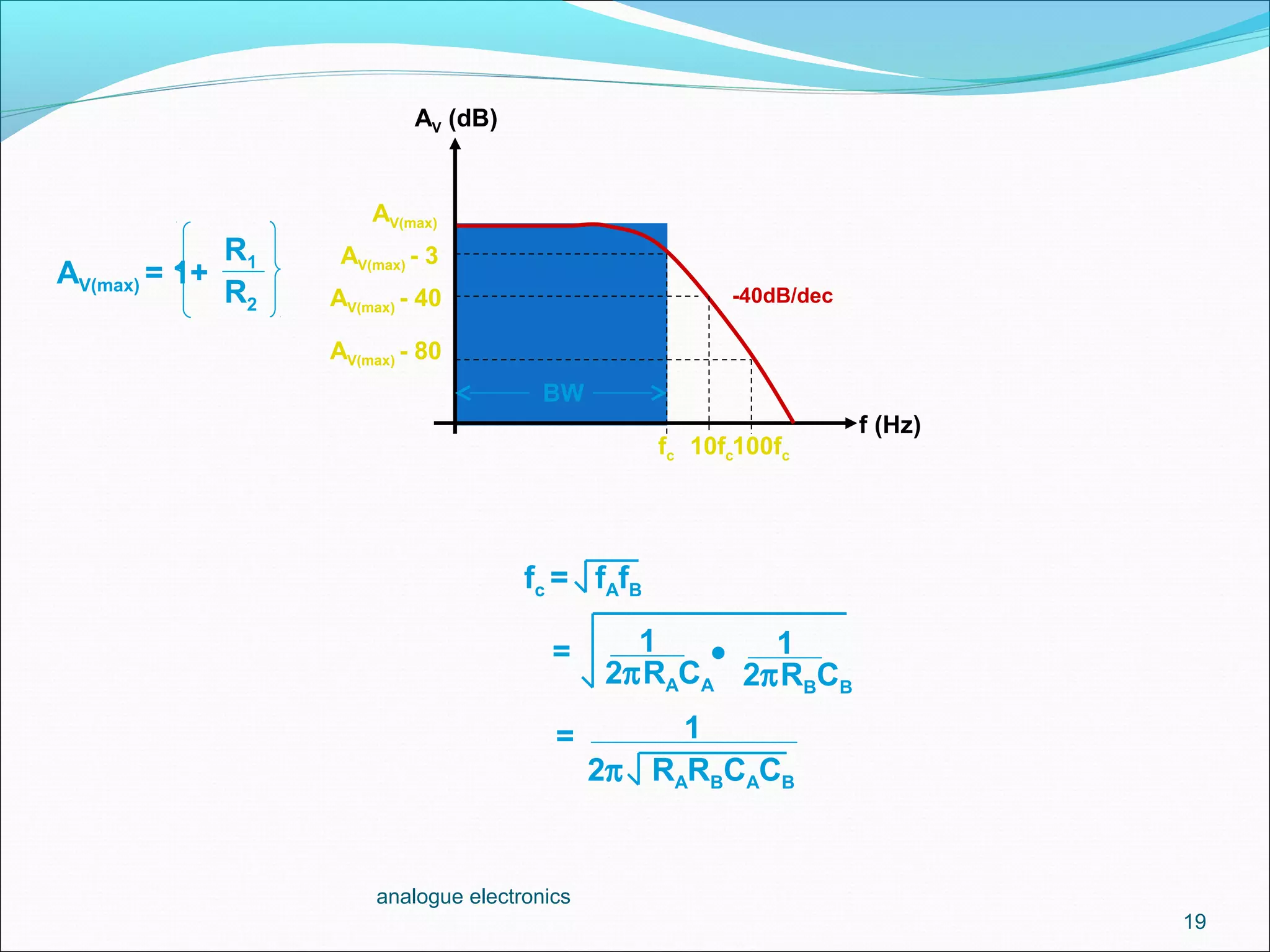3. The cutoff frequency is the frequency at which the gain is 3dB below the maximum and is inversely proportional to the product of the resistor and capacitor values in each stage.

1. CHAPTER 3: Active Filter
analogue electronics
1

2. Chapter Outcomes
2
analogue electronics
 Describe the frequency response of basic filters
 Describe the three basic filter response characteristics
 Analyze low-, high- and band-pass filters
 Design active filter

3. Introduction
PASSIVE FILTER ACTIVE FILTER
•RC, RL and RLC circuits •Active components + passive components
•Transistors or op-amps + RC/RL/RLC
•Provides frequency selectivity •Provides voltage gain
•Advantage: simple •Advantage: Loading effect is minimal
-o/p independent of the load
driven
3
analogue electronics
 Filters are circuits that are capable of passing signals with
certain selected frequencies while rejecting signals with
other frequencies
 2 types of filter

4. Introduction
Types of active filter:
Low-Pass Filter
High-Pass Filter
Bandpass Filter
o Cascaded Low-Pass and High-Pass Filter
o Multiple-Feedback Band-Pass Filter
o State-Variable Filter
o Biquad Filter
Bandstop Filter
o Multiple-Feedback Band-Stop Filter
o State-Variable Band-Stop Filter
The op-amp active filter provides controllable
cutoff frequencies and controllable gain
4
analogue electronics

5. Frequency Response
 Pass Band: The range of
frequency seen in the
filter output. Has the
same meaning as the
bandwidth (BW) of the
filter
 Stop Band: The range of
frequency blocked by the
filter. These frequency are
not see in the filter
output
5
analogue electronics
AV (dB)
f (Hz)
f (Hz)
AV (dB)
3dB
Ideal
Practical
AV (dB)
AV (dB)
f (Hz)
f (Hz)
3dB
Ideal
Practical
Pass Band
Stop Band
Transition
Region

Transition region: The
frequency between the pass
band and the stop band

Cut off Frequency : The
highest or lowest frequency
that is allowed to pass or
determines the pass band.
The cutoff frequency of real
filter is the -3 dB frequency
of that filter

6. Decibel (dB)
 This is a relative power unit. At audio frequencies a change
of one decibel (abbreviated dB) is just detectable as a change
in loudness under ideal conditions.
 For a given power ratio the decibel change is calculated as:
dB = 10 log P2/P1
 If we used voltage or current ratios instead then it becomes:
dB = 10 log (V2
2
/ R)/(V1
2
/ R)
= 20 log V2/V1
= 20 log AV
6
analogue electronics

7. Basic Diagram of An Filter
 Inverting or non-inverting??
 Which part is the filter?
7
analogue electronics
_
+Vin
R1
R2
Vo
+V
-V
RC Circuit
Gain
Frequency
1
2
1V
R
A
R
= +

8. Cut-Off Frequency
 In electronics, cut-off frequency (fc) is the frequency at
which the gain on a frequency-response plot is 3 dB less
than at mid-band gain
 The cutoff frequency often called 3-dB frequencies
 Also called the knee frequency, due to a frequency
response curve's physical appearance.
8
analogue electronics

9. 9
analogue electronics
AV(dB)
-3.012dB
fc=1Hz
Slope =20dB/decade
f=1Hz,
Av(dB)=-3dB
f=10Hz,
Av(dB)=-20dB
f=100Hz,
Av(dB)=-40dB

10. 3dB
 At -3dB, the output power is half of the output power at
pass band
10
analogue electronics
V@passband
V@passband
V@passband
20 log A -20 log 2
20 log A -10log 2
20 log A 3.012
=
=
= −
2
@
outP
out passband
V
P
R
=
2 2
@
@ 3
2 2
out passband outP outRMS
out dB
P V V
P
R R
− = = =
@ 3
2
outP
o dB outRMS
V
V V− = =
@
@ 3
2 2
V passbandoutP
V dB
in
AV
A
V
− = =

11. Filter Response Characteristics
11
analogue electronics
The Butterworth characteristic
response is very flat. The roll-off rate
-20dB per decade. This is the most
widely used.
The Chebyshev characteristic
response provides a roll-off rate
greater than -20dB but has ripples in
the passband and a non-linear phase
response.
The Bessel characteristic response
exhibits the most linear phase response
making it ideal for filtering pulse
waveforms with distortion.

12.  The damping factor of an active filter determines the type
of response characteristic
 The output signal is fed back into the filter circuit with
negative feedback determined by the combination of R1
and R2
 The negative feedback ultimately determines the type of
filter response is produced. The equation below defines
the damping factor
analogue electronics
12
DF = 2 – R1/R2

13.  List of the roll-off rates, damping factors, and feedback
resistors for up to six order Butterworth filters
13
analogue electronics
Back

14. 1. Low Pass Filter
 Low-pass filter passes low
frequencies well, but attenuates
(or reduces) frequencies higher
than the cutoff frequency
14
analogue electronics
a) 1st
Order
R1
R2
_
+Vin
+V
-V
RA CA
Vo
AV (dB)
AV(max)
AV(max) - 3
fc 10fc100fc
AV(max) - 20
AV(max) - 40
-20dB/dec
f (Hz)
 The capacitor CA in
conjunction with the resistor
RA provides the filtering action,
while the op-amp with its
associated resistor R1 and R2
function as non-inverting
amplifier and provides the
needed gain
BW

15. Analysis
 It is low pass filter if
No s at numerator
V+
= VC
 It is 1st
order system if
The highest order is s1
Only one pair RC at +input of op-
amp
15
analogue electronics
Vo = 1+ V+
R1
R2
_
+Vin
+V
-V
RA CA
Vo
V+
= Vi
1
sCA
1
sCA
+RA
R1
R2
Vo = 1+
R1
R2
Vi
V+
= Vi
1
sRACA+1
1
V+
= VcA
AV = = 1+
R1
R2Vi
1Vo
sRACA+1
sRACA+1

16. Analysis
 At 0 < f < fc, low pass filter will pass
the frequencies because XCA=∞, thus,
V+
=VCA =Vi
16
analogue electronics
AV (dB)
AV(max)
AV(max) - 3
fc 10fc100fc
AV(max) - 20
AV(max) - 40
-20dB/dec
f (Hz)
AV(max) = 1+
R1
R2
 At f = fc, the gain is
0.707AV(max) or in dB AVdB(max)-3.
The magnitude of the
capacitive reactance, XCA
equals the resistance of the
resistor, RA
 At f > fc, low pass filter will
attenuate the frequencies at
roll-off of -20dB/decade
because XCA is reducing to 0.
When XCA=0,
V+
=VCA=0
A = 0
1
2πfcCA
= RA
fc = 1
2πRACA

17. 17
analogue electronics
b) 2nd
Order (Sallen-Key)
 One of the most common configurations for 2nd
order filter
 There are two pairs of RC that provide roll-off of -40dB/dec
 The capacitor CA provides feedback for shaping the response
near the edge of the pass band (-3dB not -6dB)
Vo
R1
R2
_
+
Vin
+V
-V
RA
CA
RB
CB
1
2
1
22
1
1
1 1
1
A B A Bo
in
B B A B A A
A B A B A B A B
R
R R R C CV
V R
R C R C R C
R
s s
R R C C R R C C
 
+ ÷
 =
   
+ + − + ÷ ÷ ÷ ÷   + +

18. analogue electronics
18
R1=10kΩ, R2=17.2k Ω, RA=RB=3.18kΩ, CA=CB=0.01µF

19. 19
analogue electronics
AV (dB)
AV(max)
AV(max) - 3
fc 10fc100fc
AV(max) - 40
AV(max) - 80
-40dB/dec
f (Hz)
BW
AV(max) = 1+
R1
R2
1
2π RARBCACB
fc = fAfB
1
2πRACA
1
2πRBCB
•=
=

20. Higher Order Low Pass Filter
20
analogue electronics
R1
R2
_
+
Vin
+V
-V
RA
CA
RB
CB
R3
R4
_
+
+V
-V
RC CC
Vo
R1
R2
_
+
Vin
+V
-V
RA
CA
RB
CB
Vo
R3
R4
_
+
+V
-V
RC
CC
RD
CD
Table for Butterworth response
3rd
order system
4th
order system

21. analogue electronics
21
• By adding more RC networks the roll-off can be made steeper