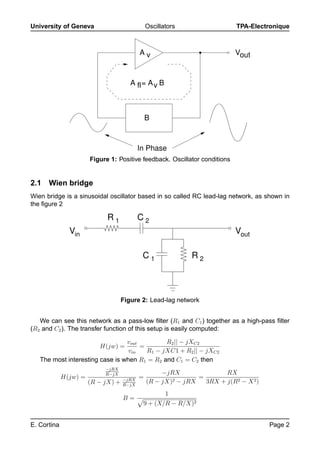
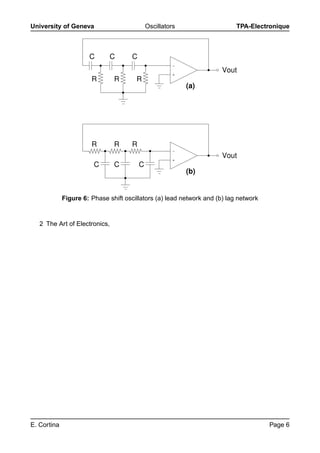
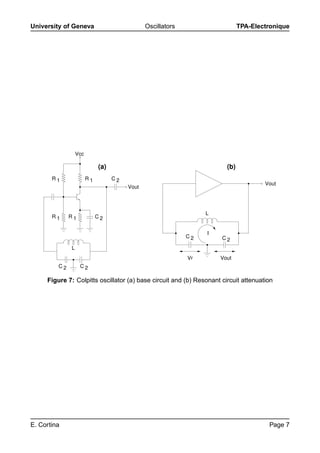
This document discusses different types of oscillators, including RC oscillators and LC oscillators. RC oscillators are useful for frequencies up to 1 MHz and include Wien bridge, phase-shift, and double T-filter oscillators. LC oscillators are better for higher frequencies above 1 MHz due to limitations of opamps. Specific oscillator circuits are described, including the Wien bridge configuration and conditions for oscillation. The Colpitts oscillator uses transistors for amplification at higher frequencies.

1. University of Geneva Oscillators TPA-Electronique
Oscillators
Contents
1 Introduction 1
2 RC oscillators 1
2.1 Wien bridge . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
2.2 Phase-shift oscillator . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
2.3 Double T-filter oscillator . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
3 LC oscillators 4
3.1 Colpitts Oscillator . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
4 Biliography 5
1 Introduction
Oscillators are circuits that produce a repetitive waveform with only a DC voltage at the
output. The output waveform can be sinusoidal, rectangular, triangular, etc. At the base of
almost any oscillator there is an amplification stage with a positive feedback circuit that will
produce a phase shift and an attenuation.
Positive feedback consist in the redirecting of the output signal to the input stage of the
amplifier without a phase shift. This feedback signal is then amplified again generating the
output signal, that produces the feedback signal. This phenomenon, in wich the output signal
“takes care”of itself in order to generate continuum signal is called oscillation.
Two conditions then should be fulfilled to have an stable oscillator:
1. The phase shift of the feedback loop should be 0
2. The overall gain of the feeddback loop should be 1
In order to arrive to the stable regime of the oscillator, during the starting period the gain
of the feedback loop should be greater than one, to allow the amplitude of the output signal
to achieve the desired level. Once this amplitude has been reached, the overall gain should
goes down again to one. The very first oscillations are generated by trasitory reactions and
noises once the power is switched on. The feedback circuit should be designed to amplify
just a single frequency, and the relatively faint signal picked up from transitories and noise is
then used to startup the oscillator
2 RC oscillators
This type of oscillators, use RC elements in the feedback branch. Useful to frequencies up
to 1 MHz.
E. Cortina Page 1

2. University of Geneva Oscillators TPA-Electronique
Av Vout
A fl = A v B
B
In Phase
Figure 1: Positive feedback. Oscillator conditions
2.1 Wien bridge
Wien bridge is a sinusoidal oscillator based in so called RC lead-lag network, as shown in
the figure 2
R1 C2
Vin Vout
C1 R2
Figure 2: Lead-lag network
We can see this network as a pass-low filter (R1 and C1 ) together as a high-pass filter
(R2 and C2 ). The transfer function of this setup is easily computed:
vout R2 || − jXC2
H(jw) = =
vin R1 − jXC1 + R2 || − jXC2
The most interesting case is when R1 = R2 and C1 = C2 then
−jRX
R−jX −jRX RX
H(jw) = −jRX
= 2 − jRX
=
(R − jX) + R−jX
(R − jX) 3RX + j(R2 − X 2 )
1
B=
9 + (X/R − R/X)2
E. Cortina Page 2

3. University of Geneva Oscillators TPA-Electronique
X/R − R/X
φ = arctan
3
In figure 3 are shown both the gain in tension (B) as the phase shift (φ) as a function of
the frequency. The oscillating frequency is
1
fr =
2πRC
and for this frequency we have that B = 1/3 and φ = 0o . This means that the amplifier
should have a gain A = 3 and introduce a phase shift φ = 0o /
Gain Phase shift
80
0.3
60
0.25 40
20
0.2
0
0.15
-20
0.1 -40
-60
0.05
-80
0 -2 -1 -2 -1
10 10 1 10 10 10 1 10
Frequency (au) Frequency (au)
Figure 3: Lead-lag network gain and phase shift for RC = 1/2π
In the figure 4 is shown the base schematics of a Wien oscillator, based in an opamp.
The positive feedback is created by the lead-jag network, and the negative feedback create
a non-inverting amplifer with gain
R1
A=1+ =3 → R1 = 2R2
R2
In the beginning, the gain of the negative feedback should be greater than 3, and later,
once the output amplitude has been achieved, go back to 3. There are various methods to
accomplish it in an automatic way.
1. The most easy and classical method is to use a low power incandescende lamp instead
of R2 . When swicth on, the resistance of the lamp is small, giving an amplification
greater that 3. Once the oscillations grows in amplitude the resistance also goes up,
arriving to a value R in the desired amplitude. If the feedback resistance is chosen to
be R1 = 2R , we will obtain automatically a gain A = 3, giving the stable oscillations.
See figure 5
2. Another method consist is adding a third resistor R3 in parallel with two zener diodes
conected back to back as shown in figure ??. When switch on, the zener diodes are in
open circuit, giving then the value of the gain as:
R1 + R3 R3
A=1+ =3+
R2 R2
Once the output arrives to the zener voltage, the diodes short circuit the resistor restor-
ing the gain A = 3 and the output signal becomes stable.
E. Cortina Page 3

4. University of Geneva Oscillators TPA-Electronique
R1
−
+
Vout
R2
C R
R C
Figure 4: Wien-bridge, base setup
2.2 Phase-shift oscillator
Figure ?? shows the two configurations of the phase-shift oscillators, a phase shift oscillator.
Each of the RC circuits in the positive feedback introduces a phase shift that depend of the
actual values of R and C. Only the frequency that produces a pahse shift on each sector
equal to 90o , will be stable, so the pahse shift of is 180o , then the op-amp should work in an
inverting configuration with gain 1. The frequency that fullfill this condition is:
1
fr = √
2πRC 6
2.3 Double T-filter oscillator
3 LC oscillators
RC oscillators are good for frequencies up to 1 MHz, but for higher frequencies, LC oscilla-
tors are better. Due to the limited bandwidth of most of opamps the amplification is based
on discrete BJT transistors.
3.1 Colpitts Oscillator
The resonance frequence of this circuit (see figure 7-a) is the resonance frequence of the
LC circuit:
1 C1 C2
fr ≈ √ → CT =
2π LCT C1 + C2
E. Cortina Page 4

5. University of Geneva Oscillators TPA-Electronique
2R’ R1 R3
− −
+
Vout +
Vout
R2
R’
C R C R
R C R C
(a) (b)
Figure 5: Wien-bridge (a) with lamp, (b)
The gain of the feedback circuit depend of the values of the capacitors, (see figure 7-b)
Vr IXC1 XC1 1/2πfr C1 C2
B= = = = =
Vout IXC 2 XC 2 1/2πfr C2 C1
Then the amplifier gain should be
C2
A=
C1
In the common emitter configuration shown in the example, the gain is
rC
A=
re
But this expression is valid only for low frequencies, with higher frequencies the lag networks
in base and collector can distort, and even kill the oscillation. Indeed the actual value of A
depend on the bandwidth of the transistor. If the cut frequencies of these networks are
bigger than oscillation frequency, the gain is the quoted in the previous expression. If the
oscillation frequency is larger than the cut frequency then the gain is significantly lower that
rC /re that togheter with the phase shifts introduced will kill the oscillation.
Another thing to take into account is the effect of the input impedance of the the am-
plification. Input impedance is part of the load of the resonant circuit, and can reduce the
Q factor of this circuit, then the resonant frequency change accordingly with the following
expression:
1 Q2
fr = √
2π LCT Q2 + 1
In case ofQ > 10 (most of the cases) the effect is less than 1%, and this effect can be
ignored, but in order to minimize the effect of the input impedance, we can replace BJT
transistor by a FET, with input impedance much larger than in BJT . In case that the load of
the circuit is too low, the Q factor can be also reduced. To avoid this a transformer coupling
that will increase the load impedance is adviced.
4 Biliography
1 Electronique, Thomas L. Floyd, Ed. Reynald Goulet (1999)
E. Cortina Page 5

6. University of Geneva Oscillators TPA-Electronique
C C C
−
+
Vout
R R R
(a)
R R R
−
+
Vout
C C C
(b)
Figure 6: Phase shift oscillators (a) lead network and (b) lag network
2 The Art of Electronics,
E. Cortina Page 6

7. University of Geneva Oscillators TPA-Electronique
Vcc
(a) (b)
R1 R1 C2
Vout
Vout
L
R1 R1 C2
I
C2 C2
L
Vr Vout
C2 C2
Figure 7: Colpitts oscillator (a) base circuit and (b) Resonant circuit attenuation
E. Cortina Page 7