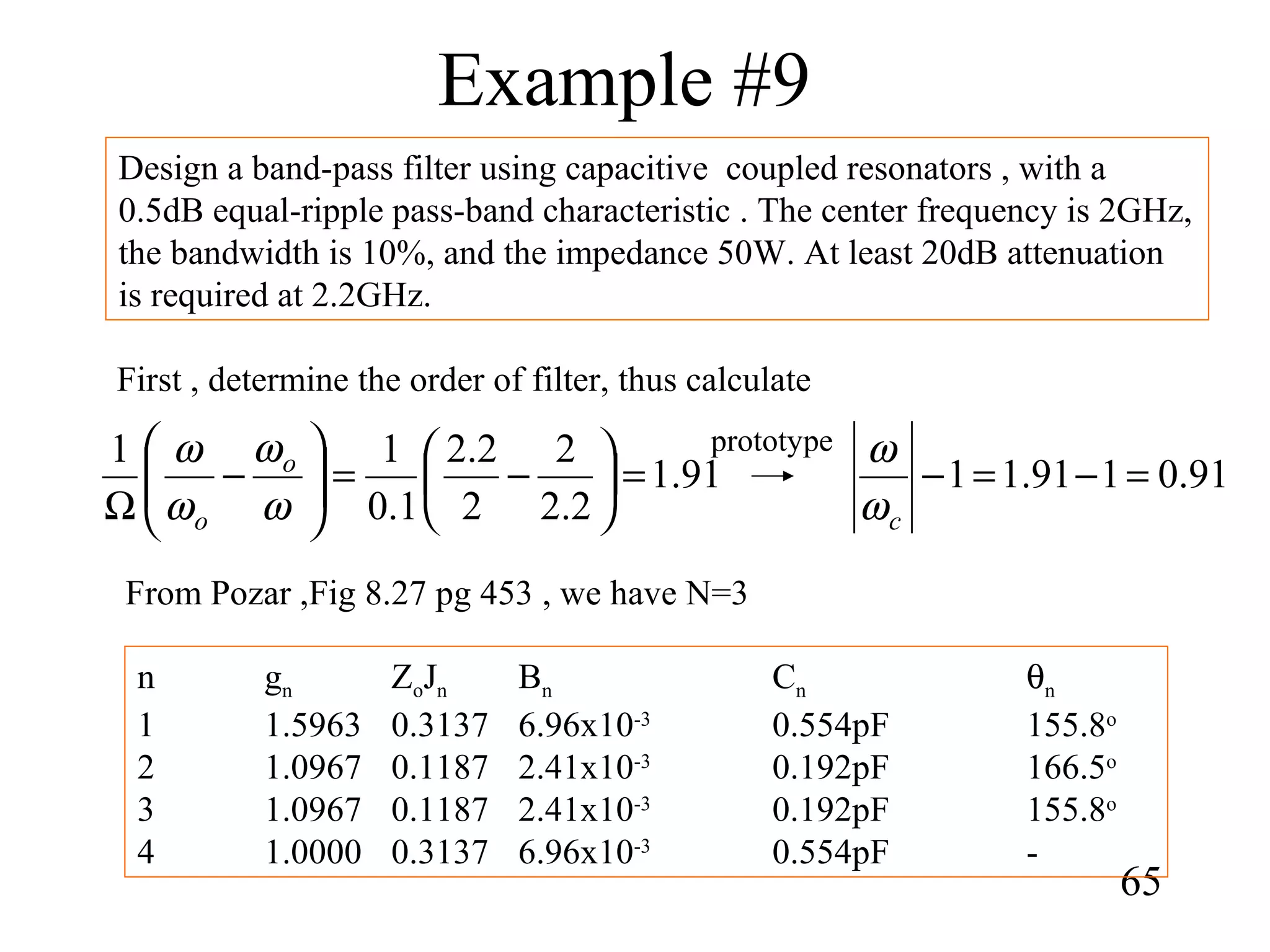
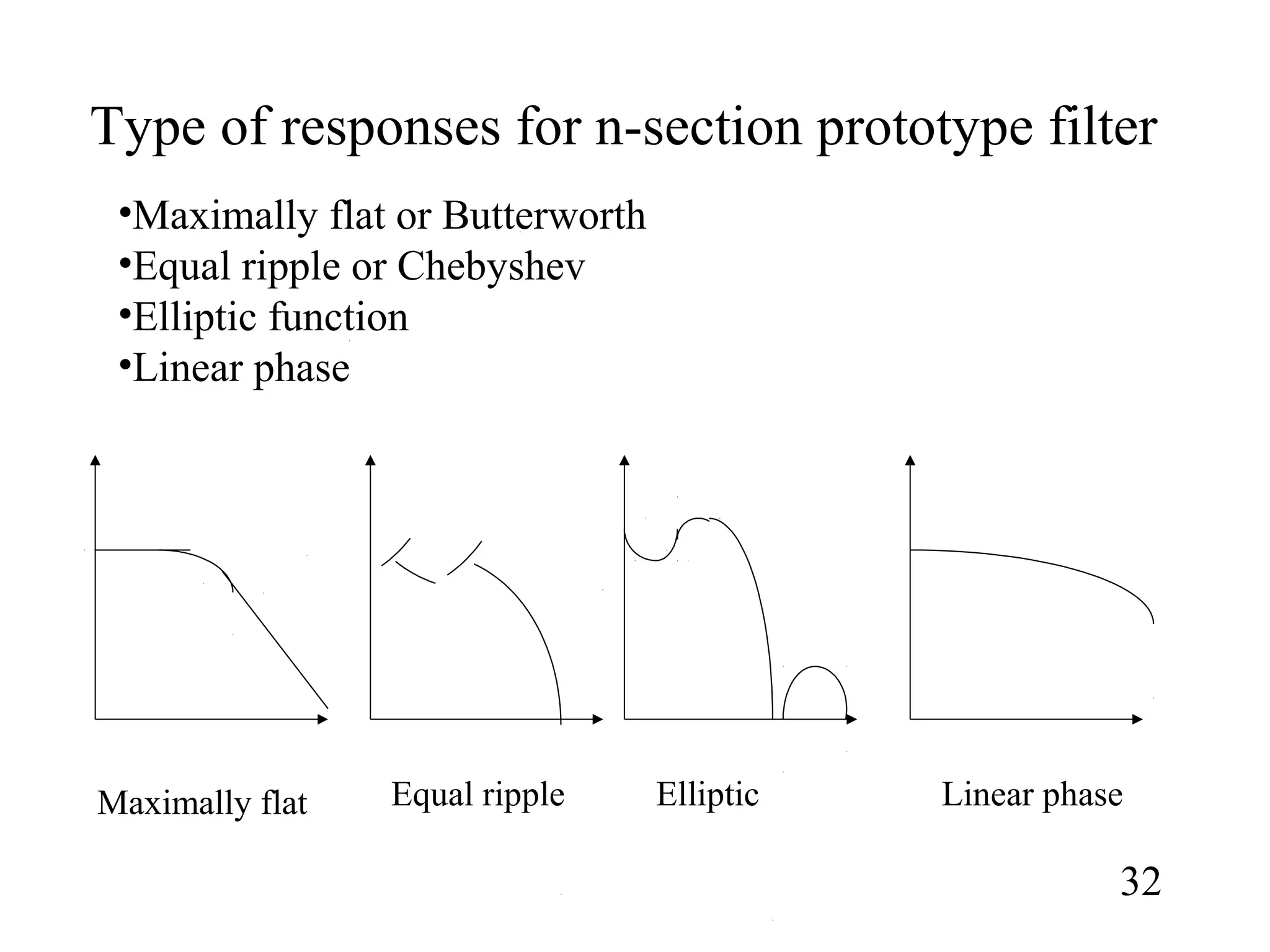
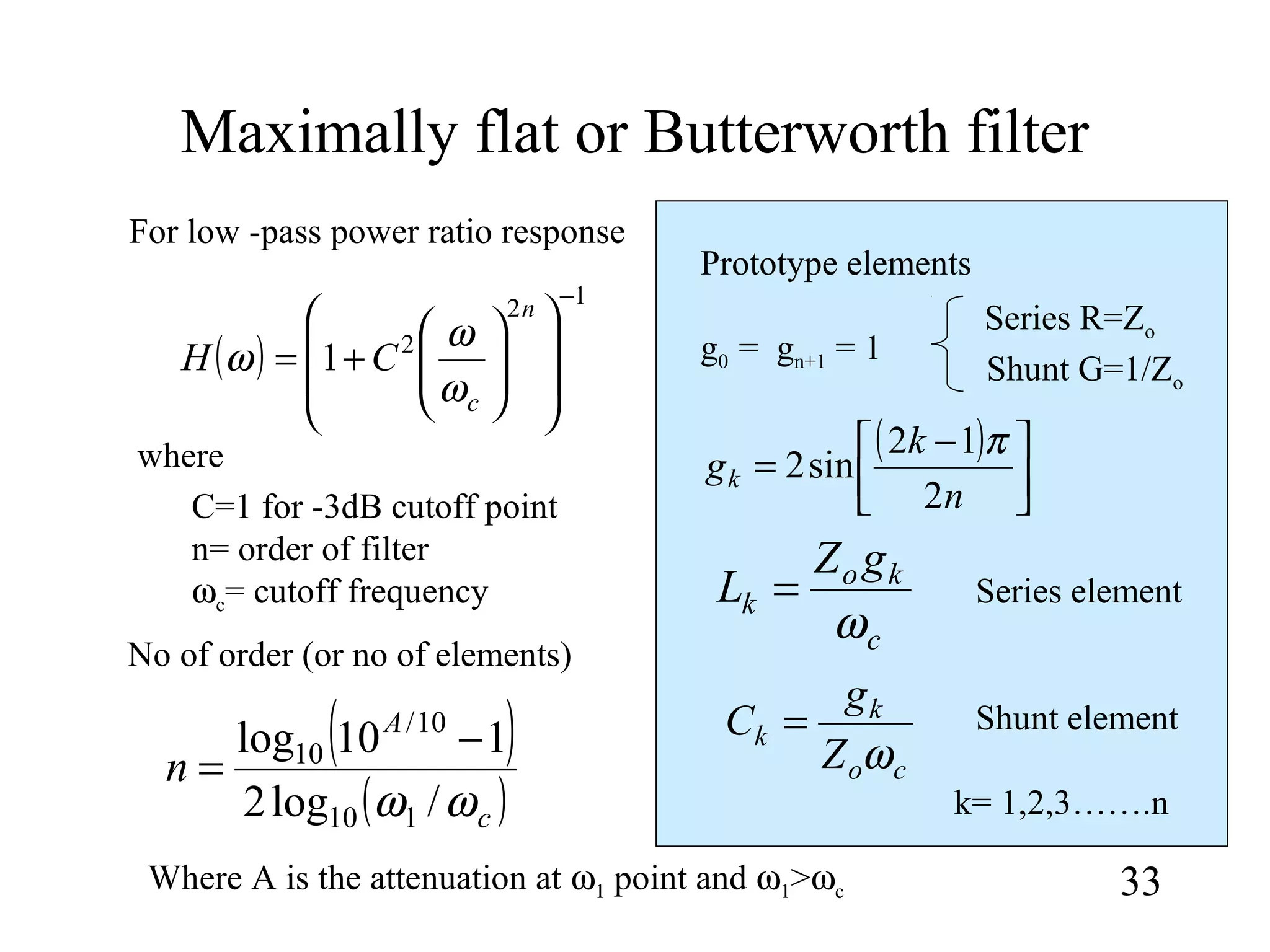
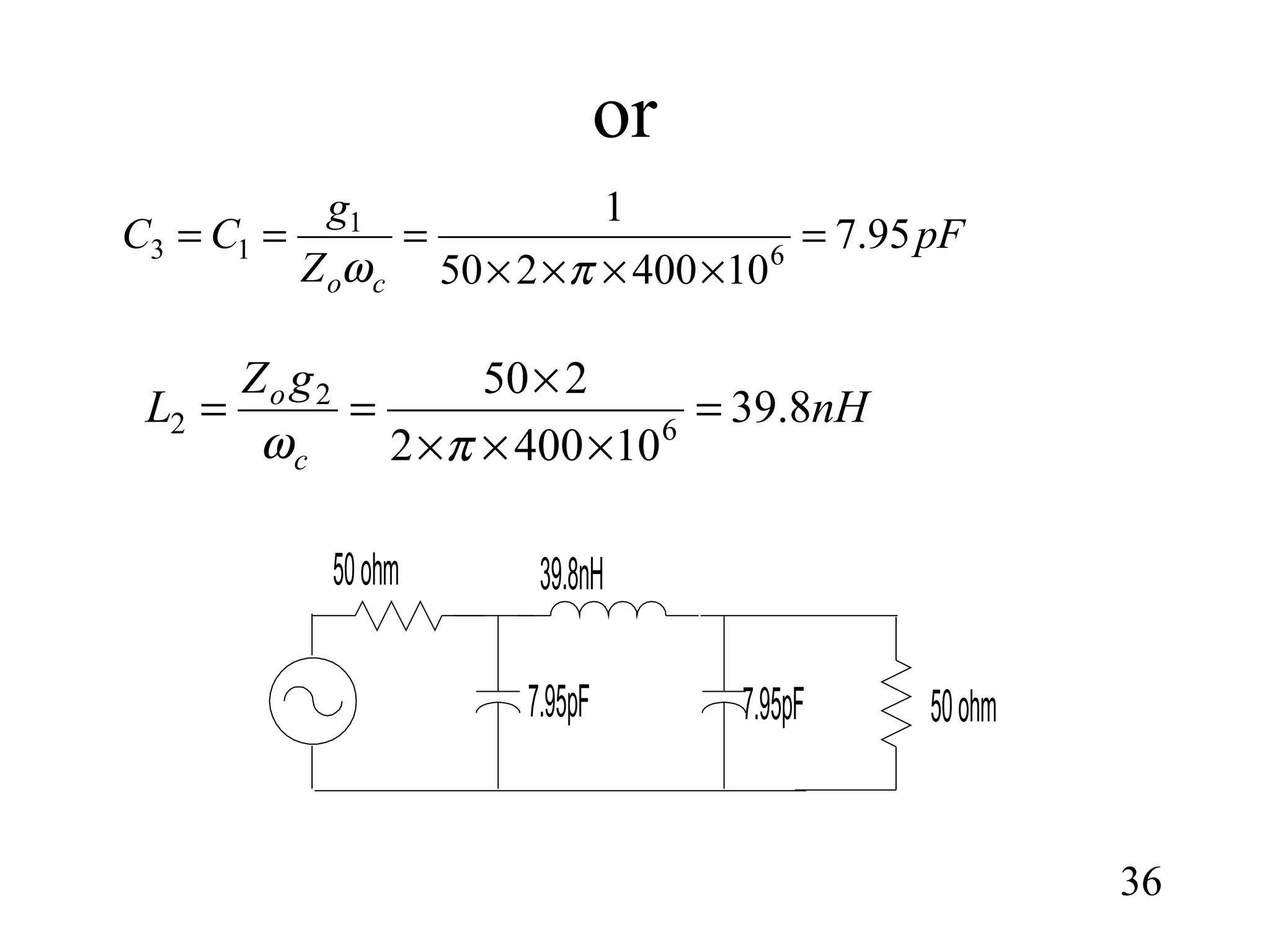
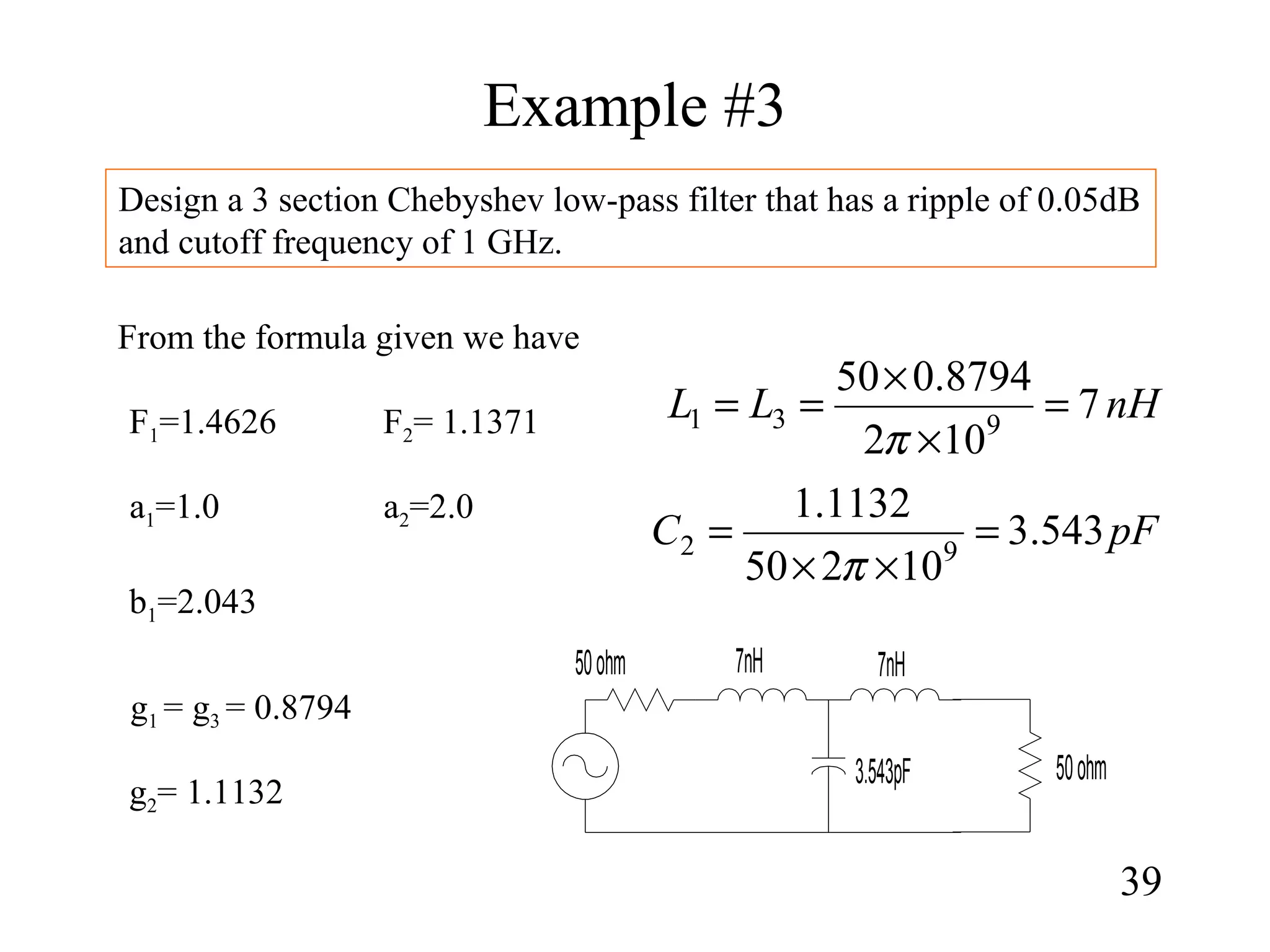
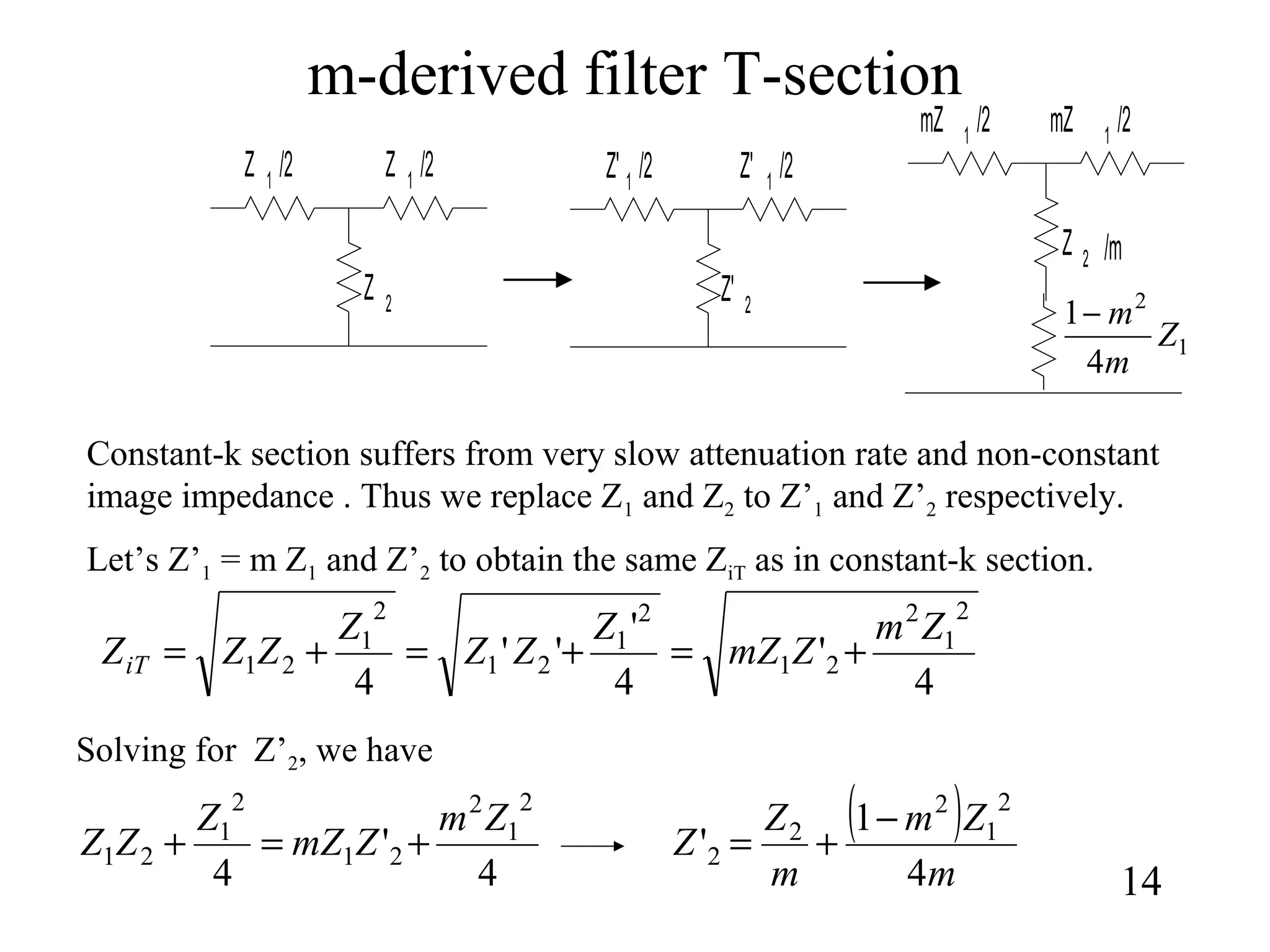
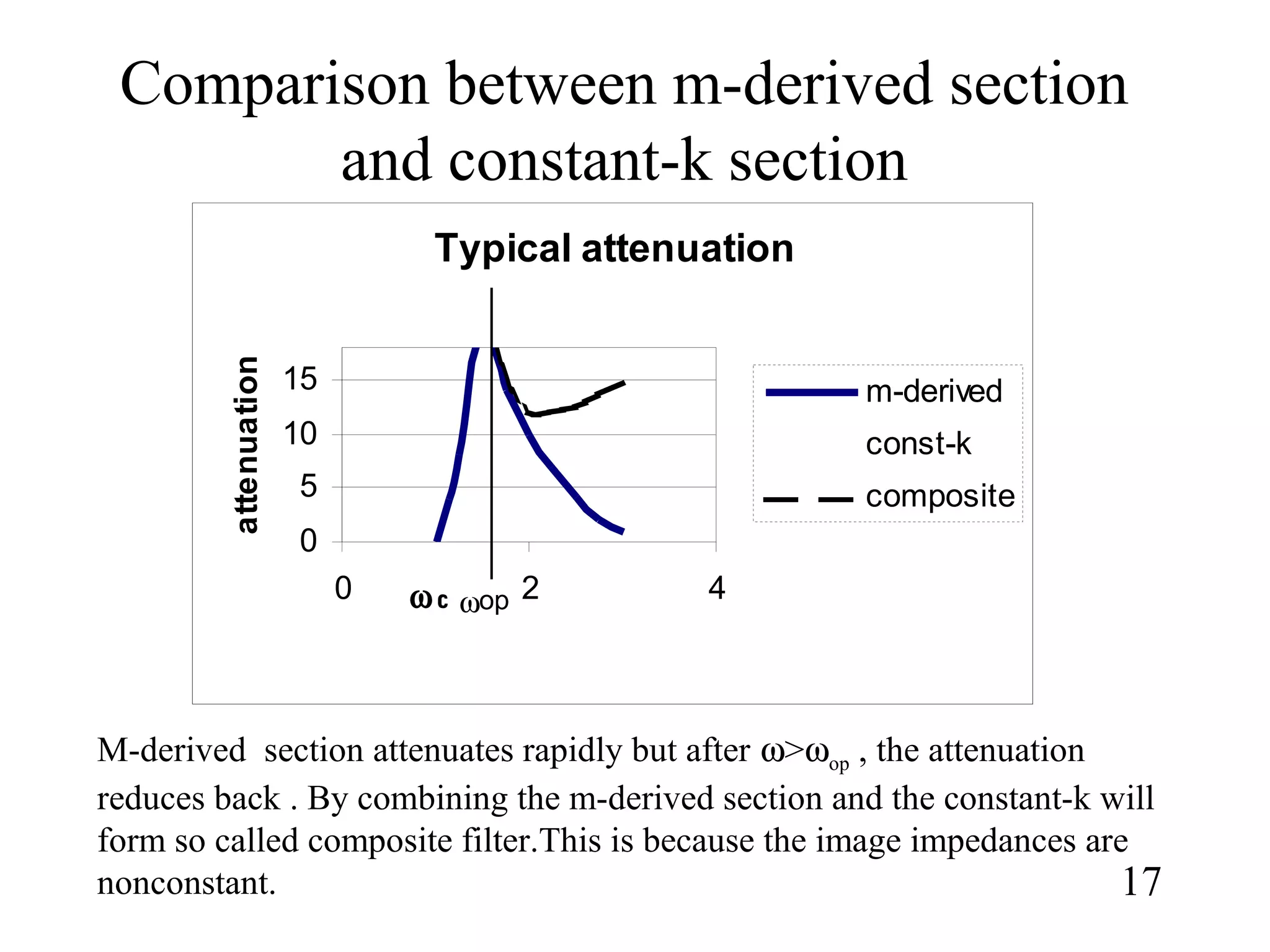
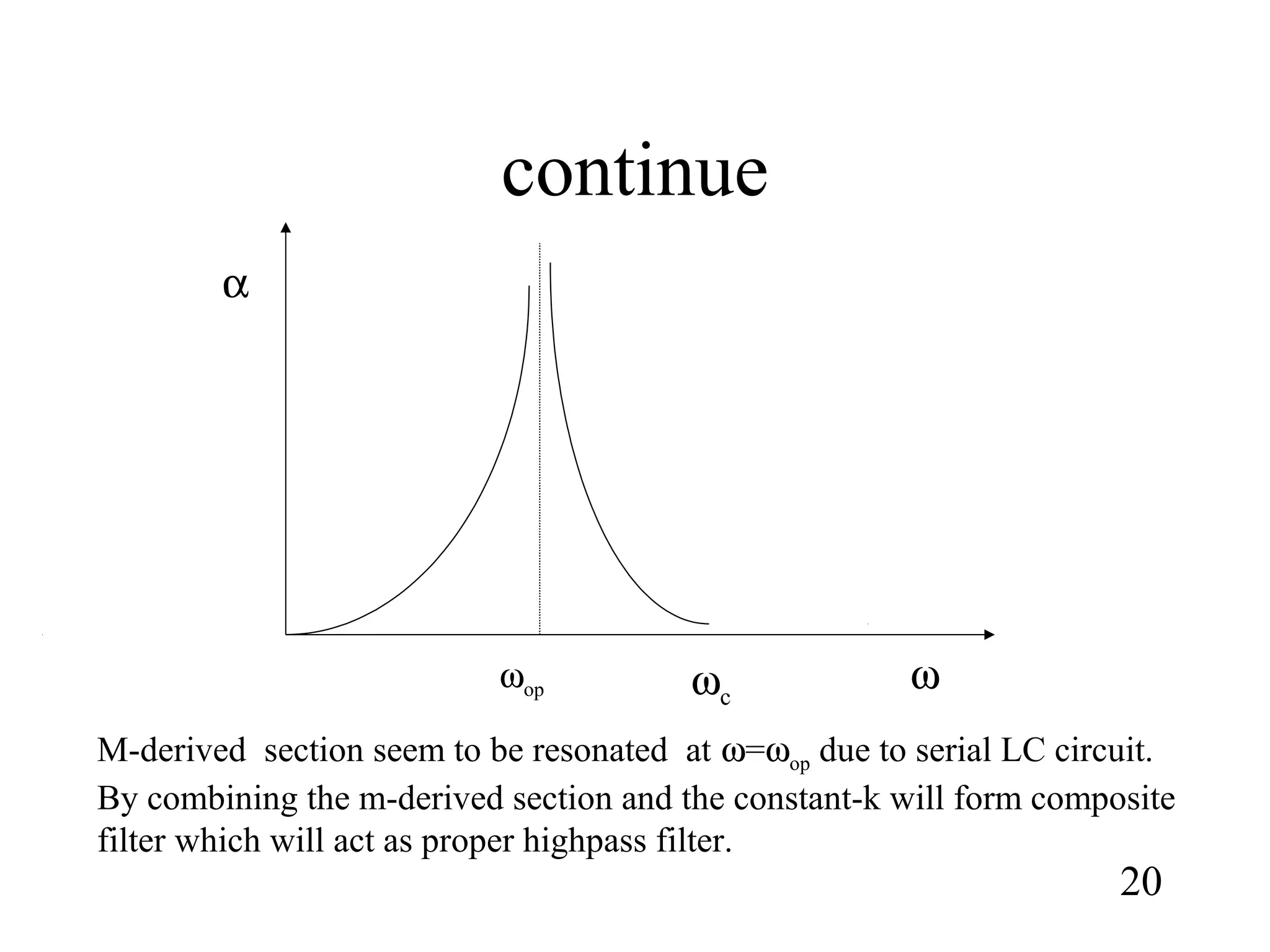
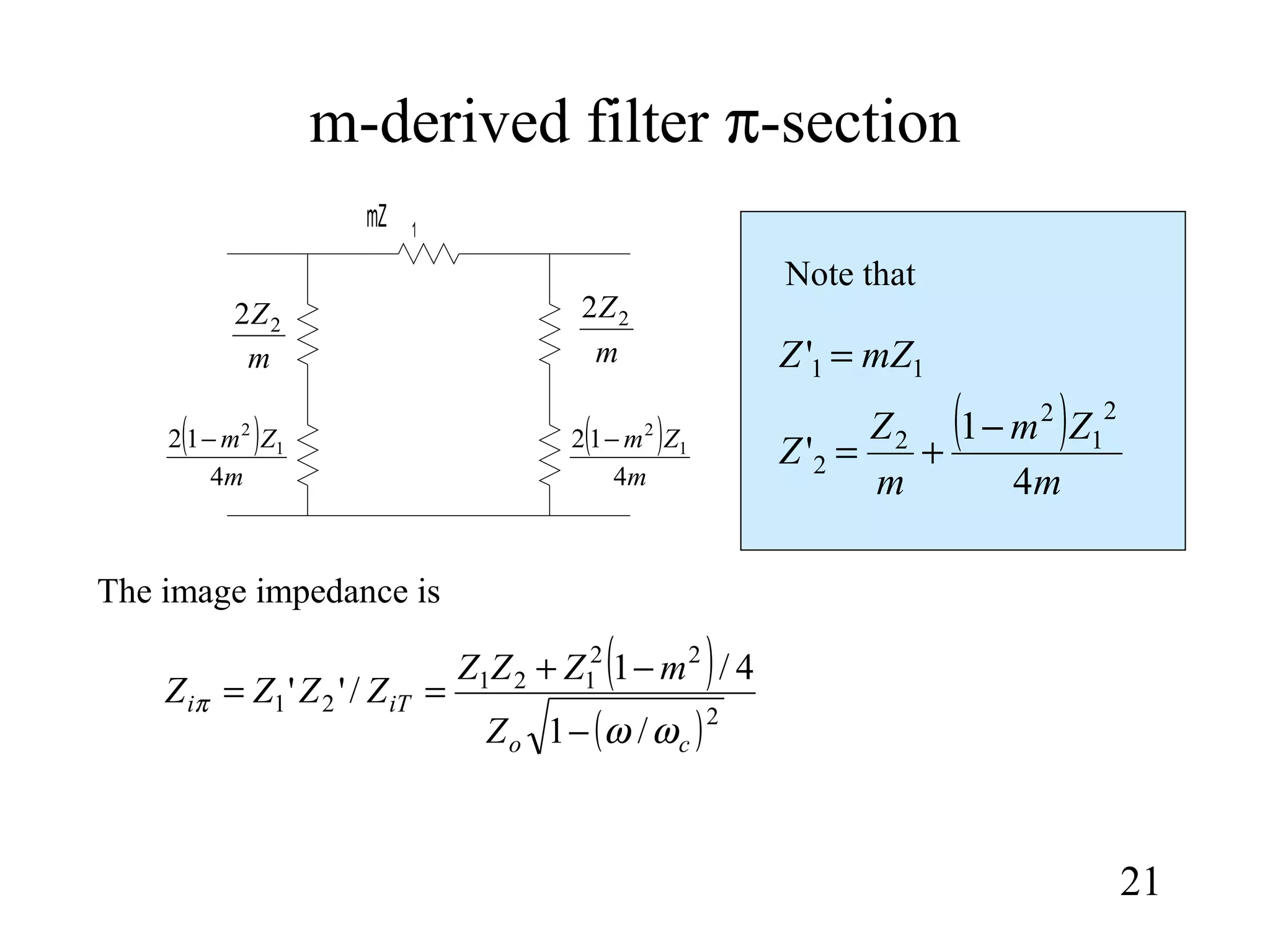
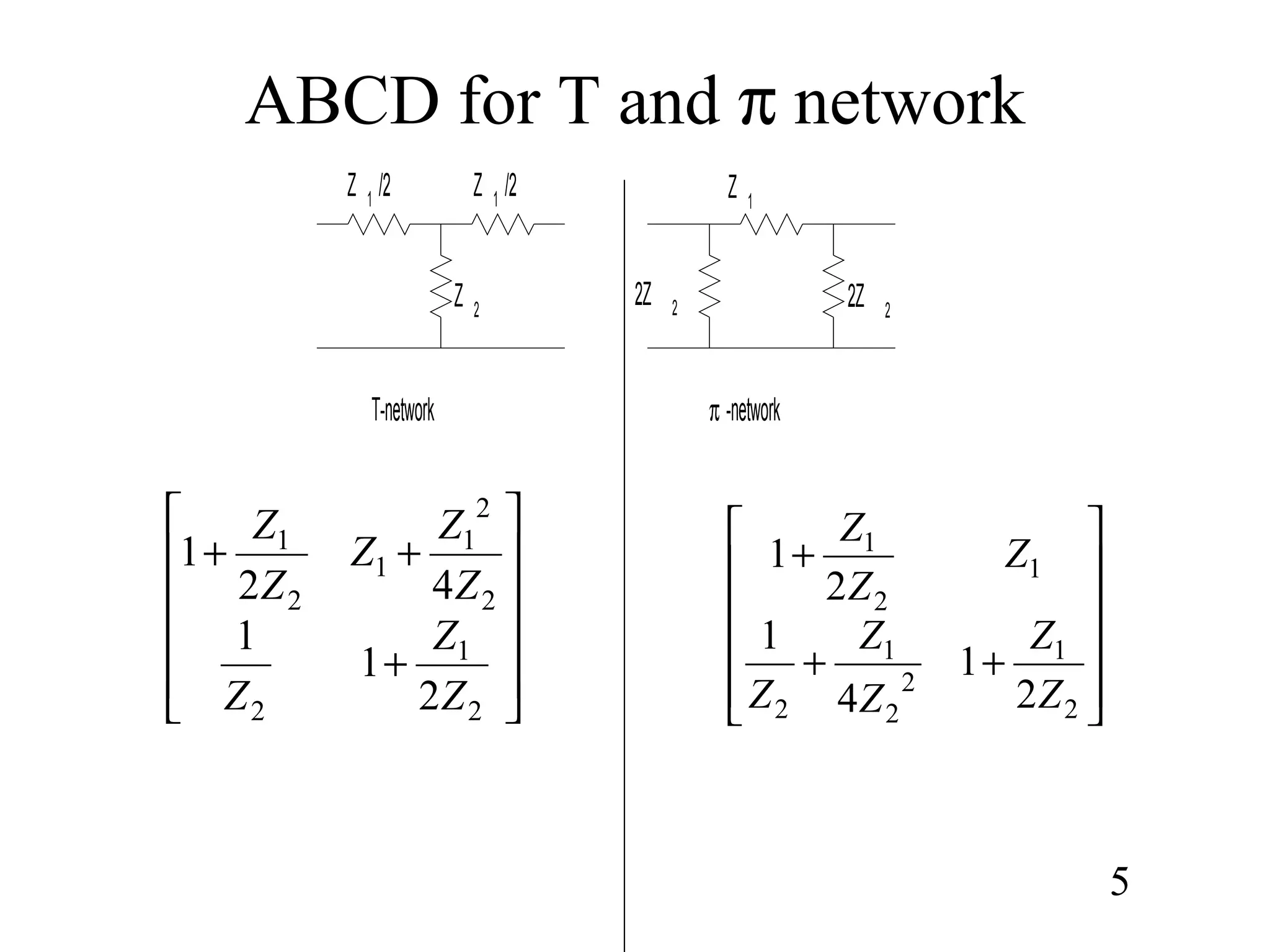
This document summarizes the design of microwave filters using composite, m-derived, T-network, and π-network sections. It describes: 1) How constant-k sections have very slow attenuation rates and non-constant image impedances. M-derived sections are introduced to address this by replacing component values to obtain the same image impedance as the constant-k section. 2) The propagation constant and image impedance equations for low-pass and high-pass T-network and π-network constant-k and m-derived sections. 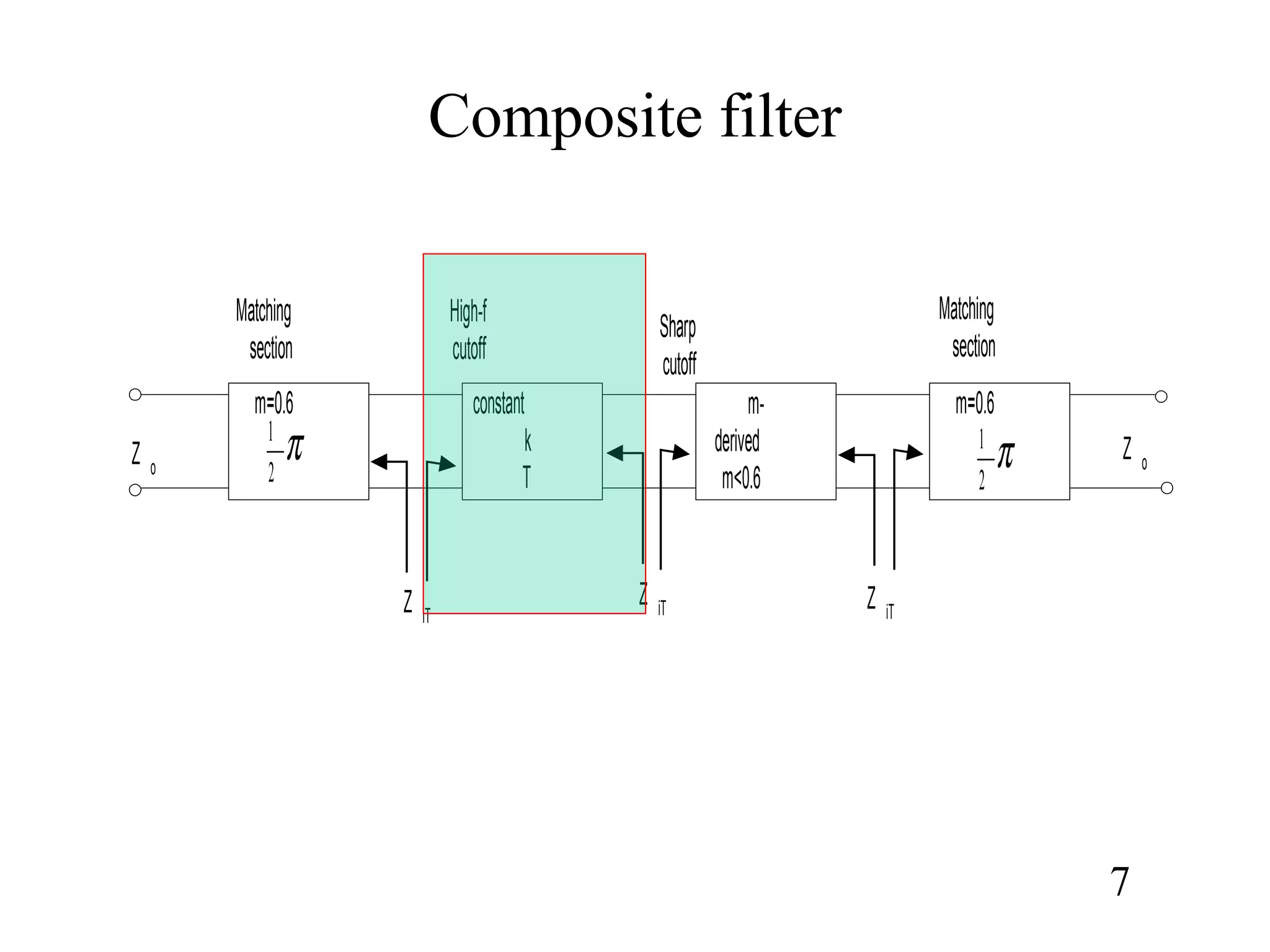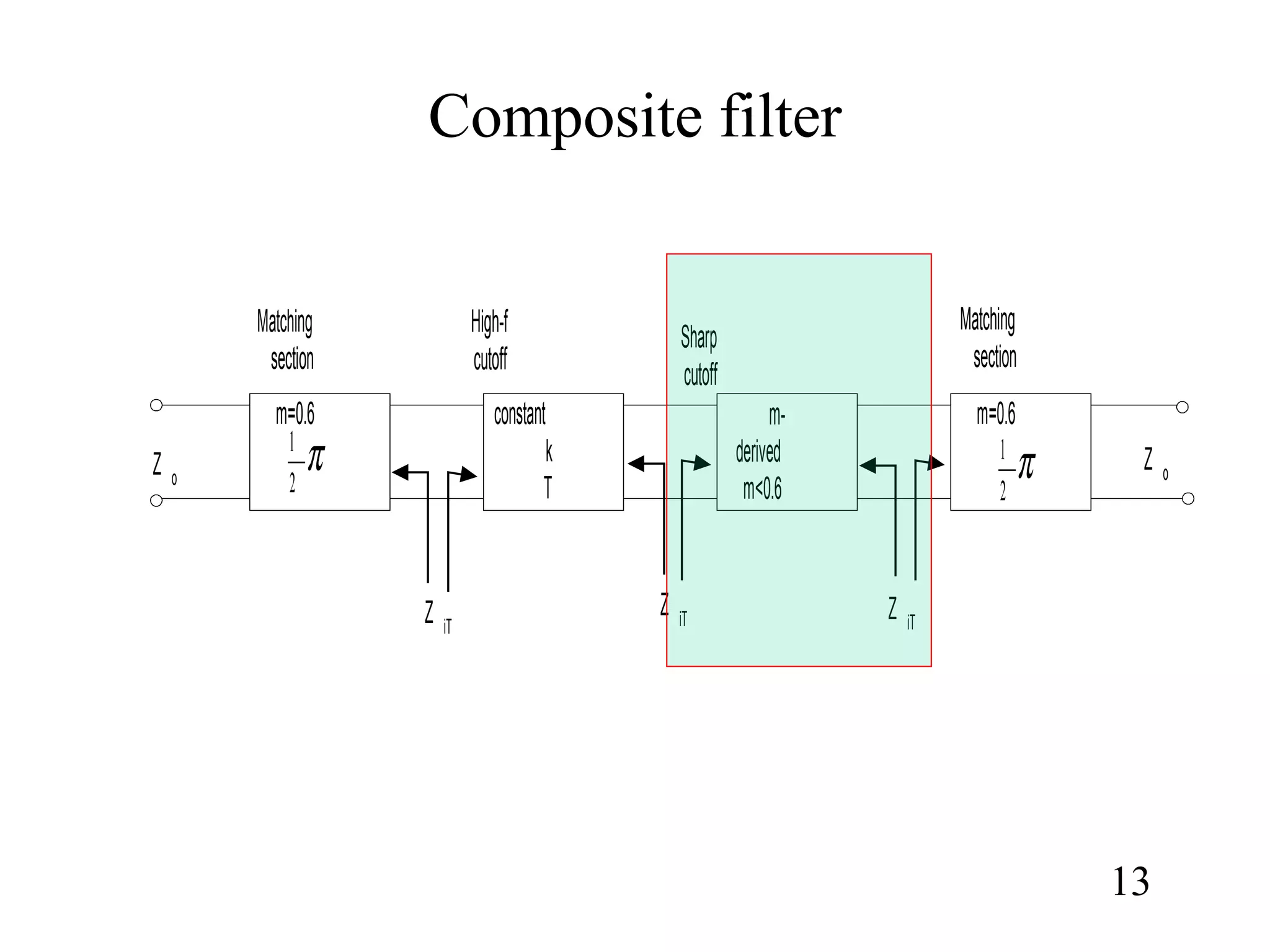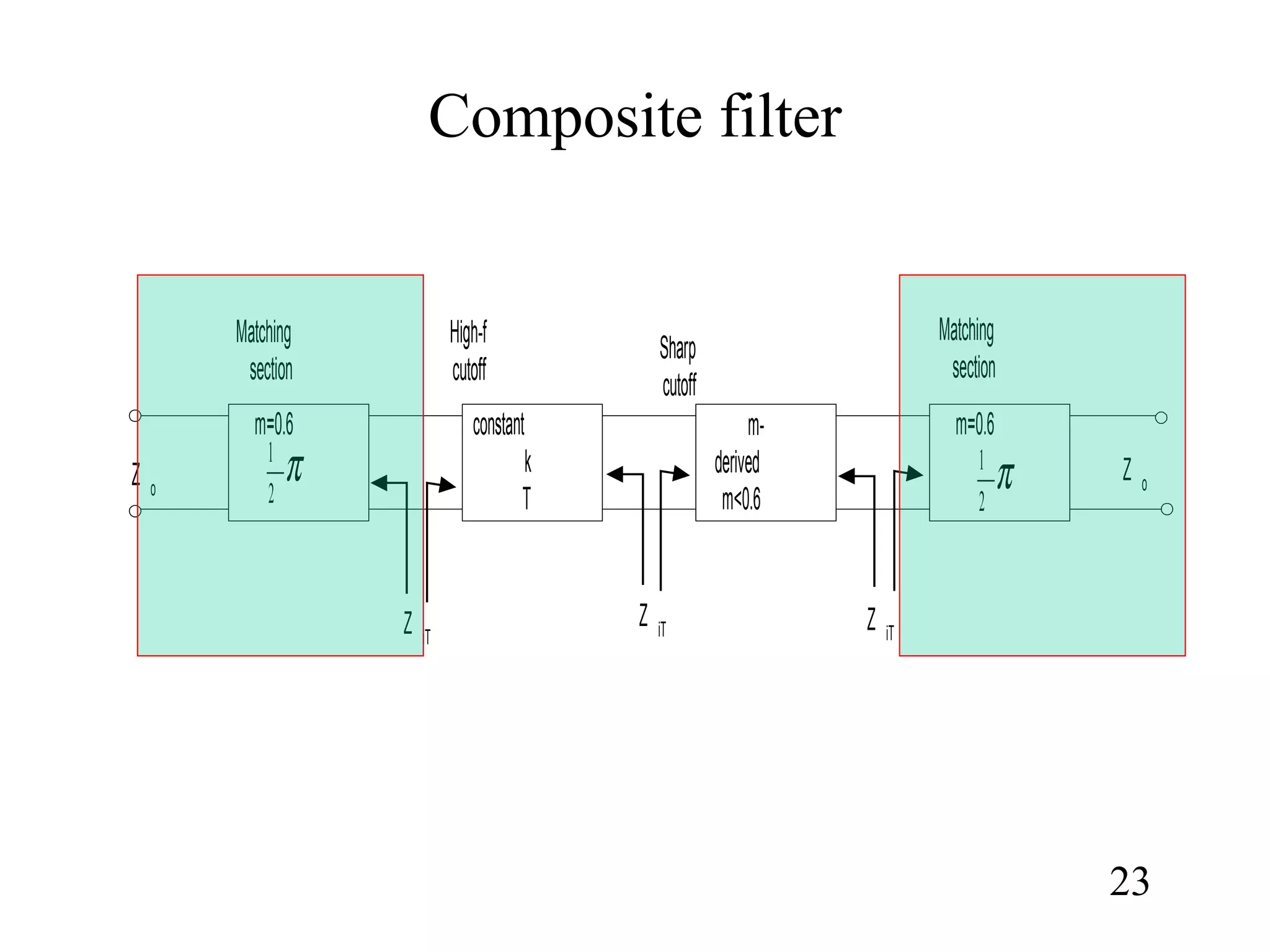3) Composite filters formed by combining m-derived and constant-k sections act as proper filters with rapid initial attenuation that does not reduce at higher

1. Microwave Filter Design
By
Professor Syed Idris Syed Hassan
Sch of Elect. & Electron Eng
Engineering Campus USM
Nibong Tebal 14300
SPS Penang

2. Contents
2
1. Composite filter
2. LC ladder filter
3. Microwave filter

3. Composite filter
3
m=0.6 m=0.6m-
derived
m<0.6
constant
k
T
π2
1
π2
1
Matching
section
Matching
section
High-f
cutoff
Sharp
cutoff
Z iT
Z iT Z iT
Z o
Z o
m<0.6 for m-derived section is to place the pole near the cutoff frequency(ωc)
oZZZZZ =+ 2121 '4/'1''
iTZZZZZ =+ 2121 '4/'1/''
For 1/2 π matching network , we choose the Z’1 and Z’2 of the circuit so that

4. Image method






DC
BA
Z i1 Z i2
I 1 I 2
+
V 1
-
+
V 2
-
Z in1 Z in2
221
221
DICVI
BIAVV
+=
+=
Let’s say we have image impedance for the network Zi1 and Zi2
Where
Zi1= input impedance at port 1 when port 2 is terminated with Zi2
Zi2= input impedance at port 2 when port 1 is terminated with Zi1
Then
4
@
Where Zi2= V2 / I2
and V1 = -Zi1 I1

5. ABCD for T and π network
5
Z 1 /2 Z 1 /2
Z 2
Z 1
2Z 2 2Z 2
T-network π -network












++
+
2
1
2
2
1
2
1
2
1
2
1
4
1
2
1
Z
Z
Z
Z
Z
Z
Z
Z












+
++
2
1
2
2
2
1
1
2
1
2
1
1
42
1
Z
Z
Z
Z
Z
Z
Z
Z

6. Image impedance in T and π network
6
Z 1 /2 Z 1 /2
Z 2
Z 1
2Z 2 2Z 2
T-network π -network
2121 4/1 ZZZZZiT +=
( ) ( )2
2
2
12121 4//2/1 ZZZZZZe +++=γ
iTi ZZZZZZZZ /4/1/ 212121 =+=π
( ) ( )2
2
2
12121 4//2/1 ZZZZZZe +++=γ
Image impedance Image impedance
Propagation constant Propagation constant
Substitute ABCD in terms of Z1 and Z2 Substitute ABCD in terms of Z1 and Z2

7. Composite filter
7
m=0.6 m=0.6m-
derived
m<0.6
constant
k
T
π2
1
π2
1
Matching
section
Matching
section
High-f
cutoff
Sharp
cutoff
Z iT
Z iT Z iT
Z o
Z o

8. Constant-k section for Low-pass filter
using T-network
8
L/2
C
L/2
4
14/1
2
2121
LC
C
L
ZZZZZiT
ω
−=+=
LjZ ω=1
CjZ ω/12 =
If we define a cutoff frequency
LC
c
2
=ω
And nominal characteristic impedance
C
L
Zo =
Then
c
oiT ZZ 2
2
1
ω
ω
−= Zi T= Zo when ω=0

9. continue
9
Propagation constant (from page 11), we have
( ) ( ) 1
22
14//2/1 2
2
2
2
2
2
2
12121 −+−=+++=
ccc
ZZZZZZe
ω
ω
ω
ω
ω
ωγ
Two regions can be considered
∀ω<ωc : passband of filter --> Zit become real and γ is imaginary (γ= jβ )
since ω2
/ωc
2
-1<1
∀ω>ωc : stopband of filter_--> Zit become imaginary and γ is real (γ= α )
since ω2
/ωc
2
-1<1
ωc
ω
Mag
ωcα,β
ω
π
β
α
passband stopband

10. Constant-k section for Low-pass filter
using π-network
10
LjZ ω=1
CjZ ω/12 =








−
=








−
==
2
2
2
2
2
21
11
/
c
o
c
o
o
iTi
Z
Z
Z
ZZZZ
ω
ω
ω
ω
π
( ) ( ) 1
22
14//2/1 2
2
2
2
2
2
2
12121 −+−=+++=
ccc
ZZZZZZe
ω
ω
ω
ω
ω
ωγ
Zi π= Zo when ω=0
Propagation constant is the same as T-network
C/2
L
C/2

11. Constant-k section for high-pass filter
using T-network
11
LCC
L
ZZZZZiT 22121
4
1
14/1
ω
−=+=
CjZ ω/11 =
LjZ ω=2
If we define a cutoff frequency
LC
c
2
1
=ω
And nominal characteristic impedance
C
L
Zo =
Then
2
2
1
ω
ωc
oiT ZZ −= Zi T= Zo when ω = ∞
2C
L
2C

12. Constant-k section for high-pass filter
using π-network
12
CjZ ω/11 =
LjZ ω=2








−
=








−
==
2
2
2
2
2
21
11
/
c
c
o
c
o
o
iTi
Z
Z
Z
ZZZZ
ω
ω
ω
ω
π
( ) ( ) 1
22
14//2/1 2
2
2
2
2
2
2
12121 −+−=+++=
ω
ω
ω
ω
ω
ωγ ccc
ZZZZZZe
Zi π= Zo when ω=
Propagation constant is the same for both T and π-network
∞
2L
C
2L

13. Composite filter
13
m=0.6 m=0.6m-
derived
m<0.6
constant
k
T
π2
1
π2
1
Matching
section
Matching
section
High-f
cutoff
Sharp
cutoff
Z iT
Z iT Z iT
Z o
Z o

14. m-derived filter T-section
14
Z 1 /2 Z 1 /2
Z 2
Z' 1
/2 Z' 1
/2
Z' 2
mZ 1
/2 mZ 1
/2
Z 2 /m
1
2
4
1
Z
m
m−
Constant-k section suffers from very slow attenuation rate and non-constant
image impedance . Thus we replace Z1 and Z2 to Z’1 and Z’2 respectively.
Let’s Z’1 = m Z1 and Z’2 to obtain the same ZiT as in constant-k section.
4
'
4
'
''
4
2
1
2
21
2
1
21
2
1
21
Zm
ZmZ
Z
ZZ
Z
ZZZiT +=+=+=
4
'
4
2
1
2
21
2
1
21
Zm
ZmZ
Z
ZZ +=+
Solving for Z’2, we have
( )
m
Zm
m
Z
Z
4
1
'
2
1
2
2
2
−
+=

15. Low -pass m-derived T-section
15
L
m
m
4
1 2
−
mC
mL/2mL/2
LjZ ω=1
CjZ ω/12 =
For constant-k
section
LmjZ ω=1'
( ) Lj
m
m
Cmj
Z ω
ω 4
11
'
2
2
−
+=and
( ) ( )2
2
2
12121 '4/''/''2/'1 ZZZZZZe +++=γ
( ) ( )
( )
( )( )22
2
2
2
1
/11
/2
4/1/1'
'
c
c
m
m
mmLjCmj
Lmj
Z
Z
ωω
ωω
ωω
ω
−−
−
=
−+
=
( )
( )( )22
2
2
1
/11
/1
'4
'
1
c
c
mZ
Z
ωω
ωω
−−
−
=+
Propagation constant
LC
c
2
1
=ωwhere

16. continue
16
( )
( )2
2
2
1
/1
/1
'4
'
1
op
c
Z
Z
ωω
ωω
−
−
=+( )
( )2
2
2
1
/1
/2
'
'
op
cm
Z
Z
ωω
ωω
−
−
=
If we restrict 0 < m < 1 and
2
1 m
c
op
−
=
ω
ω
Thus, both equation reduces to
( )
( )
( )
( )
( )
( ) 







−
−








−
−
+
−
−
+= 2
2
2
2
2
2
/1
/1
/1
/2
/1
/2
1
op
c
op
c
op
c mm
e
ωω
ωω
ωω
ωω
ωω
ωωγ
Then
When ω < ωc, eγ
is imaginary. Then the wave is propagated in the
network. When ωc<ω <ωop, eγ
is positive and the wave will be attenuated.
When ω = ωop, eγ
becomes infinity which implies infinity attenuation.
When ω>ωop, then eγ
become positif but decreasing.,which meant
decreasing in attenuation.

17. Comparison between m-derived section
and constant-k section
17
Typical attenuation
0
5
10
15
0 2 4ω c
attenuation
m-derived
const-k
composite
ωop
M-derived section attenuates rapidly but after ω>ωop , the attenuation
reduces back . By combining the m-derived section and the constant-k will
form so called composite filter.This is because the image impedances are
nonconstant.

18. High -pass m-derived T-section
18
2C/m
L/m
2C/m
C
m
m
2
1
4
−
CjmZ ω/'1 =
( )
Cmj
m
m
Lj
Z
ω
ω
4
1
'
2
2
−
+=
and
( ) ( )2
2
2
12121 '4/''/''2/'1 ZZZZZZe +++=γ
( ) ( )
( )
( )( )22
2
2
2
1
/11
/2
4/1/
/
'
'
ωω
ωω
ωω
ω
c
c
m
m
CmjmmLj
Cjm
Z
Z
−−
−
=
−+
=
( )
( )( )22
2
2
1
/11
/1
'4
'
1
ωω
ωω
c
c
mZ
Z
−−
−
=+
Propagation constant
LC
c
2
1
=ωwhere

19. continue
19
( )
( )2
2
2
1
/1
/1
'4
'
1
ωω
ωω
op
c
Z
Z
−
−
=+( )
( )2
2
2
1
/1
/2
'
'
ωω
ωω
op
c m
Z
Z
−
−
=
If we restrict 0 < m < 1 and cop m ωω 2
1−=
Thus, both equation reduces to
( )
( )
( )
( )
( )
( ) 







−
−








−
−
+
−
−
+= 2
2
2
2
2
2
/1
/1
/1
/2
/1
/2
1
ωω
ωω
ωω
ωω
ωω
ωωγ
op
c
op
c
op
c mm
e
Then
When ω < ωop , eγ
is positive. Then the wave is gradually attenuated in
the networ as function of frequency. When ω = ωop, eγ
becomes infinity
which implies infinity attenuation. When ωχ>ω >ωop, eγ
is becoming
negative and the wave will be propagted.
Thus ωop< ωc

20. continue
20
α
ωωop ωc
M-derived section seem to be resonated at ω=ωop due to serial LC circuit.
By combining the m-derived section and the constant-k will form composite
filter which will act as proper highpass filter.

21. m-derived filter π-section
21
mZ 1
m
Z22
m
Z22
( )
m
Zm
4
12 1
2
−( )
m
Zm
4
12 1
2
−
( )
( )2
22
121
21
/1
4/1
/''
co
iTi
Z
mZZZ
ZZZZ
ωω
π
−
−+
==
11' mZZ =
( )
m
Zm
m
Z
Z
4
1
'
2
1
2
2
2
−
+=
Note that
The image impedance is

22. Low -pass m-derived π-section
22
mL
2
mC
2
mC
( )
m
Lm
4
12 2
−( )
m
Lm
4
12 2
−
LjZ ω=1
CjZ ω/12 =
For constant-k
section
2
21 / oZCLZZ == ( )22222
1 /4 coZLZ ωωω −=−=
Then
and
Therefore, the image impedance reduces to
( )( )
( )
o
c
c
i Z
m
Z
2
22
/1
/11
ωω
ωω
π
−
−−
=
The best result for m is 0.6which give a good constant Ziπ . This type of
m-derived section can be used at input and output of the filter to provide
constant impedance matching to or from Zo .

23. Composite filter
23
m=0.6 m=0.6m-
derived
m<0.6
constant
k
T
π2
1
π2
1
Matching
section
Matching
section
High-f
cutoff
Sharp
cutoff
Z iT
Z iT Z iT
Z o
Z o

24. Matching between constant-k and m-derived
24
πiiT ZZ ≠The image impedance ZiT does not match Ziπ, I.e
The matching can be done by using half- π section as shown below and the
image impedance should be Zi1= ZiT and Zi2=Ziπ
Z' 1
/2
2Z' 2
Z i2
=Z iπZ i1
=Z iT












+
1
'2
1
2
'
'4
'
1
2
1
2
1
Z
Z
Z
Z
12121 '4/'1'' iiT ZZZZZZ =+=
22121 '4/'1/'' ii ZZZZZZ =+=π
It can be shown that
11' mZZ =
( )
m
Zm
m
Z
Z
4
1
'
2
1
2
2
2
−
+=
Note that

25. Example #1
25
Design a low-pass composite filter with cutoff frequency of 2GHz and
impedance of 75Ω . Place the infinite attenuation pole at 2.05GHz, and plot
the frequency response from 0 to 4GHz.
Solution
For high f- cutoff constant -k T - section
C
L/2 L/2
LC
c
2
=ω
C
L
Zo =
L
C
c
12
2






=
ω
2
oZ
L
C = 2
oCZL =or
C
L
c
12
2






=
ω
Rearrange for ωc and substituting, we have
nHZL co 94.11)1022/()752(/2 9
=×××== πω
pFZC co 122.2)10275/(2/2 9
=××== πω

26. continue
26
cop m ωω 2
1−=
( ) ( ) 2195.01005.2/1021/1
2992
=××−=−= opcm ωω
For m-derived T section sharp cutoff
nH
nHmL
31.1
2
94.112195.0
2
=
×
=
pFpFmC 4658.0122.22195.0 =×=
nHnHL
m
m
94.1294.11
2195.04
2195.01
4
1 22
=
×
−
=
−
L
m
m
4
1 2
−
mC
mL/2mL/2

27. continue
27
For matching section
mL/2
mC/2mC/2
( )
m
Lm
2
1 2
−( )
m
Lm
2
1 2
−
mL/2
Z iT
Z o
Z o
m=0.6
nH
nHmL
582.3
2
94.116.0
2
=
×
=
pF
pFmC
6365.0
2
122.26.0
2
=
×
=
nHnHL
m
m
368.694.11
6.02
6.01
2
1 22
=
×
−
=
−

28. continue
28
3.582nH 5.97nH 1.31nH
6.368nH
0.6365pF
2.122pF
12.94nH
0.4658pF
3.582nH
6.368nH
0.6365pF
1.31nH5.97nH
Canbeadded
together
Canbeadded
together
Canbeadded
together
A full circuit of the filter

29. Simplified circuit
12.94nH
9.552nH
6.368nH
7.28nH 4.892nH
0.6365pF 0.6365pF0.4658pF
2.122pF
6.368nH

30. continue
30
Freq response of low-pass filter
-60
-40
-20
0
0 1 2 3 4
Frequency (GHz)
S11
Pole due to
m=0.2195
section
Pole due to
m=0.6
section

31. N-section LC ladder circuit
(low-pass filter prototypes)
31
g o
=G o
g 1
g 2
g 3
g 4
g n+1
g o
=R o
g 1
g 2
g 3
g 4
g n+1
Prototype beginning with serial element
Prototype beginning with shunt element

32. Type of responses for n-section prototype filter
32
•Maximally flat or Butterworth
•Equal ripple or Chebyshev
•Elliptic function
•Linear phase
Maximally flat Equal ripple Elliptic Linear phase

33. Maximally flat or Butterworth filter
33
( )
12
2
1
−














+=
n
c
CH
ω
ω
ω
For low -pass power ratio response
( )



 −
=
n
k
gk
2
12
sin2
π
g0 = gn+1 = 1
( )
( )c
A
n
ωω /log2
110log
110
10/
10 −
= co
k
k
Z
g
C
ω
=
c
ko
k
gZ
L
ω
=
where
C=1 for -3dB cutoff point
n= order of filter
ωc= cutoff frequency
No of order (or no of elements)
Where A is the attenuation at ω1 point and ω1>ωc
Prototype elements
k= 1,2,3…….n
Series element
Shunt element
Series R=Zo
Shunt G=1/Zo

34. Example #2
34
Calculate the inductance and capacitance values for a maximally-flat low-
pass filter that has a 3dB bandwidth of 400MHz. The filter is to be
connected to 50 ohm source and load impedance.The filter must has a high
attenuation of 20 dB at 1 GHz.
( )
( )c
A
n
ωω /log2
110log
110
10/
10 −
=
( ) 1
32
12
sin21 =



×
−
=
π
g
g0 = g 3+1 = 1First , determine the number of elements
Solution
( )
( )
51.2
400/1000log2
110log
10
10/20
10
>
−
=
c
Thus choose an integer value , I.e n=3
Prototype values
( ) 2
32
122
sin22 =



×
−×
=
π
g
( ) 1
32
132
sin23 =



×
−×
=
π
g

35. continue
35
nH
gZ
LL
c
o
9.19
104002
150
6
1
13 =
×××
×
===
πω
pF
Z
g
C
co
9.15
10400250
2
6
2
2 =
××××
==
πω
15.9pF
19.9nH
50ohm
50ohm 19.9nH

36. or
36
nH
gZ
L
c
o
8.39
104002
250
6
2
2 =
×××
×
==
πω
pF
Z
g
CC
co
95.7
10400250
1
6
1
13 =
××××
===
πω
7.95pF
39.8nH
50ohm
50ohm
7.95pF

37. Equi-ripple filter
37
( )
1
2
1
−














+=
c
noCFH
ω
ω
ω
For low -pass power ratio response
110 10/
−= Lr
oF
where
Cn(x)=Chebyshev polinomial for n order
and argument of x
n= order of filter
ωc= cutoff frequency
Fo=constant related to passband ripple
Chebyshev polinomial
Where Lr is the ripple attenuation in pass-band
(x)(x)-CCx(x)C n-n-n 212=
x(x)C =1
cn ei)(C ωω == .11
1=(x)Co

38. Continue
38
Prototype elements












=
372.17
cothln
4
1
1
Lr
F
( )


=+
evennforF
oddnfor
gn
1
21
coth
1
ckk
kk
k
bb
aa
g
1
1
−
−
=
2
1
1
F
a
g =
where






=
n
F
F 1
2
2
sinh
( ) nk
n
k
ak ,....2,1
2
1
sin2 =





 −
=
π
nk
n
k
Fbk ,....2,1
2
sin22
2 =





+=
π
c
ko
k
gZ
L
ω
=
co
k
k
Z
g
C
ω
=
Series element
Shunt element

39. Example #3
39
Design a 3 section Chebyshev low-pass filter that has a ripple of 0.05dB
and cutoff frequency of 1 GHz.
From the formula given we have
g2= 1.1132
g1 = g3 = 0.8794
F1=1.4626 F2= 1.1371
a1=1.0 a2=2.0
b1=2.043
nHLL 7
102
8794.050
931 =
×
×
==
π
pFC 543.3
10250
1132.1
92 =
××
=
π
3.543pF
7nH
50ohm
50ohm 7nH

40. Transformation from low-pass to high-pass
40
•Series inductor Lk must be replaced by capacitor C’k
•Shunts capacitor Ck must be replaced by inductor L’k
ck
o
k
g
Z
L
ω
=
cko
k
gZ
C
ω
1
=
ω
ω
ω
ω c
c
−→
g o =R o
g 1
g 2
g 3
g 4
g n+1

41. Transformation from low-pass to band-pass
41
•Thus , series inductor Lk must be replaced by serial Lsk and Csk
o
k
sk
L
L
ωΩ
=
ko
sk
L
C
ω
Ω
=






−
Ω
→
ω
ω
ω
ω
ω
ω o
oc
1
where
oω
ωω 12 −
=Ω 21 ωωω =oand
sk
skk
o
k
o
k
o
o C
j
LjLjLjLjjX
'
'
111
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
−=
Ω
−
Ω
=





−
Ω
=
Now we consider the series inductor
kok gZL =
Impedance= series
normalized

42. continue
42
•Shunts capacitor Ck must be replaced by parallel Lpk and Cpk
ko
pk
C
L
ω
Ω
=
o
k
pk
C
C
ωΩ
=
pk
pkk
o
k
o
k
o
o
k
L
j
CjCjCjCjjB
'
'
111
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
−=
Ω
−
Ω
=





−
Ω
=
Now we consider the shunt capacitor
o
k
k
Z
g
C =
Admittance= parallel

43. Transformation from low-pass to band-stop
43
•Thus , series inductor Lk must be replaced by parallel Lpk and Cskp
o
k
pk
L
L
ω
Ω
=
ko
pk
L
C
Ω
=
ω
1
1
1
−






−
Ω
→
ω
ω
ω
ω
ω
ω o
oc
where
oω
ωω 12 −
=Ω 21 ωωω =oand
pk
pk
k
o
ko
o
okk L
j
Cj
L
j
L
j
L
j
X
j
'
'
1111
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
−=
Ω
−
Ω
=





−
Ω
=
Now we consider the series inductor --convert to admittance
kok gZL =
admittance = parallel

44. Continue
44
•Shunts capacitor Ck must be replaced by parallel Lpk and Cpk
ko
sk
C
L
ωΩ
=
1
o
k
pk
C
C
ω
Ω
=
sk
sk
k
o
ko
o
okk C
j
Lj
C
j
C
j
C
j
B
j
'
'
1111
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
−=
Ω
−
Ω
=





−
Ω
=
Now we consider the shunt capacitor --> convert to impedance
o
k
k
Z
g
C =

45. Example #4
45
Design a band-pass filter having a 0.5 dB ripple response, with N=3. The
center frequency is 1GHz, the bandwidth is 10%, and the impedance is 50Ω.
Solution
From table 8.4 Pozar pg 452.
go=1 , g1=1.5963, g2=1.0967, g3= 1.5963, g4= 1.000
Let’s first and third elements are equivalent to series inductance and g1=g3, thus
nH
gZ
LL
o
o
ss 127
1021.0
5963.150
9
1
31 =
××
×
=
Ω
==
πω
pF
gZ
CC
oo
ss 199.0
5963.150102
1.0
9
1
31 =
×××
=
Ω
==
πω
kok gZL =

46. continue
46
Second element is equivalent to parallel capacitance, thus
nH
g
Z
L
o
o
p 726.0
0967.1102
501.0
9
2
2 =
××
×
=
Ω
=
πω
pF
Z
g
C
oo
p 91.34
1021.050
0967.1
9
2
2 =
×××
=
Ω
=
πω
o
k
k
Z
g
C =
50 Ω 127nH 0.199pF
0.726nH 34.91pF
127nH 0.199pF
50 Ω

47. Implementation in microstripline
47
Equivalent circuit
A short transmission line can be equated to T and π circuit of lumped
circuit. Thus from ABCD parameter( refer to Fooks and Zakareviius
‘Microwave Engineering using microstrip circuits” pg 31-34), we have
jω L=jZ o sin( β d)
jω C/2=jY o ta n( β d)/2 jω C/2=jY o ta n( β d/2)
jω L/2=jZ o tan( β d/2)jω L/2=jZ o ta n( β d/2)
jω C=jY o
si n( β d)
Model for series inductor
with fringing capacitors
Model for shunt capacitor
with fringing inductors

48. 48
d
Z o
L
Z oL
Z o






=
d
oC
fC
dZ
L
λ
π
ω
tan





=
doL
fL
d
Z
C
λ
π
ω
tan
1
π-model with C as fringing
capacitance
Τ-model with L as fringing
inductance
ZoL should be high impedance
ZoC should be low impedance
d
Z o
Z oC
C Z o






= −
oL
d
Z
L
d
ω
π
λ 1
sin
2
( )oC
d
CZd ω
π
λ 1
sin
2
−
=

49. Example #5
49
From example #3, we have the solution for low-pass Chebyshev of ripple
0.5dB at 1GHz, Design a filter using in microstrip on FR4 (εr=4.5 h=1.5mm)
nHLL 731 == pFC 543.32 =
Let’s choose ZoL=100Ω and ZoC =20 Ω.
mm
Z
L
d
oL
d
25.10
100
107102
sin
2
1414.0
sin
2
99
11
3,1 =






 ×××
=





=
−
−− π
π
ω
π
λ
cm
f
c
r
d 14.14
5.410
103
9
8
=
×
==
ε
λ
pF
d
Z
C
doL
fL 369.0
1414.0
01025.0
tan
102100
1
tan
1
9
=




 ×
××
=





=
λ
π
πλ
π
ω
Note: For more accurate
calculate for difference Zo

50. continue
50
( ) ( ) mmCZd oC
d
38.102010543.3102sin
2
1414.0
sin
2
12911
2 =××××== −−−
π
π
ω
π
λ
nH
dZ
L
d
oC
fC 75.0
1414.0
01038.
tan
102
20
tan 9
=




 ×
×
=





=
λ
π
πλ
π
ω
pFC 543.32 =
The new values for L1=L3= 7nH-0.75nH= 6.25nH and C2=3.543pF-0.369pF=3.174pF
Thus the corrected value for d1,d2 and d3 are
mmd 08.9
100
1025.6102
sin
2
1414.0 99
1
3,1 =






 ×××
=
−
− π
π
( ) mmd 22.9201017.3102sin
2
1414.0 1291
2 =××××= −−
π
π
More may be needed to obtain sufficiently stable solutions

51. 51
mmmmh
Z
w
roL
31.05.157.1
5.4100
377
57.1
377
100 =





−=








−=
ε
mmmmh
Z
w
roL
97.105.157.1
5.420
377
57.1
377
20 =





−=








−=
ε






−
=
57.1
377
h
w
Z
r
o
ε
Now we calculate the microstrip width using this formula
(approximation)
mmmmh
Z
w
roL
97.25.157.1
5.450
377
57.1
377
50 =





−=








−=
ε
10.97mm
2.97mm
0.31mm
9.08mm
9.22mm
9.08mm
2.97mm
0.31mm

52. Implementation using stub
52
Richard’s transformation
βξ tanjLLjjXL == βξ tanjCCjjBc ==
At cutoff unity frequency,we have ξ=1. Then
1tan =β
8
λ
=
L
C
jX L
jB c
λ /8
S.C
O.C
Z o =L
Z o =1/C
jX L
jB c
λ /8
The length of the stub will be
the same with length equal
to λ/8. The Zo will be
difference with short circuit
for L and open circuit for
C.These lines are called
commensurate lines.

53. Kuroda identity
53
It is difficult to implement a series stub in microstripline.
Using Kuroda identity, we would be able to transform S.C
series stub to O.C shunt stub
d
d d d
S.Cseries
stub
O.Cshunt
stub
Z 1
Z 2
/n 2
n 2
=1+Z 2 /Z 1
Z 1 /n 2
Z 2
d=λ/8

54. Example #6
54
Design a low-pass filter for fabrication using micro strip lines .The
specification: cutoff frequency of 4GHz , third order, impedance 50 Ω, and a
3 dB equal-ripple characteristic.
Protype Chebyshev low-pass filter element values are
g1=g3= 3.3487 = L1= L3 , g2 = 0.7117 = C2 , g4=1=RL
1
1 3.3487
0.7117
3.3487
Using Richard’s transform we have
ZoL= L=3.3487 Zoc=1/ C=1/0.7117=1.405and
1
λ/ 8
1
λ/ 8
λ/ 8
λ/ 8
λ/ 8
Z oc =1.405
Z oL =3.3487Z oL =3.3487
Zo
Zo

55. Using Kuroda identity to convert S.C series stub to O.C shunt stub.
299.1
3487.3
1
11
1
22
=+=+=
Z
Z
n
3487.3
1
1
2
=
Z
Z
3487.3/ 2
1 == oLZnZ 1/ 2
2 == oZnZ
thus
We have
and
Substitute again, we have
35.43487.3299.12
1 =×== oLZnZ 299.1299.112
2 =×== nZZ oand
55
d d d
S.Cseries
stub
O.Cshunt
stub
Z 1
Z 2 /n 2
=Z o
n 2 =1+Z 2
/Z 1
Z 1
/n 2 =Z oL
Z 2

56. 50 Ω
217.5 Ω
64.9 Ω 70.3 Ω
λ /8
64.9 Ωλ /8
λ /8
217.5 Ω
50 Ω
56
λ /8
λ /8
λ /8
λ /8
λ /8
Z o =50 Ω
Z 2 =4.35x50
=217.5 Ω
Z 1
=1.299x50
=64.9 Ω
Zoc=1.405x50
=70.3 Ω
Z L =50 Ω
Z 1 =1.299x50
=64.9 Ω
Z 2 =4.35x50
=217.5 Ω

57. Band-pass filter from λ/2 parallel coupled lines
57
Input
λ /2resonator
λ /2resonator
Output
J' 0 1
+ π /2
rad
J' 23
+ π /2
rad
J' 12
+ π /2
rad
λ /4 λ /4λ /4
Microstrip
layout
Equivalent
admittance
inverter
Equivalent
LC resonator

58. Required admittance inverter parameters
58
2
1
10
01
2
'





 Ω
=
gg
J
π
1,...2,1
1
2
'
1
1, −=×
Ω
=
+
+ nkfor
gg
J
kk
kk
π
tionsofnon
gg
J
nn
nn sec.
2
'
2
1
1
1, =





 Ω
=
+
+
π
oω
ωω 12 −
=Ω
The normalized admittance inverter is given by
[ ]2
1,1,1, ''1, +++ ++= kkkkokkoe JJZZ
[ ]2
1,1,1,, ''1 +++ +−= kkkkokkoo JJZZ
okkkk ZJJ 1,1,' ++ =where
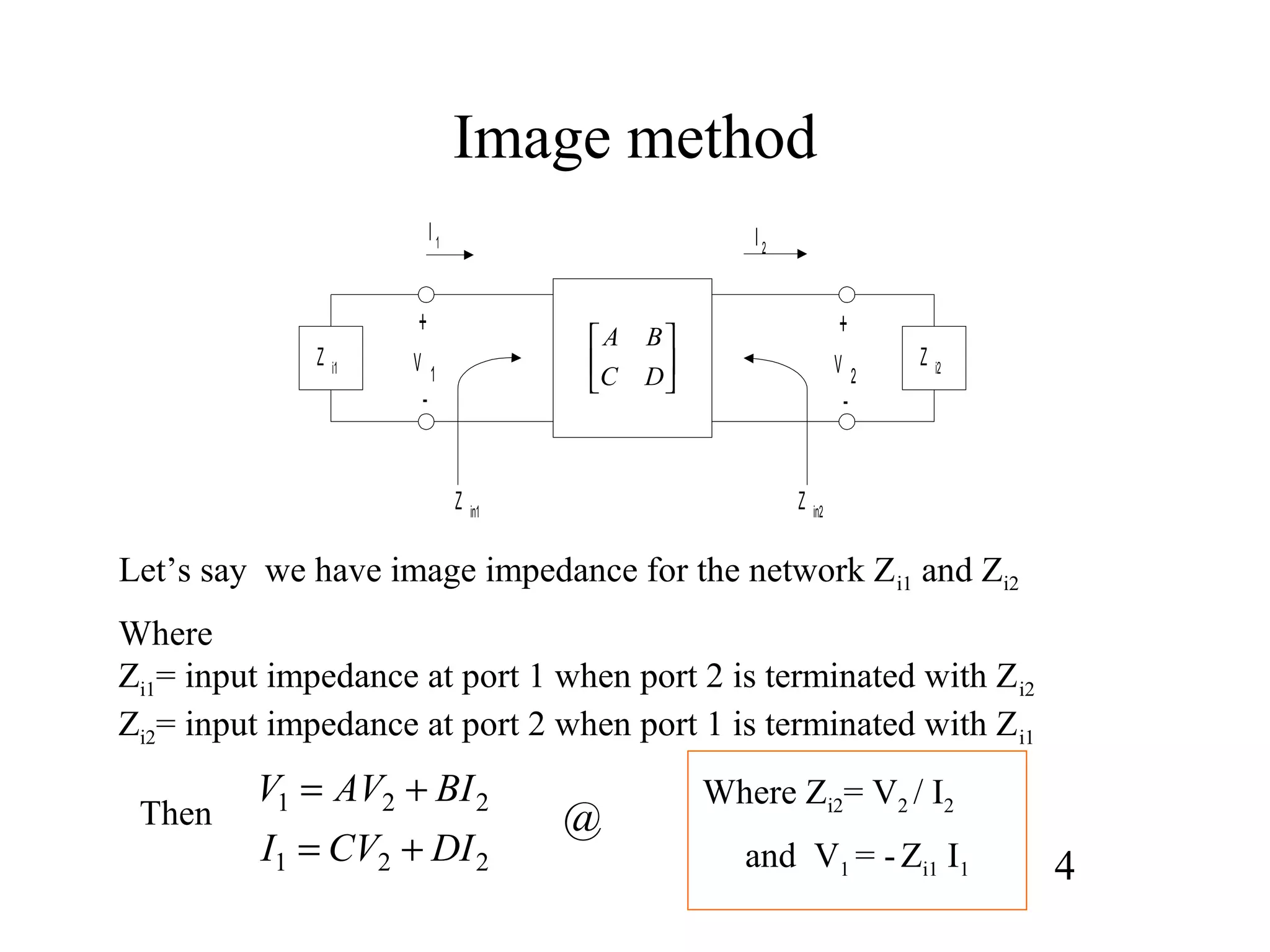
where A
B
C
D
E

59. Example #7
59
Design a coupled line bandpass filter with n=3 and a 0.5dB equi-ripple
response on substrate er=10 and h=1mm. The center frequency is 2 GHz, the
bandwidth is 10% and Zo=50Ω.
We have g0=1 , g1=1.5963, g2=1.0967, g3=1.5963, g4= 1 and Ω=0.1
3137.0
5963.112
1.0
2
'
2
1
2
1
10
01 =






××
×
=





 Ω
=
ππ
gg
J
[ ] Ω=++== 61.703137.03137.0150,, 2
4,31,0 oeoe ZZ
[ ] Ω=+−== 24.393137.03137.0150 2
4,3,1,0, oooo ZZ
3137.0
15963.12
1.0
2
'
2
1
2
1
43
4,3 =






××
×
=





 Ω
=
ππ
gg
J
A
C
D
E

60. 60
1187.0
0967.15963.1
1
2
1.01
2
'
21
2,1 =
×
×
×
=×
Ω
=
ππ
gg
J
1187.0
5963.10967.1
1
2
1.01
2
'
32
3,2 =
×
×
×
=×
Ω
=
ππ
gg
JB
B
[ ] Ω=++== 64.561187.01187.0150,, 2
3,22,1 oeoe ZZ
[ ] Ω=+−== 77.441187.01187.0150 2
3,2,2,1, oooo ZZ
D
E
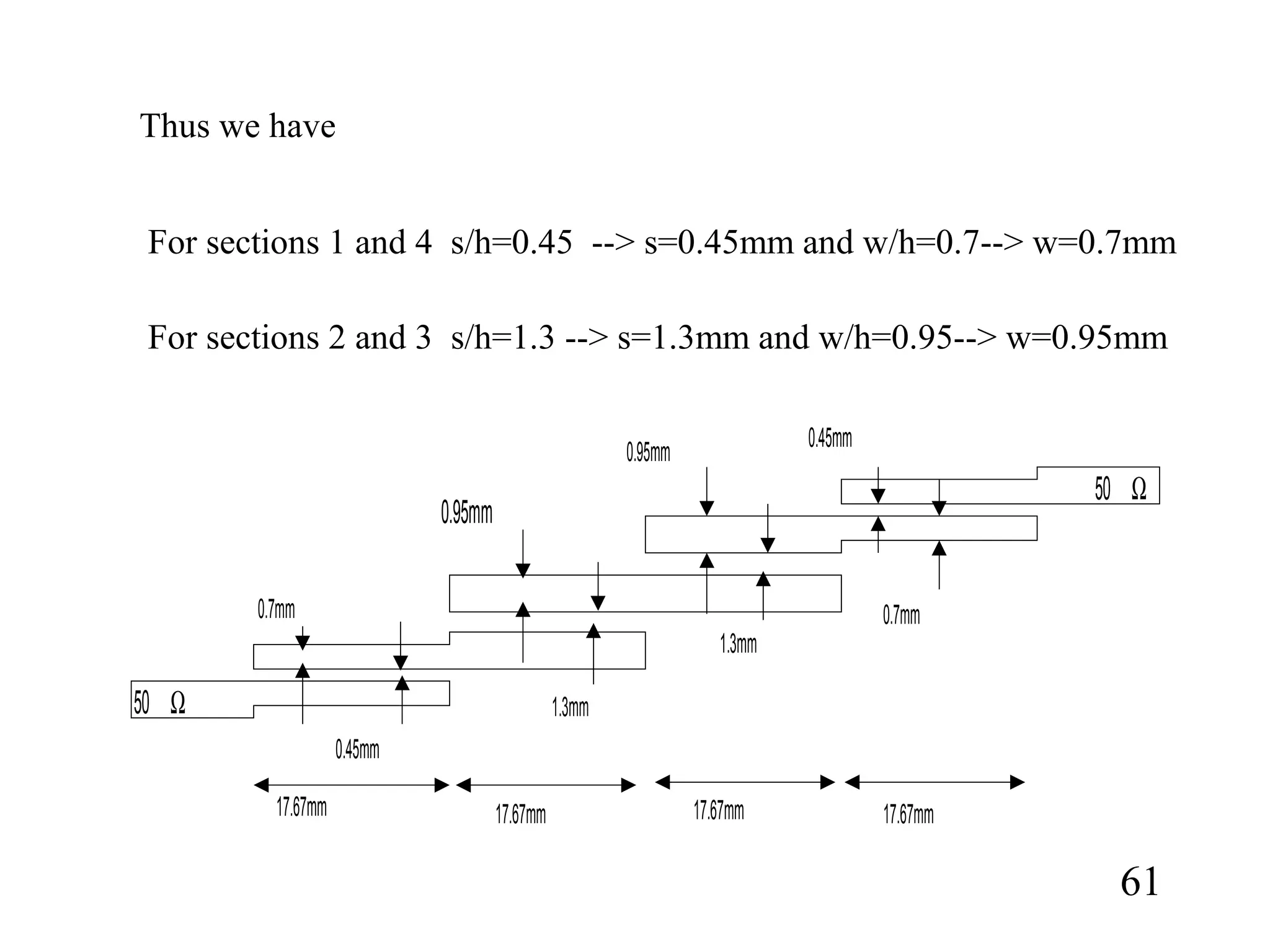
Using the graph Fig 7.30 in Pozar pg388 we would be able to determine the
required s/h and w/h of microstripline with εr=10. For others use other means.
m
f r
r 01767.0
101024
103
2
103
4/ 9
88
=
××
×
=
×
=
ε
λThe required resonator

61. 61
Thus we have
For sections 1 and 4 s/h=0.45 --> s=0.45mm and w/h=0.7--> w=0.7mm
For sections 2 and 3 s/h=1.3 --> s=1.3mm and w/h=0.95--> w=0.95mm
50 Ω
50 Ω
0.7mm
0.45mm
0.95mm
1.3mm
0.95mm
1.3mm
0.45mm
0.7mm
17.67mm 17.67mm 17.67mm 17.67mm

62. Band-pass and band-stop filter using quarter-wave stubs
62
n
o
on
g
Z
Z
4
Ω
=
π
n
o
on
g
Z
Z
Ω
=
π
4
Band-pass
Band-stop
....
Z 01
Z 02 Z on-1
Z on
Z o
Z oZ oZ o
Z o
λ /4
λ /4λ /4λ /4λ /4
λ /4
....
Z 01
Z 02
Z on-1 Z on
Z o
Z oZ oZ o
Z o
λ /4
λ /4λ /4λ /4λ /4
λ /4

63. Example #8
63
Design a band-stop filter using three quarter-wave open-circuit stubs . The
center frequency is 2GHz , the bandwidth is 15%, and the impedance is 50W.
Use an equi-ripple response, with a 0.5dB ripple level.
We have g0=1 , g1=1.5963, g2=1.0967, g3=1.5963, g4= 1 and Ω=0.1
n
o
on
g
Z
Znote
Ω
=
π
4
:
Ω=
××
×
== 9.265
5963.115.0
504
031
π
ZZo
Ω=
××
×
= 387
0967.115.0
504
2
π
oZ
50 Ω
λ /4
265.9Ω
387Ω
265.9Ω
λ /4
λ/4
λ/4
λ/4
Note that: It is difficult to
impliment on microstripline
or stripline for characteristic
> 150Ω.

64. Capacitive coupled resonator band-pass filter
64
Z o Z oZ oZ o
....
B 2B 1
θ 2θ 1
B n+1
Z o
θ n
2
1
10
01
2
'





 Ω
=
gg
J
π
1,...2,1
1
2
'
1
1, −=×
Ω
=
+
+ nkfor
gg
J
kk
kk
π
tionsofnon
gg
J
nn
nn sec.
2
'
2
1
1
1, =





 Ω
=
+
+
π
oω
ωω 12 −
=Ωwhere
( )2
1 io
i
i
JZ
J
B
−
=
( )[ ] ( )[ ]1
11
2tan
2
1
2tan
2
1
+
−−
++= ioioi BZBZπθ
i=1,2,3….n

65. Example #9
65
Design a band-pass filter using capacitive coupled resonators , with a
0.5dB equal-ripple pass-band characteristic . The center frequency is 2GHz,
the bandwidth is 10%, and the impedance 50W. At least 20dB attenuation
is required at 2.2GHz.
First , determine the order of filter, thus calculate
91.1
2.2
2
2
2.2
1.0
11
=





−=





−
Ω ω
ω
ω
ω o
o
91.0191.11 =−=−
cω
ω
From Pozar ,Fig 8.27 pg 453 , we have N=3
prototype
n gn ZoJn Bn Cn θn
1 1.5963 0.3137 6.96x10-3
0.554pF 155.8o
2 1.0967 0.1187 2.41x10-3
0.192pF 166.5o
3 1.0967 0.1187 2.41x10-3
0.192pF 155.8o
4 1.0000 0.3137 6.96x10-3
0.554pF -

66. Other shapes of microstripline filter
66
Rectangular resonator filter
U type filter
λ /4
In
Out
λ /4
In Out
Interdigital filterλ /2
in
out

67. Wiggly coupled line
ϕ 1
ϕ 2
67
ϕ1= π/2
ϕ2= π/4
The design is similar to conventional edge coupled line but the layout is
modified to reduce space.
ϕ 1
Modified Wiggly coupled line to improve 2nd and 3rd harmonic rejection. λ/8
stubs are added.