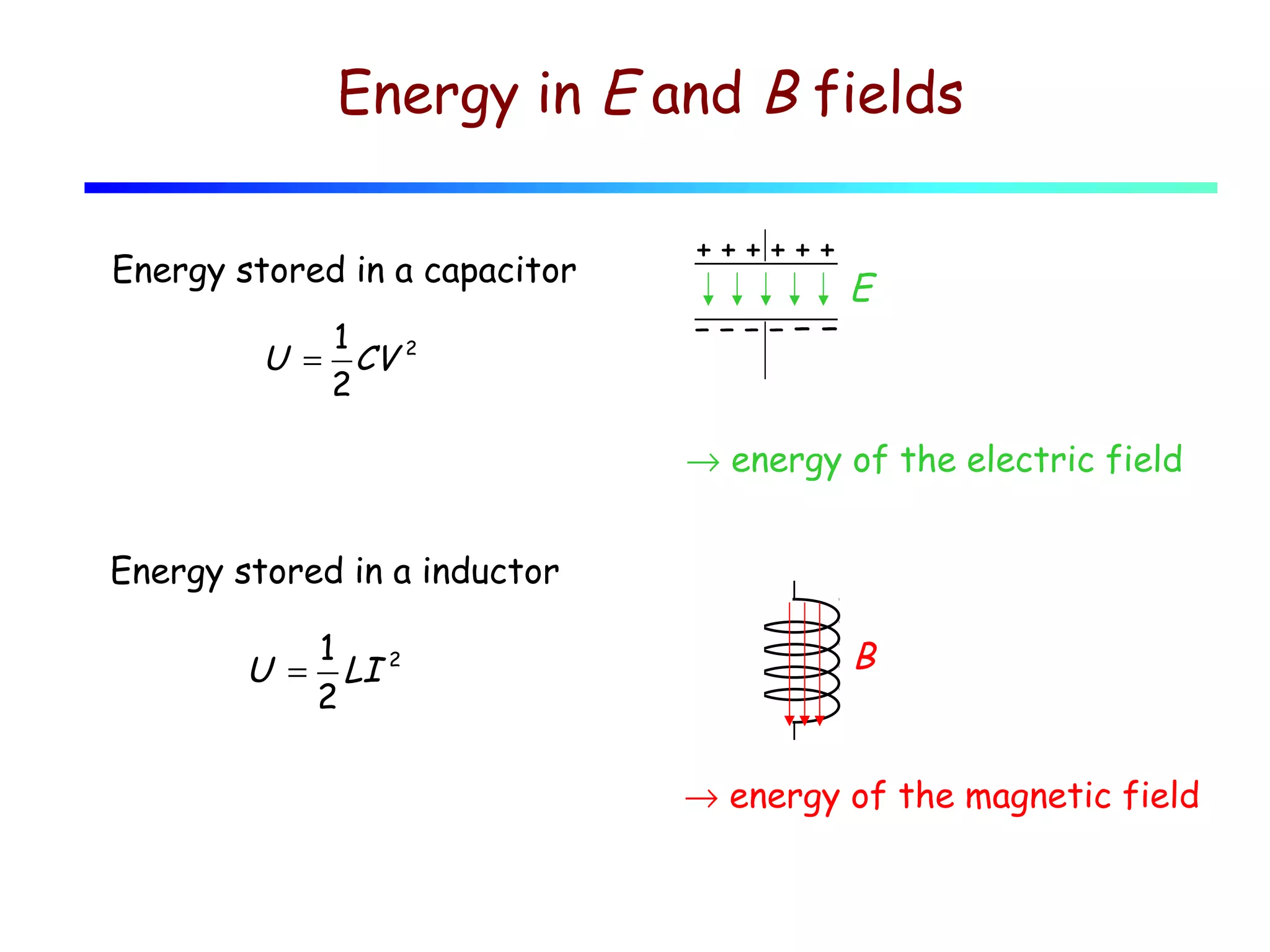
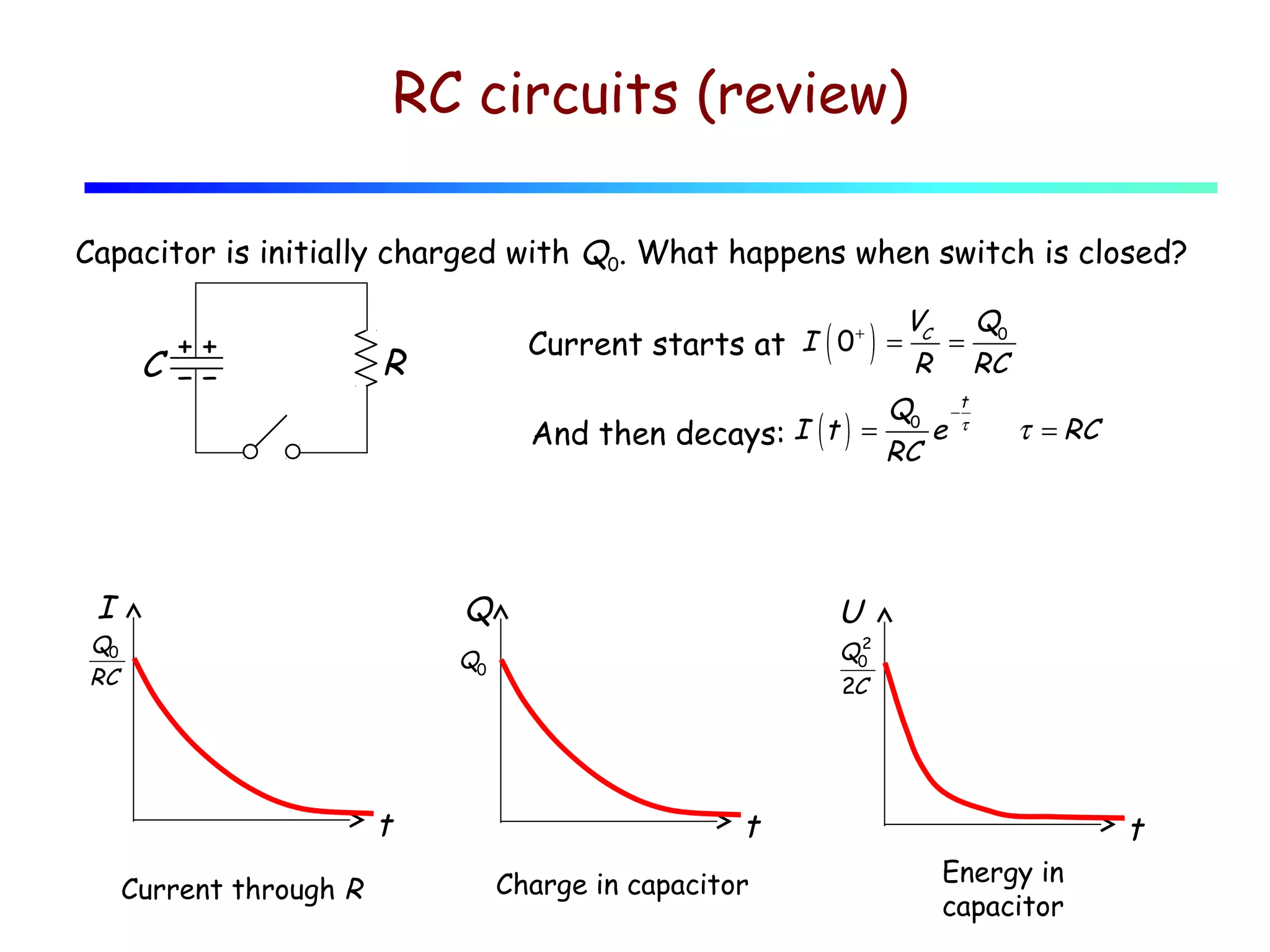
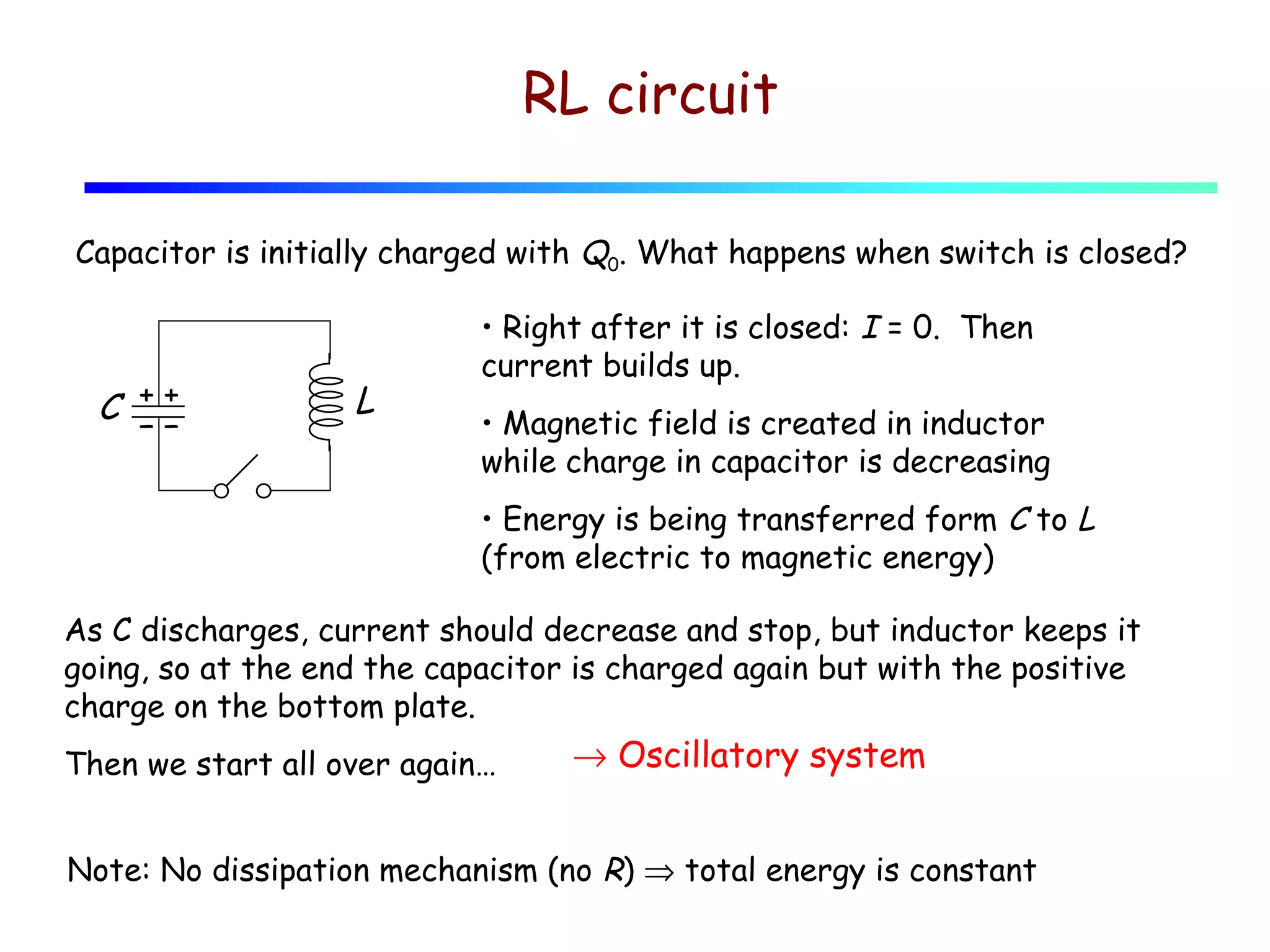
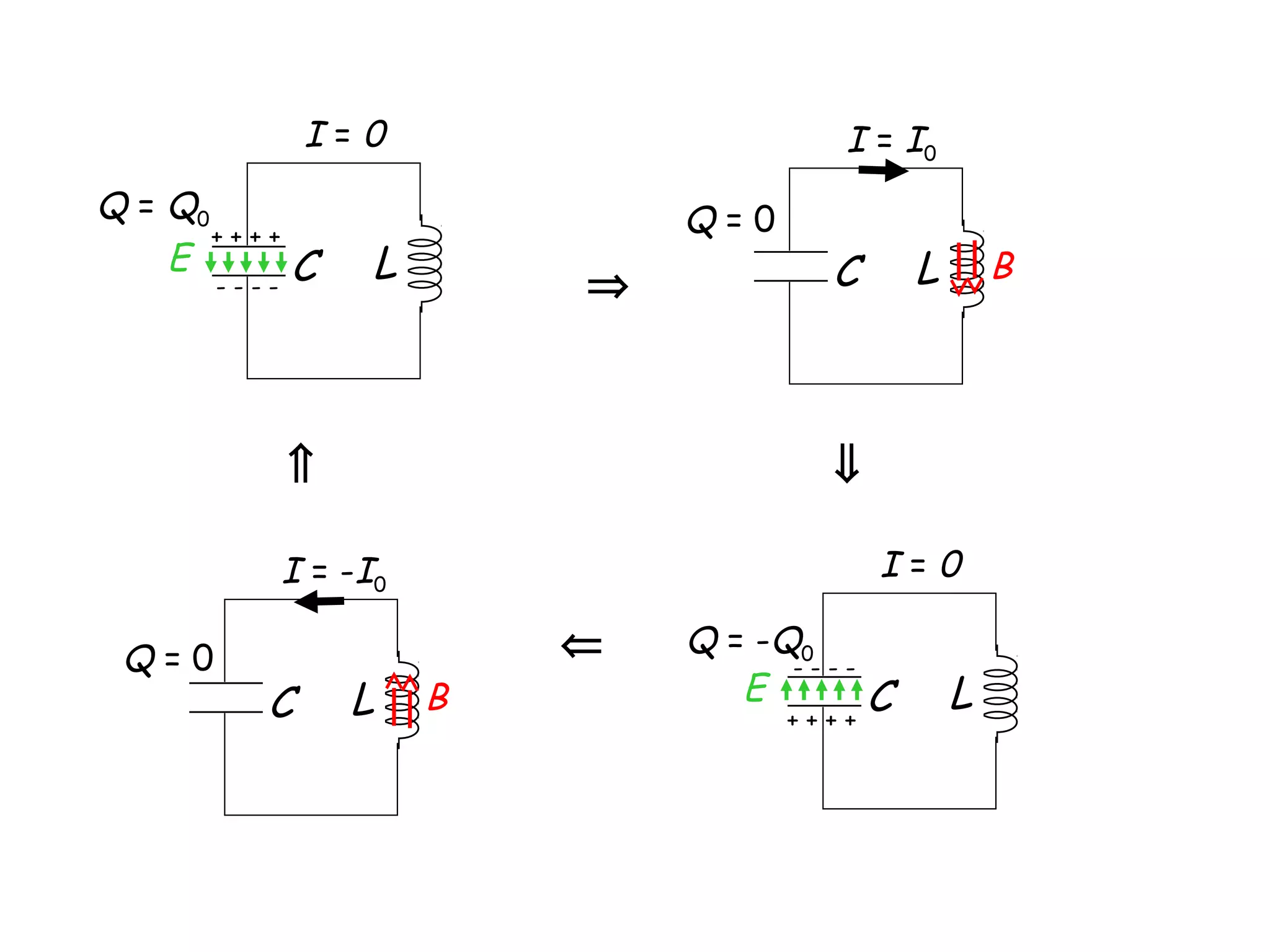
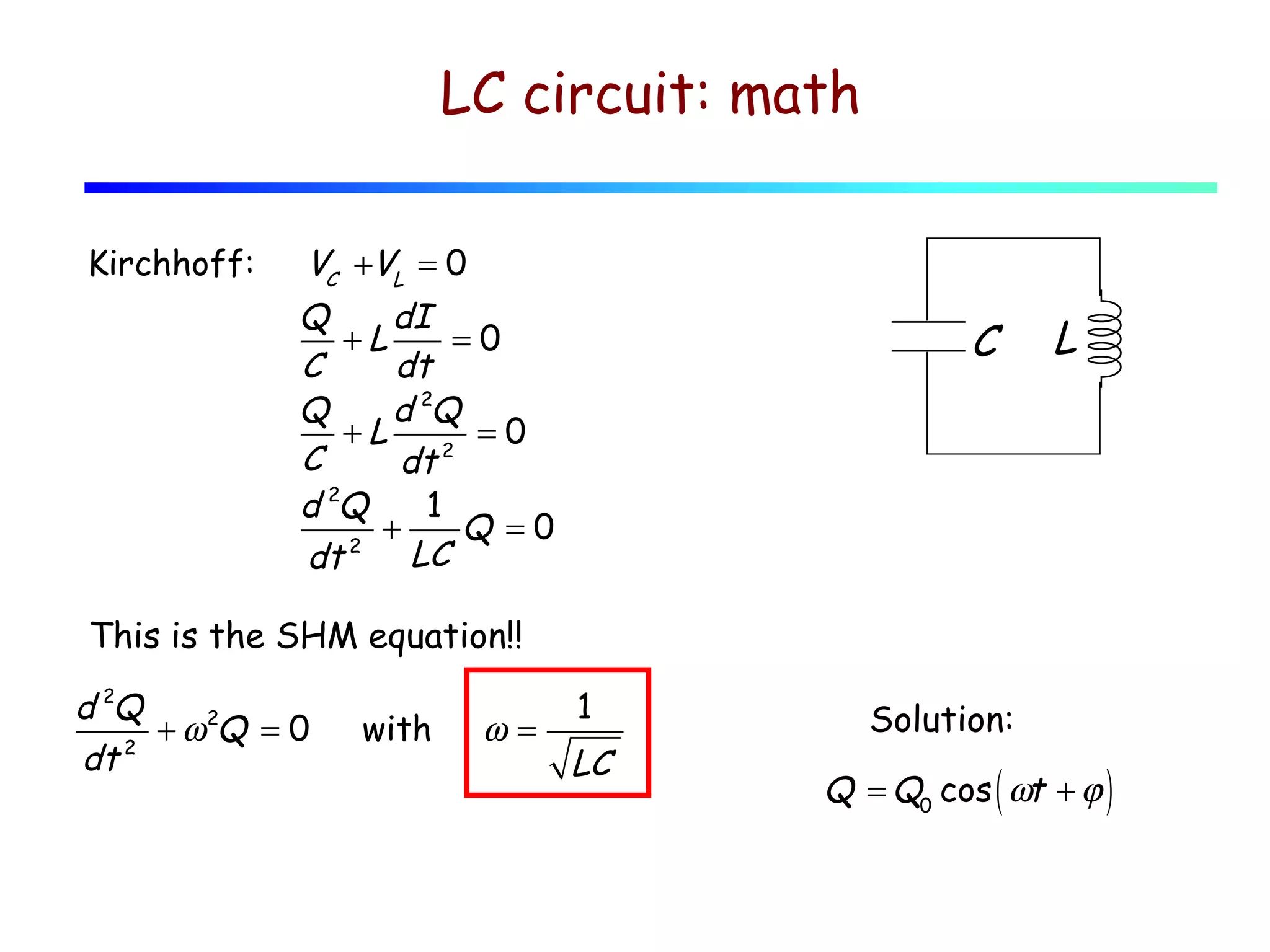
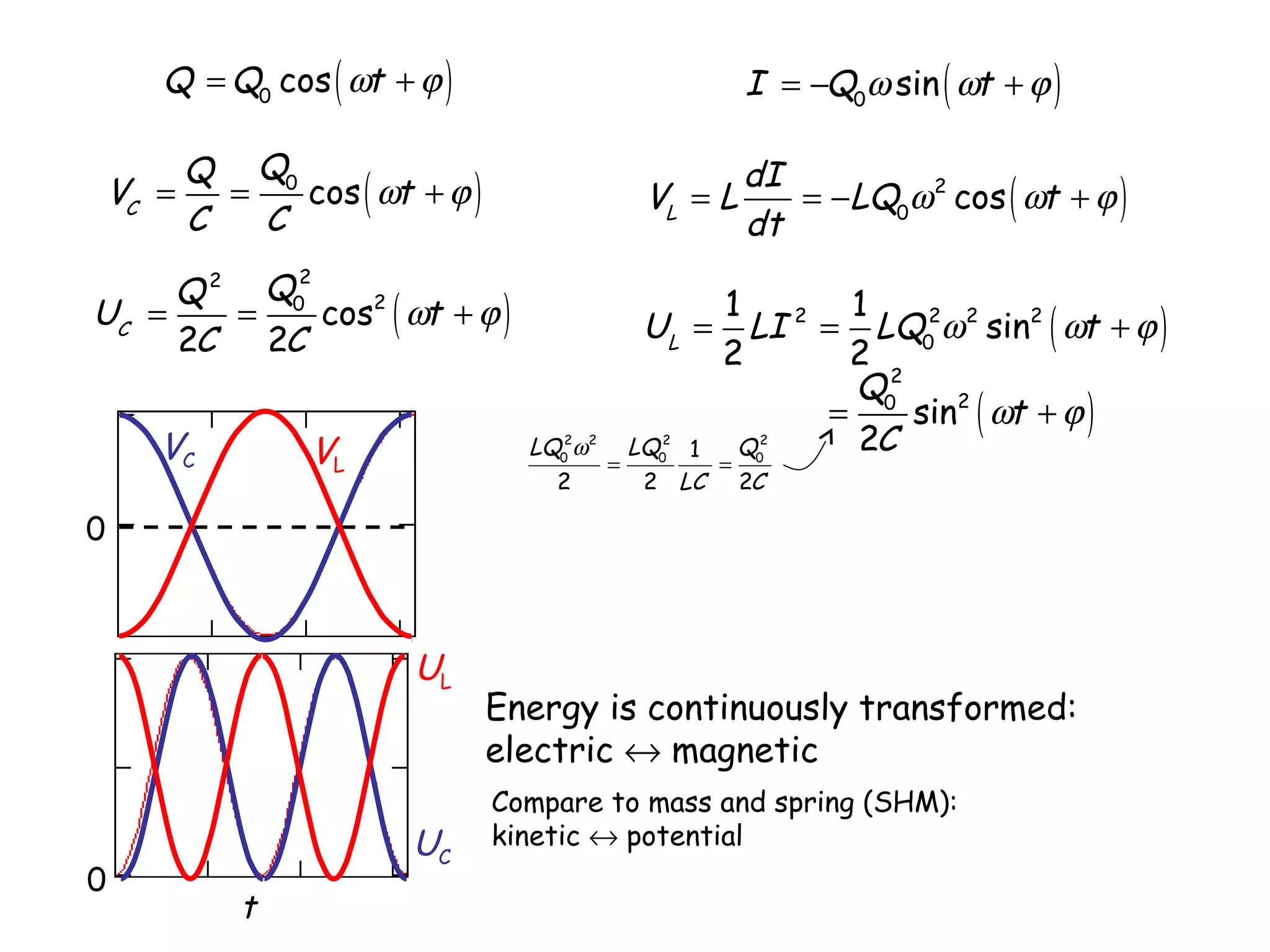
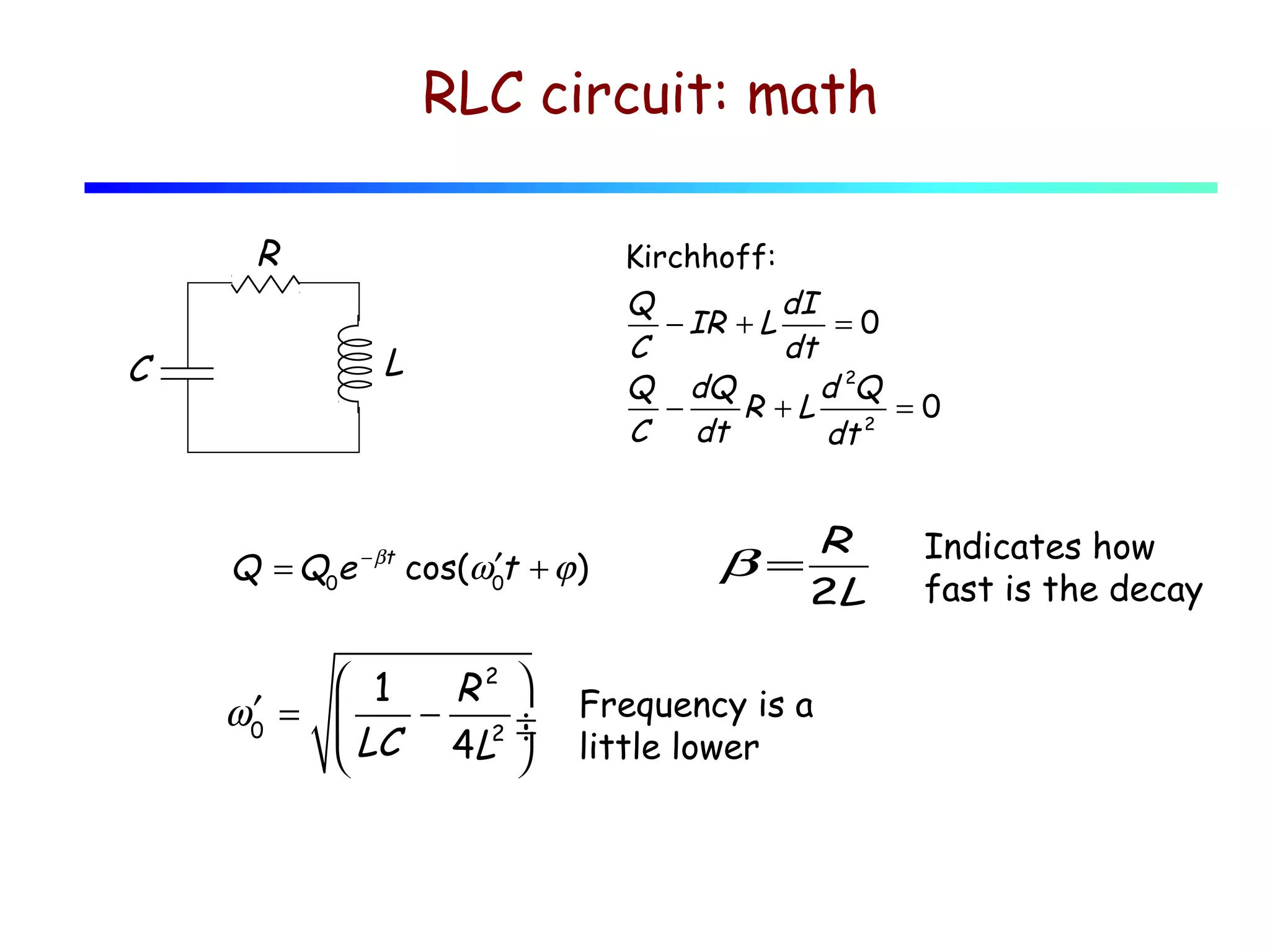
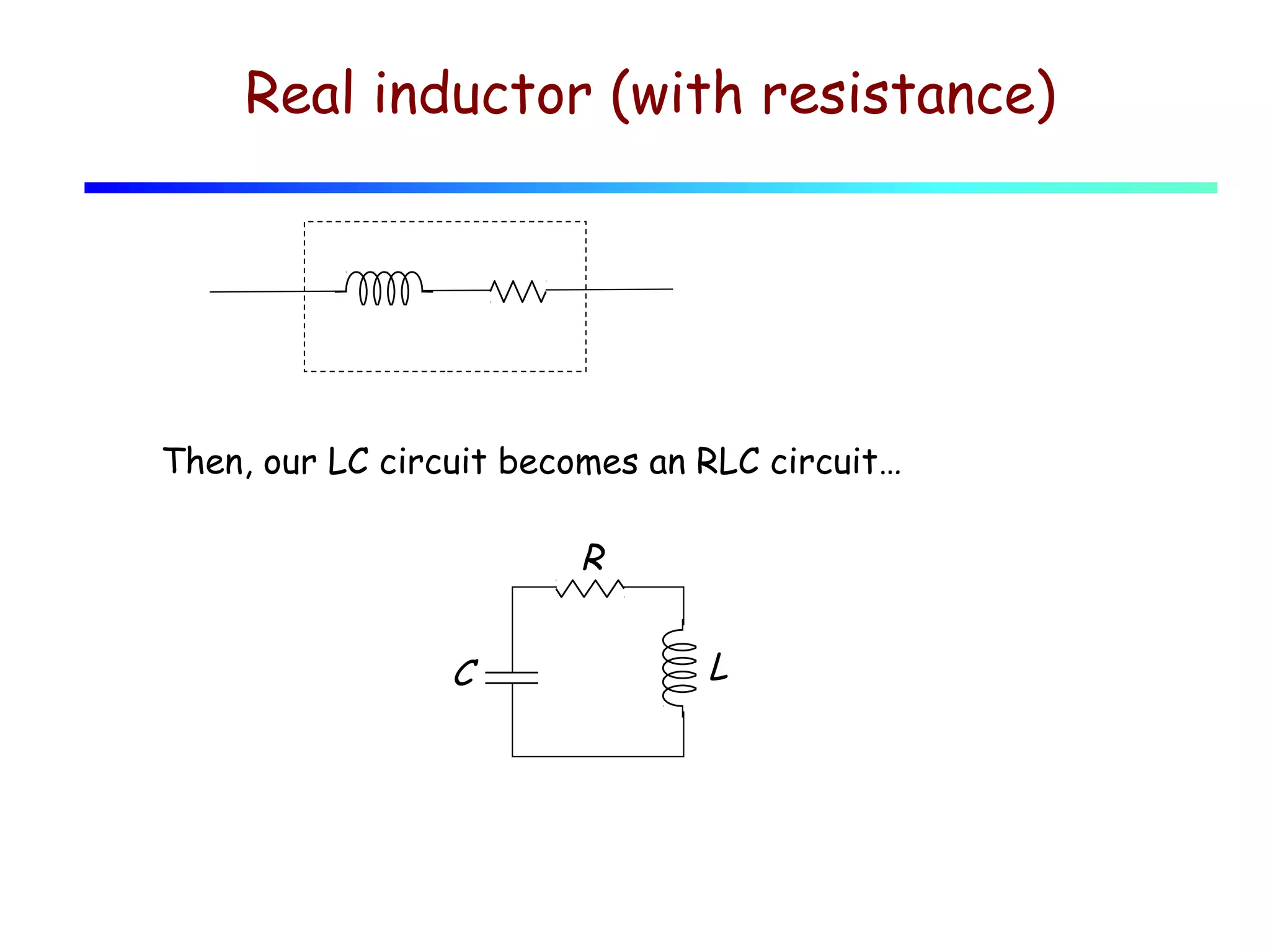
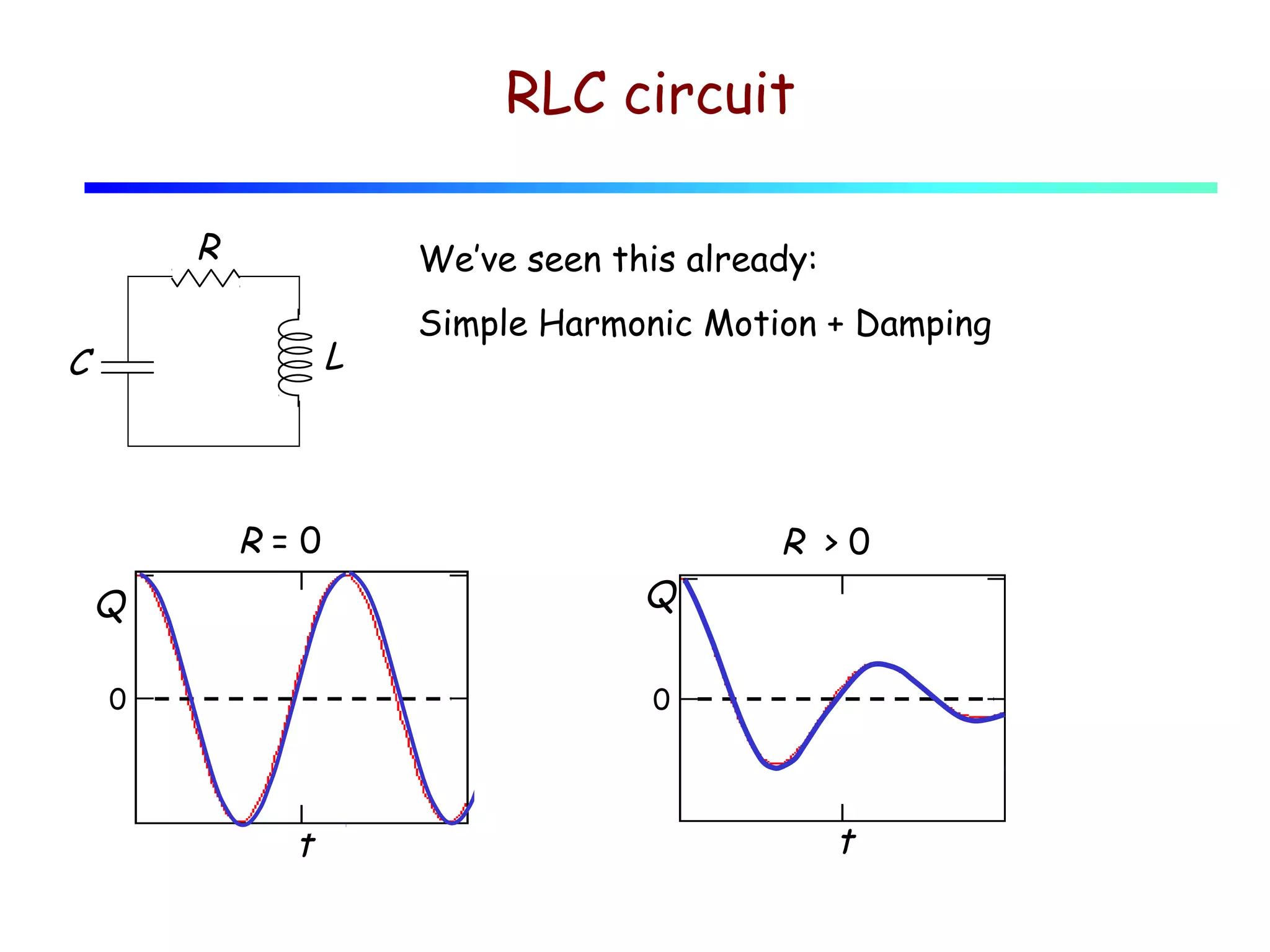
1) This lecture discusses energy storage in capacitors and inductors, as well as RC, RL, LC, and RLC circuits. 2) In an LC circuit without resistance, the charge oscillates back and forth between the capacitor and inductor at the characteristic frequency. 3) When resistance is added to an RLC circuit, the charge still oscillates but decays exponentially over time, governed by the damping ratio.

1. Lecture 28
LC and RLC circuits.

2. Energy in E and B fields
Energy stored in a capacitor
1
U = CV 2
2
++++++
−−−−−−
E
→ energy of the electric field
Energy stored in a inductor
U =
1
LI 2
2
B
→ energy of the magnetic field

3. RC circuits (review)
Capacitor is initially charged with Q0. What happens when switch is closed?
++
C −−
( )
+
Current starts at I 0 =
R
Q0 −t
e τ
And then decays: I ( t ) =
RC
I
Q
Q0
RC
t
τ = RC
U
2
Q0
2C
Q0
Current through R
VC
Q
= 0
R RC
t
Charge in capacitor
t
Energy in
capacitor

4. RL circuit
Capacitor is initially charged with Q0. What happens when switch is closed?
++
C −−
L
• Right after it is closed: I = 0. Then
current builds up.
• Magnetic field is created in inductor
while charge in capacitor is decreasing
• Energy is being transferred form C to L
(from electric to magnetic energy)
As C discharges, current should decrease and stop, but inductor keeps it
going, so at the end the capacitor is charged again but with the positive
charge on the bottom plate.
Then we start all over again…
→ Oscillatory system
Note: No dissipation mechanism (no R) ⇒ total energy is constant

5. I=0
Q = Q0
++++
E
C
----
I = I0
Q=0
L
⇒
I=0
I = -I0
C
B
⇓
⇑
Q=0
L
C
L
⇐
B
Q = -Q0
---E
C
++++
L

6. ACT: LC circuit
At t =0, the capacitor in the LC circuit shown has a total charge Q0. At t =
t1, the capacitor is uncharged. What is the sign of Vb-Va, the voltage across
the inductor at time t1?
A. Vb-Va > 0
B. Vb-Va = 0
C. Vb-Va < 0
Q = 0 ⇒ VC = 0
But VC = −VL at all times!
++++
----
C
L
•a
•b
So at t =t1, VL = 0
Compare the energy stored in the capacitor and the inductor at time t1:
A. UC < UL
B. UC = UL
C. UC > UL
Q = 0 ⇒ UC = 0
UL is then maximum.

7. LC circuit: math
Kirchhoff:
VC +VL = 0
Q
dI
+L
=0
C
dt
Q
d 2Q
+L
=0
2
C
dt
d 2Q
1
+
Q =0
2
LC
dt
C
L
This is the SHM equation!!
d 2Q
+ ω 2Q = 0
dt 2
with
ω=
1
LC
Solution:
Q = Q0 cos ( ωt + ϕ )

8. Q = Q0 cos ( ωt + ϕ )
VC =
I = −Q0ω sin ( ωt + ϕ )
Q Q0
=
cos ( ωt + ϕ )
C
C
VL = L
2
Q 2 Q0
UC =
=
cos2 ( ωt + ϕ )
2C
2C
VC
VL
UL =
dI
= −LQ0ω 2 cos ( ωt + ϕ )
dt
1
1
LI 2 = LQ02ω 2 sin2 ( ωt + ϕ )
2
2
Q02
=
sin2 ( ωt + ϕ )
2C
Q
2
LQ02ω 2 LQ02 1
=
= 0
2
2 LC 2C
0
UL
0
UC
t
Energy is continuously transformed:
electric ↔ magnetic
Compare to mass and spring (SHM):
kinetic ↔ potential

9. Real inductor (with resistance)
Then, our LC circuit becomes an RLC circuit…
R
C
L

10. RLC circuit
R
We’ve seen this already:
L
C
Simple Harmonic Motion + Damping
R=0
R >0
Q
Q
0
0
t
t

11. RLC circuit: math
R
Kirchhoff:
Q
dI
− IR + L
=0
C
dt
Q dQ
d 2Q
−
R +L
=0
C dt
dt 2
L
C
Q = Q0e
− βt
′
cos(ω0t + ϕ )
 1
R2 
′
ω0 = 
 LC − 4L2 ÷
÷


β=
R
2L
Frequency is a
little lower
Indicates how
fast is the decay