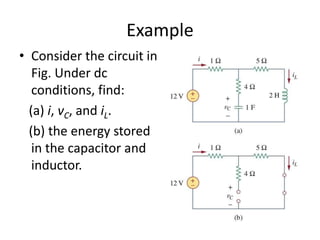
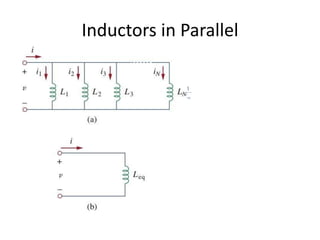
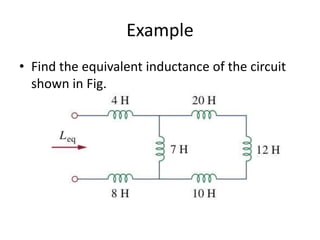
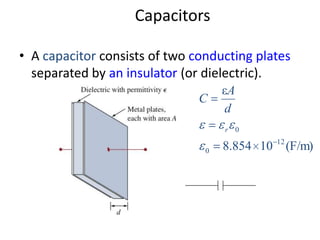
Capacitors and inductors are passive circuit elements that can store energy. - Capacitors store energy in an electric field between conducting plates separated by an insulator. The capacitance is affected by the area of the plates, distance between plates, and the material between the plates. - Inductors store energy in a magnetic field created by current through a coil of wire. The inductance depends on the number of wire turns, length of the coil, and material inside the coil. 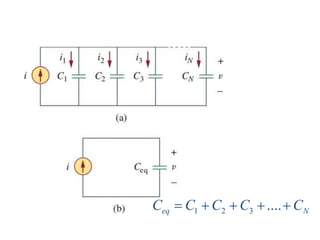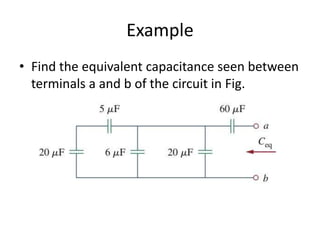- Capacitors and inductors have characteristic equations relating voltage, current, charge, and energy that make them useful for circuit analysis. Their properties allow them to be combined in series and parallel configurations.

1. Capacitors and Inductors
•
•
•
•
•
Introduction
Capacitors
Series and Parallel Capacitors
Inductors
Series and Parallel Inductors
1

2. Introduction
•
•
Resistor: a passive element which dissipates
energy only
Two important passive linear circuit
elements:
1) Capacitor
2) Inductor
•
Capacitors and inductors can store energy
only and they can neither generate nor
dissipate energy.
2

3. Capacitors
• A capacitor consists of two conducting plates
separated by an insulator (or dielectric).
C
εA
d
r 0
0
8.854 10
12
(F/m)

4. •
εA
C
d
Three factors affecting the value of
capacitance:
1. Area: the larger the area, the greater the
capacitance.
2. Spacing between the plates: the smaller the
spacing, the greater the capacitance.
3. Material permittivity: the higher the
permittivity, the greater the capacitance.

5. (a) Polyester capacitor, (b) Ceramic capacitor, (c) Electrolytic capacitor

7. Charge in Capacitors
• The relation between the charge in plates and
the voltage across a capacitor is given below.
q Cv
q
Linear
Nonlinear
1F 1 C/V
v

8. Voltage Limit on a Capacitor
• Since q=Cv, the plate charge increases as the
voltage increases. The electric field intensity
between two plates increases. If the voltage
across the capacitor is so large that the field
intensity is large enough to break down the
insulation of the dielectric, the capacitor is out
of work. Hence, every practical capacitor has a
maximum limit on its operating voltage.

9. I-V Relation of Capacitor
dv
i C
dt
+
v
i
C
-
• when v is a constant voltage, then i=0; a constant
voltage across a capacitor creates no current through
the capacitor, the capacitor in this case is the same as
an open circuit.

10. Conversion from i to v
dv
i C
dt
+
v(t )
1
C
t
idt
v
-
v(t )
1
C
t
to
idt v(to)
i
C

11. Energy Storing in Capacitor
p
w
dv
Cv
dt
vi
t
pdt C
w(t )
t
dv
v dt C
dt
v (t )
v(
1
2
Cv (t )
2
1 2
vdv
Cv
)
2
+
v
-
i
C
v (t )
v( )

12. Example
(a) Calculate the charge stored on a 3-pF
capacitor with 20V across it.
(b) Find the energy stored in the capacitor.
q Cv,
w(t )
1
Cv 2 (t )
2

13. Example
Solution:
(a) Since q Cv,
q 3 10
12
20 60pC
(b) The energy stored is
1 2
w
Cv
2
1
12
3 10
400 600pJ
2

14. Example
• Obtain the energy stored in each capacitor
under dc condition.

15. Example
Solution:
• Under dc condition, we replace each capacitor
with an open circuit. By current division,
3
i
(6mA) 2mA
3 2 4
v1 2000 i 4 V, v 2 4000i 8 V
1
1
2
3
2
w1
C1v1
(2 10 )(4) 16mJ
2
2
1
1
2
3
2
w2
C2v2
(4 10 )(8) 128mJ
2
2

16. Ceq
C1 C2 C3 .... C N
Ceq
C1 C2 C3 .... CN

17. 1
Ceq
1
C1
1
C2
1
C3
...
1
CN
1
Ceq
1
C1
1
C2

18. Example
• Find the equivalent capacitance seen between
terminals a and b of the circuit in Fig.

19. Example
Solution:
20
F and 5
F capacitors are in series :
20 5
4 F
20 5
4
F capacitor is in parallel with the 6
F
and 20
F capacitors :
4 6 20 30 F
30
F capacitor is in series with
the 60
F capacitor.
30 60
Ceq
F 20 F
30 60

20. Example
• The voltage across a 5- F capacitor is
v(t ) 10 cos 6000t V
dv
i C
dt
Calculate the current through it.
Solution:
• By definition, the current is
i
dv
C
dt
5 10
d
5 10
(10 cos 6000t )
dt
6
6
6000 10 sin 6000t
0.3 sin 6000t A

21. Example
• Determine the voltage across a 2- F capacitor
if the current through it is
3000t
i (t ) 6e
mA
Assume that the initial capacitor voltage is
zero.
1 t
Solution: v
idt v(0) and v(0) 0,
0
C
• Since
t
1
3000 t
3 103 3000 t t
3
v
6e
dt 10
e
6 0
0
2 10
3000
(1 e 3000t )V

22. Capacitor Rules and Equations
• For capacitors, we have the
following rules and equations
which hold:
q Cv,
w(t )
1
2
Cv (t )
2
dv
i C
dt
1 t
v
idt v(0)
0
C
CX = #[F]
+ vC
iC

23. Why do we cover inductors?
Aren’t capacitors good enough for
everything?
• This is a good question. Capacitors, for practical
reasons, are closer to ideal in their behavior than inductors.
In addition, it is easier to place capacitors in integrated
circuits, than it is to use inductors. Therefore, we see
capacitors being used far more often than we see inductors
being used.
• Still, there are some applications where inductors simply
must be used. Transformers are a case in point. When we
find these applications, we should be ready, so that we can
handle inductors.

24. Inductors
• An inductor is made of a coil of conducting
wire
2
N A
L
l

25. N2 A
l
L
r
0
(a) air-core
(b) iron-core
(c) variable iron-core
4
0
10 7 (H/m)
N : number of turns.
l : length.
A:cross sectional area.
: permeabili ty of the core

26. Energy Storage Form
• An inductor is a passive element designed to
store energy in the magnetic field while a
capacitor stores energy in the electric field.
v
d
dt
di
L
dt
• When the current through an inductor is a
constant, then the voltage across the inductor
is zero, same as a short circuit.

27. Formulae for Inductors
+
v
d
dt
i
1
L
w(t )
di
L
dt
t
to
v
L
-
v(t )dt i(to)
1 2
Li (t )
2

28. Example
• The current through a 0.1-H inductor is
i(t) = 10te-5t A. Find the voltage across the
inductor and the energy stored in it.
Solution:
di
Since v L and L 0.1H,
dt
d
5t
5t
5t
5t
v 0.1 (10te ) e
t ( 5)e
e (1 5t )V
dt
The energy stored is
1 2 1
2 10 t
2 10 t
w
Li
(0.1)100t e
5t e J
2
2

29. Example
• Find the current through a 5-H inductor if the
voltage across it is
2
30t , t 0
v(t )
0,
t 0
Also find the energy stored within 0 < t < 5s.
Assume i(0)=0.
1 t
v(t )dt i (t0 ) and L 5H.
Solution: Since i
Lt
t
t3
1
2t 3 A
i
30t 2 dt 0 6
3
50
0

30. The power p
vi
Example
5
60t , and the energy stored is then
6
t 5
w
pdt 0 60t dt 60
156.25 kJ
60
Alternativ ely, we can obtain the energy stored using
5
w(5) w(0)
5
1 2
1
Li (5)
Li (0)
2
2
1
(5)(2 53 ) 2 0 156.25 kJ
2
as obtained before.

31. Example
• Consider the circuit in
Fig. Under dc
conditions, find:
(a) i, vC, and iL.
(b) the energy stored
in the capacitor and
inductor.

32. Example
Solution:
(a) Under dc condition : capacitor
open circuit
inductor short circuit
12
i iL
2 A, vc 5i 10 V
1 5
(b)
wc
wL
1
1
2
Cvc
(1)(10 ) 50J,
2
2
1 2 1
Li
(2)(22 ) 4J
2
2
2

33. Inductors in Series
Leq
L1
L2
Leq
L3 ... LN
L1
L2
L3 ... LN

34. Inductors in Parallel
1
Leq
1
L1
1
1

L2
LN

35. Example
• Find the equivalent inductance of the circuit
shown in Fig.

36. Example
• Solution:
Series : 20H, 12H, 10H
42H
7 42
6H
Parallel :
7 42
Leq 4 6 8 18H