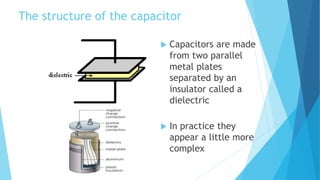
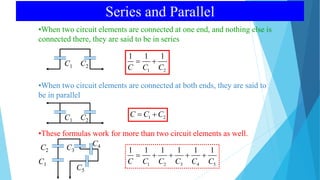
Capacitors store electric charge and are made of two conducting plates separated by an insulating material. They have many applications including in electronics like cameras and power surge protectors. The amount of charge a capacitor can store is proportional to the voltage across its plates and depends on factors like the plate area, distance between plates, and the insulating material. Capacitors can be connected in series or parallel in circuits. In series, the capacitance is the reciprocal of the sum of the reciprocals of the individual capacitances. In parallel, the total capacitance is the sum of the individual capacitances.

1. Capacitors
Qafqaz Univeristeti:
Fizika muəllimliyi(eng):
Səid Paşayev

2. What is capacitor??????
Anyone can say???
Yes we are listening to you…

3. Capacitors
• Capacitors have many
applications:
– Computer RAM memory and
keyboards.
– Electronic flashes for cameras.
– Electric power surge protectors.
– Radios and electronic circuits.

4. Electronic Components
 Capacitors are
electronic components
that store charge
efficiently
 They can be charged
and discharged very
quickly and hold their
charge indefinitely
 Symbol

5. The structure of the capacitor
 Capacitors are made
from two parallel
metal plates
separated by an
insulator called a
dielectric
 In practice they
appear a little more
complex

6. Capacitors and Capacitance
Charge Q stored:
CVQ 
The stored charge Q is proportional to the potential
difference V between the plates. The capacitance C is
the constant of proportionality, measured in Farads.
Farad = Coulomb / Volt
A capacitor in a simple
electric circuit.

7. Capacitance (symbol C)
 Capacitance is the amount of charge a capacitor can store when
connected across a potential difference of 1V (the larger the capacitance
the more charge it can store)
 Units of capacitance are Farads (symbol F)
 1 Farad = 1 coulomb per volt This is a lot of charge!!
 most capacitors are small;
µF (1 x 10-6 F)
nF (1 x 10-9 F)
pF (1 x 10-12 F)
V
Q
C 
Where;
C=Capacitance in Farads (F)
Q=Charge in Coulombs (C)
V=Voltage in Volts(V)

8. Exercises
1. Calculate the capacitance of a capacitor that stores 1.5 
10-9C at 7.2V?

9. Capacitance (C)
Three factors determine
capacitance;
1. The area of the plates (CA)
2. The distance separating the
plates
(C  )
3. The properties of the dielectric
(εr)
so
C= constant x
d
1
d
A

10.  If there is air or a vacuum between the plates the
constant is;
the absolute permittivity of free space (symbol ε0)
(ε0 = 8.84 x 10-12 Fm-1)
so;
d
A
C 0

Capacitor Construction Formula

11.  When an insulator (dielectric) is placed between
the plates the capacitance increases
 The dielectric constant (symbol εr) gives the
proportion by which the capacitance will increase
so;
and therefore
Note that εr has no units as
d
A
C or


airrdielectic
CC  
air
dielectric
r
C
C

Insulator εr
Air 1
Polystyrene 2.5
Glass 6.0
Water 80
Capacitor Construction Formula

12. 1-PLATE AREA: All other factors being equal, greater
plate area gives greater capacitance; less plate area
gives less capacitance.
2-PLATE SPACING:
All other factors being equal, further plate spacing
gives less capacitance; closer plate spacing gives
greater capacitance.

13. 3-DIELECTRIC MATERIAL: All other factors being
equal, greater permittivity of the dielectric gives
greater capacitance; less permittivity of the
dielectric gives less capacitance.

14. Examples
1. Calculate the capacitance of a capacitor with a
polystyrene dielectric (εr =2.5), an area of 1.2cm
by 3.2m and a plate separation of 8
micrometers.
d
A
C or


(ε0 = 8.84 x 10-12 Fm-1)

15. Combination of
capacitors

16. Capacitors in Parallel
V C1 C2
Q C V 
•When capacitors are joined at both ends like
this, they are said to be in parallel
•They have the same voltage across them
•They can be treated like a single capacitor:
1 1
2 2
Q C V
Q C V
 
  1 2Q Q Q   1 2C C V   1 2C C C 
•When capacitors are joined at one end, with
nothing else, they are said to be in series
•They have the same voltage across them
•They can be treated like a single capacitor:
V C
1C
2
1 1
2 2
Q C V
Q C V
 
  1 2
Q Q
C C
 1 2V V V    
Q
C

1 2
1 1 1
C C C
 
Capacitors in Series

17. Series and Parallel
•When two circuit elements are connected at one end, and nothing else is
connected there, they are said to be in series
1 2
1 1 1
C C C
 
•When two circuit elements are connected at both ends, they are said to
be in parallel
1 2C C C 
C1 C2
C1 C2
•These formulas work for more than two circuit elements as well.
C1
C2 C3
C4
C5
1 2 3 4 5
1 1 1 1 1 1
C C C C C C
    

18. Examples
1. A circuit has three 330 μF capacitors in
series. Calculate the total capacitance of the
circuit
2. Another circuit has three 330 μF
capacitors in parallel. Calculate the total
capacitance of the circuit.

19. • Find the equivalent capacitance seen
between terminals a and b of the circuit
in Figure.

20. Solution:
:seriesinarecapacitorsF5andF20  
F4
520
520




F6with theparalleliniscapacitorF4  
:capacitorsF20and 
F302064 
withseriesiniscapacitorF30 
capacitor.F60the 
F20F
6030
6030
 


eqC

21. Problems solve at home:
1. A 330μF capacitor is charged by a 9.0V battery. How
much charge will it store?
2. A 0.1μF capacitor stores 1.5  10-7 C of the charge.
What was the voltage used to charge it?
3. Calculate the plate area required for a 1000 μF, glass
(εr=6.0) capacitor, with a plate separation of 2.8
micrometres.
4. Calculate the dielectic constant of a 10000 μF
capacitor with a 1.2μm plate separation and an area
of 16.97m2

22. Calculate effective capacitance:
a b
15 μF 3 μF
6 μF
What is the effective capacitance Cab between points a and b?
20 μF
C1 C2
C3
C4
Cab
?