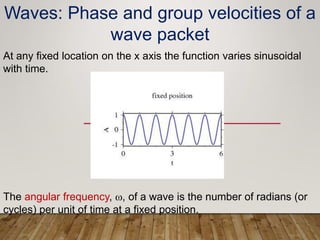
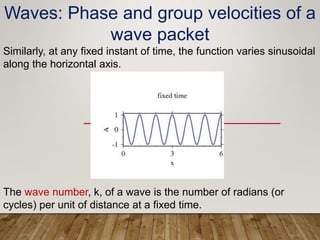
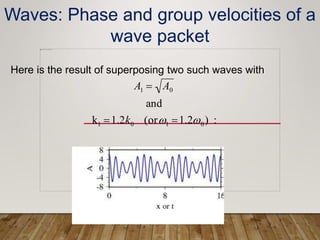
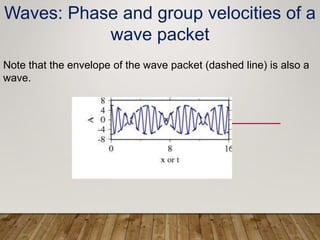
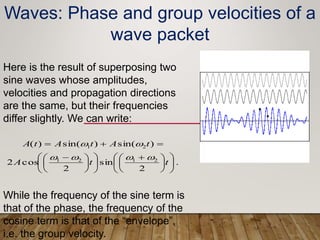
The document discusses phase and group velocity of waves. It defines phase velocity as the velocity at which the phase of any single frequency component travels, represented by the crests of a wave. Group velocity is defined as the velocity at which the envelope or outline of a wave packet travels through space. The document demonstrates through equations and diagrams that for wave packets formed from superimposed waves, the phase velocity can be greater than the group velocity.

1. Group
velocity and
phase
velocity
Dr. R. M. Thombre
HOD Dept. of Physics
M. G. College Armori

2. Waves: Phase and group velocities of a
wave packet
The velocity of a wave can be defined in many different ways,
partly because there are different kinds of waves, and partly
because we can focus on different aspects or components of any
given wave.
The wave function depends on both time, t, and position, x, i.e.:
where A is the amplitude.

A A(x,t) ,

3. Waves: Phase and group velocities of a
wave packet
At any fixed location on the x axis the function varies sinusoidal
with time.
The angular frequency, , of a wave is the number of radians (or
cycles) per unit of time at a fixed position.

4. Similarly, at any fixed instant of time, the function varies sinusoidal
along the horizontal axis.
The wave number, k, of a wave is the number of radians (or
cycles) per unit of distance at a fixed time.
Waves: Phase and group velocities of a
wave packet

5. A pure traveling wave is a function of w and k as follows:
where A0 is the maximum amplitude.
A wave packet is formed from the superposition of several such
waves, with different A, , and k:

A(t,x)  A0 sin(t  kx) ,
A(t,x)  An sin(nt  kn x)
n
 .
Waves: Phase and group velocities of a
wave packet

6. Here is the result of superposing two such waves with

A1  A0
and
k1 1.2k0 (or1 1.20) :
Waves: Phase and group velocities of a
wave packet

7. Note that the envelope of the wave packet (dashed line) is also a
wave.
Waves: Phase and group velocities of a
wave packet

8. Here is the result of superposing two
sine waves whose amplitudes,
velocities and propagation directions
are the same, but their frequencies
differ slightly. We can write:
While the frequency of the sine term is
that of the phase, the frequency of the
cosine term is that of the “envelope”,
i.e. the group velocity.
.
2
sin
2
cos
2
)
sin(
)
sin(
)
(
2
1
2
1
2
1











 











 



t
t
A
t
A
t
A
t
A






Waves: Phase and group velocities of a
wave packet

9. The speed at which a given phase propagates does not coincide
with the speed of the envelope.
Note that the phase velocity is
greater than the group velocity.
Waves: Phase and group velocities of a
wave packet

10. The group velocity is the velocity with which the envelope of the
wave packet, propagates through space.
The phase velocity is the velocity at which the phase of any one
frequency component of the wave will propagate. You could pick
one particular phase of the wave (for example the crest) and it
would appear to travel at the phase velocity.
Waves: Phase and group velocities of a
wave packet